
Everyday we spend a large part of our time waiting for one thing or another. We wait to get bread at the bakery every morning. We wait every time we go to see our doctors. We wait to reach our destination during a taxi ride, or for our contacts to respond in our social networks. And waiting isn’t exclusive to us. The jobs we run on our computers wait to be processed just as new laws and regulations wait to be approved.
Naturally, we want to spend as little time as possible waiting. And the systems providing the things for which we wait usually try to minimise the amount of time they keep us waiting too. What is clear is that it can be extremely valuable to know, for both parties, how long a given situation is more or less going to last. With such information one can plan ahead, and service providers can optimise their processes.
A glance at Queuing Theory
There is a branch of Mathematics called “Queuing Theory” that precisely studies waiting times and queues, in order to predict how long one will wait for a given service. Let’s set some of its terminology first. As hinted above, every queue has two components: the job or client waiting and the system dealing with the client (aka the service provider). To predict how long a client will wait, one needs to first predict when she’s arriving (aka the arrival time) and then, conditioned on the arrival time, predict how long the system will take in finishing its service (aka the service time).
Imagine you are in the waiting room of your doctor’s office. To kill the time, you decide that you want to predict whether a new patient is about to arrive at the office, right at the moment you are staring at the door. There are many factors you can’t possibly know that influence whether one person, let’s call her Sarah, is going to arrive at that precise instant. She may have missed that train she needed to catch or run into that old friend who chats a bit too much. The best you can do in such a scenario is to assign a probability to her arriving in say, the next sixty seconds. Likewise, you can only assign a probability to the doctor spending exactly fifteen minutes with Sarah once her turn is up. And here again, this last probability must clearly depend on her arrival time.
Mathematicians and statisticians together have built many statistical models predicting such kinds of probabilities. These models, however, usually make strong assumptions about either the nature of client arrival process (as e.g. there’s on average one client arriving every half an hour) or the service provider (as e.g. clients are served one at a time, in the order in which they arrive) or both. In practice, these assumptions are either too rough to describe how things actually happen, or way too specific to some class of service systems.
Generating service times with GANs
Instead of estimating probabilities we propose to directly generate random numbers, according to the probability distribution underlying a dataset of recorded service times. If chosen appropriately, these random numbers can correspond to our service time predictions. Let’s explain:
Suppose you have a large dataset of recorded arrival and service times, for a given service provider. Similar to what we argued above, such recordings don’t give a complete picture of either the arrival or the service process involved. Thus, we again resort to specifying our uncertainty about these processes in terms of unknown probability distributions, which simply are functions giving the probabilities for our arrival and departure events. Now, one way to implicitly infer the service time probability distribution is to choose a random number generator, sample random numbers from it and input them into a deep neural network. The neural network can then be trained so that the probability distribution of its random outputs matches, in some way or another, the probability distribution underlying the recorded (i.e. real) service times. Generative Adversarial Networks (GANs) do precisely this by minimising some notion of dissimilarity between the real and the artificial distributions. This notion of dissimilarity in GANs is modelled with a neural network too, usually known as critic or discriminator, in the Machine Learning literature, whereas the neural network of random numbers is typically called the generator.
Inferring conditional service time distributions
There is however a challenge that remains, namely how do you sample service times conditioned on the arrival times? We have solved this problem by splitting it into two parts. First, we use a class of recurrent neural networks specifically designed to learn representations of the arrival process. These representations are nothing but a reformulation of the arrival times that better summarise the history of arrivals. We then input these representations into both the generator (together with the random numbers) and critic (together with our predictions) of the GAN. As a result, our generator learns how to sample from a service time distribution, conditioned on the continuous-time arrival process. We encourage you to read our AAAI paper for the details.
The usefulness of this approach is that we don’t need to assume anything about the actual service systems we want to analyse. All we need is the arrival and service times.
Modelling real-world service providers
We have used this idea to learn the service time distributions of three very different service providers, namely Github (a version control repository), Stack Overflow (a question-answering platform for programmers) and the New York City (NYC) Taxi network. Figure 1 shows histograms of the empirical service time distributions of these providers (blue points), sampled from our test set, against those we generated (yellow points).
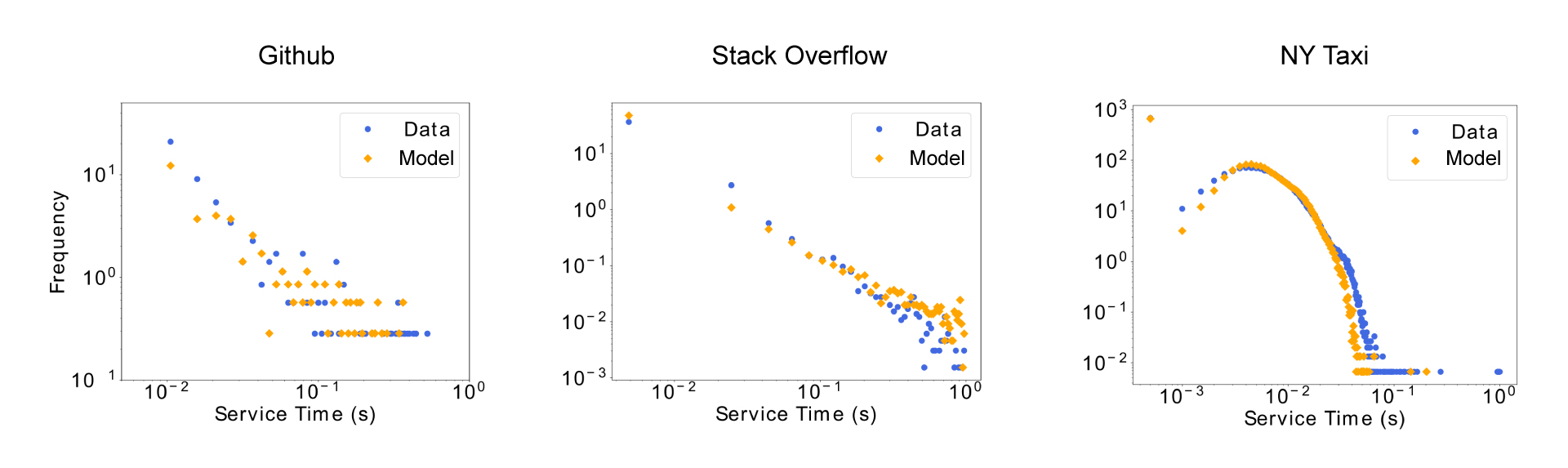
Note how the model captures both long- and short-term behaviour in all systems. The agreement is remarkable. And, very importantly, our model allows us to predict new service times. You only need to input the arrival time of a new event and it will output how long the service will last.
Further information in the respective paper:
Learning Deep Generative Models für Queuing Systems
Cesar Ojeda, Kostadin Cvejoski, Bogdan Georgiev, Christian Bauckhage, Jannis Schuecker, Ramses Sanchez (Proceedings of the AAAI Conference on Artificial Intelligence), 2021, PDF.
