
Quantum Computing (QC) has ushered in a new era of computation, promising to solve problems that are practically infeasible for classical computers. One of the most exciting applications of quantum computing is its ability of solving combinatorial optimization problems, such as Quadratic Unconstrained Binary Optimization (QUBO). This problem class has regained significant attention with the advent of Quantum Computing. These hard-to-solve combinatorial problems appear in many different domains, including finance, logistics, Machine Learning and Data Mining. For more details on QC and optimization in Machine Learning, we refer to our blog entries “Quantum computers: new potential for machine learning (in german)” and “Optimization in Machine Learning (in german)”.
To harness the power of Quantum Computing for QUBO, we introduce qubolite, a Python package comprising utilities for creating, analyzing, and solving QUBO instances, which incorporates current research algorithms developed by scientists at the Lamarr Institute.
Understanding QUBO: Optimization of Binary Variables
Before we dive into qubolite, let us understand what QUBO is. As the name already indicates, we are concerned with the problem of finding binary values that optimize a quadratic objective function. Mathematically, this problem can be expressed as:
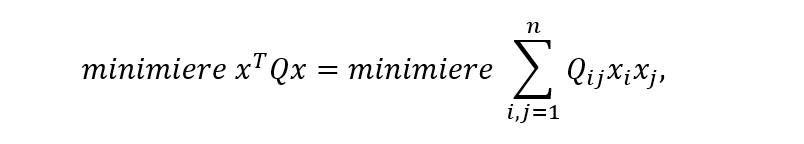
where x is a binary vector and Q is a symmetric matrix, encoding the problem’s parameters.
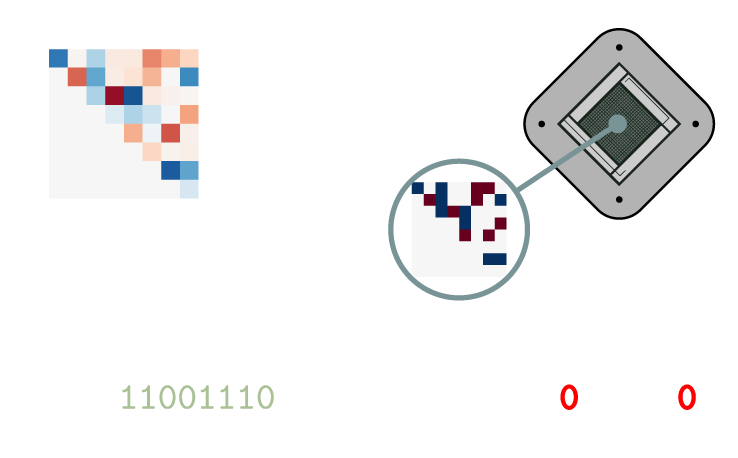
Through their discrete nature, instances of QUBO arise mainly in the domain of combinatorial optimization, that is, where we want to find an optimal configuration of variables among a finite number of possibilities. However, such problems are often hard or even intractable to solve with classical computers, since the number of possible solutions grows exponentially with the problem dimension, i.e., the number of variables. Quantum Computing can potentially offer significant speedup in solving QUBO problems, thanks to algorithms like Quantum Approximate Optimization Algorithm (QAOA) and Quantum Annealing. However, since today’s quantum hardware is very prone to errors and limited in computing power, one has to be very careful in designing suitable problem formulations which can be solved with the quantum resources available to us. Integrated control errors are a prominent example of these limitations, which describe the physical errors appearing when implementing a given QUBO problem on the hardware. During this process, parameters can be altered, which then leads the quantum annealer to solve a different problem, obtaining sub-optimal solutions of the original problem. This effect is visualized in Fig. 1.
Unlocking QUBO: Introducing qubolite
To make working with QUBO more accessible, scientists at the Lamarr Institute have developed qubolite, a comprehensive Python package which provides a range of utilities:
- QUBO utilities: Many utilities which are useful when working with QUBO are integrated, such as easy instantiation, conversion to and from the Ising model, computing the parameters’ dynamic range, sampling, or partial assignments of certain variables.
- Problem solvers: The package provides state-of-the-art solvers such as simulated annealing, but also a brute-force solver, with an efficient, parallelized implementation in C/C++.
- Pre-processing: To get the most out of the available solvers, methods for pre-processing are implemented. They can either identify certain properties of solutions and reduce the size of the search space, or optimally condition QUBO instances for use on real quantum computers.
- QUBO embeddings: Different real-life problems formulated as QUBO are provided, ranging from Machine Learning problems, such as clustering, to general combinatorial problems.
Getting started with qubolite
To get started with qubolite, you can install the package using pip:

We use all optional dependencies here, relying on multiple open-source python packages, such as sklearn and igraph. The default version does only depend on the numpy package. After the installation we can instantiate QUBO problems. To this end, we consider a simple clustering problem, which is generated using the Machine Learning package sklearn:

This data set is visualized in Fig. 2 (left). The goal now is to separate this data set into two clusters. We can import the clustering embedding and obtain a QUBO instance as follows:

The solution of this QUBO problem represents a perfect clustering of the dataset. Since our problem size here is rather small (30), we can use a brute-force approach, which rates the quality of every possible solution and returns the best one.

The obtained solution is visualized in Fig. 2 (right), indicating the cluster assignments with different colors. Of course, with an increasing size of our data set at hand, a brute-force approach is not possible anymore, since the number of solutions grows exponentially with the problem dimension.

Preprocessing for Quantum Computers
Since quantum computers utilize the quantum-mechanical phenomenon of superposition, they inherit the ability to search efficiently for an optimal solution in exponentially large spaces. Nowadays, quantum hardware is still in its infancy since it possesses a limited size of qubits and is prone to errors.
How strong these errors impact the solution quality is largely dependent on the dynamic range of the given QUBO matrix parameters. The dynamic range corresponds to the number of bits required to encode the QUBO parameters faithfully, considering the covered value range and small gradations. Scientists at the Lamarr Institute developed an algorithm for reducing the dynamic range of a given QUBO problem, while maintaining the optimal solution. This method is implemented in qubolite and can be used in the following way:

Not only the performance of real quantum annealers is increased by reducing the dynamic range, but also the performance of classical hardware solvers which have a limited parameter bit-precision. One such exemplary hardware solver is our IAIS Evo Annealer — more details on this technology can be found in our blog-entry “Preparing for the age of quantum with the IAIS Evo Annealer”.
Bridging the Gap: Cutting-Edge Quantum Research and Real-World Impact
qubolite opens up new possibilities for solving complex optimization problems with Quantum Computing (QC), since state-of-the-art research conducted at the Lamarr Institute is integrated in real-time. The Python package provides a user-friendly and versatile toolbox for harnessing the potential of QC. It is not only used in our pure research projects but also in various industry projects at Fraunhofer IAIS, one of the four Lamarr partner institutions. As quantum hardware continues to advance, qubolite contributes to making quantum optimization accessible and impactful in a wide range of industries, being a freely usable software package.
More information on qubolite:
https://github.com/smuecke/qubolite
Optimum-Preserving QUBO Parameter Compression
Mücke, Sascha et al., 2023, arXiv preprint, pdf
