
Wir verbringen einen Großteil unseres alltäglichen Lebens damit, auf verschiedene Dinge zu warten. Wir warten jeden Morgen bei Bäcker*innen, um unser Brot zu kaufen. Wir warten jedes Mal, wenn wir eine Arztpraxis aufsuchen. Wir warten im Taxi darauf unser Ziel zu erreichen oder auf Antworten unserer Kontakte in sozialen Netzwerken. Und Warten betrifft nicht nur uns Menschen. Die Aufträge, die wir auf unseren Computern ausführen, warten darauf, verarbeitet zu werden. Genau wie neue Gesetze und Vorschriften darauf warten, genehmigt zu werden.
Naturgemäß möchten wir so wenig Zeit wie möglich mit Warten verbringen. So verfolgen auch Dienstleistungssysteme in der Regel das Ziel unsere Wartezeit zu minimieren. Klar ist, dass es für beide Seiten extrem wertvoll sein kann, zu wissen, wie lange eine bestimmte Situation mehr oder weniger andauern wird. Denn mit solchen Informationen kann man vorausschauend planen und Dienstleister können ihre Prozesse optimieren.
Ein Blick auf die Queuing Theorie
Ein Teilgebiet der Mathematik namens „Queuing Theory” untersucht Wartezeiten und Warteschlangen mit dem Ziel, vorherzusagen, wie lange man auf eine bestimmte Dienstleistung warten wird. Lassen Sie uns einige Begriffe aus diesem Teilgebiet festlegen. Wie bereits erwähnt, hat jede Warteschlange zwei Komponenten: den wartenden Auftrag oder die wartende Kundschaft und das System, das sich um die Kundschaft kümmert (das Dienstleistungssystem). Um vorherzusagen, wie lange ein Kunde oder eine Kundin warten wird, muss man zunächst vorhersagen, wann er oder sie beziehungsweise der Auftrag beim Dienstleister ankommt (Ankunftszeit), und sodann, abhängig von der Ankunftszeit, vorhersagen, wie lange das System brauchen wird, um seinen Dienst abzuschließen (Servicezeit).
Ein Beispiel: Stellen Sie sich vor, Sie sitzen im Wartezimmer Ihrer Arztpraxis. Um sich die Zeit zu vertreiben, beschließen Sie vorherzusagen, ob ein neuer Patient oder eine neue Patientin genau in dem Moment die Praxis betreten wird, als Sie zur Tür schauen. Es gibt viele Faktoren, die Sie unmöglich wissen können, die aber beeinflussen, ob eine Person – nennen wir sie Sarah – genau in diesem Moment eintreffen wird. Sarah hat möglicherweise den Zug verpasst oder hat eine alte Bekanntschaft getroffen, die immer gerne etwas zu viel plaudert. Ihr bester Schätzansatz in einem solchen Szenario ist es, Sarahs Ankunft – sagen wir in den nächsten sechzig Sekunden – eine Wahrscheinlichkeit zuzuweisen. Zudem können Sie nur eine Wahrscheinlichkeit dafür angeben, dass Sarahs Behandlung genau fünfzehn Minuten dauern wird, wenn ihr Termin beginnt. Auch diese Wahrscheinlichkeit ist somit eindeutig von der Ankunftszeit abhängig.
Gemeinsam haben Forschende der Mathematik und Statistik eine Vielzahl statistischer Modelle entwickelt, die eben diese Wahrscheinlichkeiten vorhersagen. Die Modelle machen jedoch starke Annahmen sowohl über den Prozess der Ankunftszeit der Kundschaft (zum Beispiel, dass im Durchschnitt jede halbe Stunde eine Kundin oder ein Kunde einen Auftrag vergibt) als auch über den Prozess der Dienstleistung (zum Beispiel, dass eine Person nach der anderen bedient wird, und zwar in der Reihenfolge der Ankunftszeit). Diese Annahmen sind entweder zu grob, um tatsächliche Ablaufprozesse beschreiben, oder viel zu spezifisch auf eine bestimmte Klasse von Dienstleistungssystemen zugeschnitten.
Generierung von Servicezeiten mit GANs
Anstatt Wahrscheinlichkeiten zu schätzen, schlagen wir vor, direkt Zufallszahlen entsprechend der Wahrscheinlichkeitsverteilung eines Datensatzes mit aufgezeichneten Servicezeiten zu generieren. Bei geeigneter Wahl können diese Zufallszahlen unseren Vorhersagen für die Servicezeit entsprechen. Schauen wir genauer hin:
Wir nehmen an, dass wir einen großen Datensatz mit aufgezeichneten Ankunfts- und Servicezeiten für einen bestimmten Dienstleister haben. Wie oben beschrieben, geben solche Aufzeichnungen kein vollständiges Bild über die Ankunfts- oder Dienstleistungsprozesse ab. Daher spezifizieren wir unsere Unsicherheiten in Bezug auf die Prozesse in Form von unbekannten Wahrscheinlichkeitsverteilungen. Dies sind Funktionen, die die Wahrscheinlichkeiten für unsere Ankunfts- und Abgangsereignisse angeben. Eine Möglichkeit implizit auf die Wahrscheinlichkeitsverteilung der Servicezeiten zu schließen, besteht darin, einen Zufallsgenerator zu wählen, mit ihm Zufallszahlen zu generieren und diese in ein tiefes neuronales Netz hineinzugeben. Das neuronale Netz kann dann so trainiert werden, dass die Wahrscheinlichkeitsverteilung seiner Zufallsausgaben mit der Wahrscheinlichkeitsverteilung übereinstimmt, die den aufgezeichneten (das heißt realen) Servicezeiten zugrunde liegt. Generative Adversarial Networks (GANs) tun genau das, indem sie eine Form der Unähnlichkeit zwischen realen und künstlichen Verteilungen minimieren. Die Unähnlichkeit wird in GANs hierbei ebenfalls mit einem neuronalen Netz modelliert, das in der Literatur zum Maschinellen Lernen gewöhnlich als Diskriminator bezeichnet wird. Das neuronale Netz der Zufallszahlen wird hingegen als Generator bezeichnet.
Inferenz bedingter Servicezeitverteilungen
Es bleibt jedoch eine Herausforderung – nämlich die Frage, wie man Servicezeiten in Abhängigkeit von Ankunftszeiten ermitteln kann. Wir haben dieses Problem gelöst, indem wir es in zwei Teile aufgeteilt haben. Erstens verwenden wir eine Klasse von rekurrenten neuronalen Netzen, die speziell dafür entwickelt wurden, Darstellungen von Ankunftsprozessen zu erlernen. Diese Darstellungen sind nichts anderes als eine Umformulierung der Ankunftszeiten, die die Geschichte der Ankünfte besser zusammenfasst. Nachfolgend geben wir diese Darstellung sowohl in den Generator (zusammen mit den Zufallszahlen) als auch in den Diskriminator (zusammen mit unseren Vorhersagen) des GANs ein. Als Ergebnis lernt unser Generator, wie er aus einer Servicezeitverteilung, die durch einen kontinuierlichen zeitlichen Ankunftsprozess bedingt wird, eine Stichprobe ziehen kann. Wir empfehlen unser AAAI-Paper für weitergehende Informationen zur entwickelten Methode.
Der Nutzen unseres Ansatzes ist, dass wir keine Annahmen über die eigentlichen Dienstleistungssysteme, die wir analysieren wollen, machen müssen. Wir brauchen einzig die Ankunfts- und Servicezeiten.
Modellierung von realen Dienstleistern
Wir haben unseren maschinellen Lernansatz auf die Verteilungen der Servicezeiten von drei sehr unterschiedlichen Dienstleistern angewandt: Github (ein Versionsverwaltungs-Repository), Stack Overflow (eine Frage-Antwort-Plattform für Programmierer*innen) und das New York City (NYC) Taxinetz. Abbildung 1 zeigt Histogramme für die empirischen Verteilungen der Servicezeiten dieser Anbieter (blaue Punkte) im Vergleich zu den von uns generierten Verteilungen (gelbe Punkte).
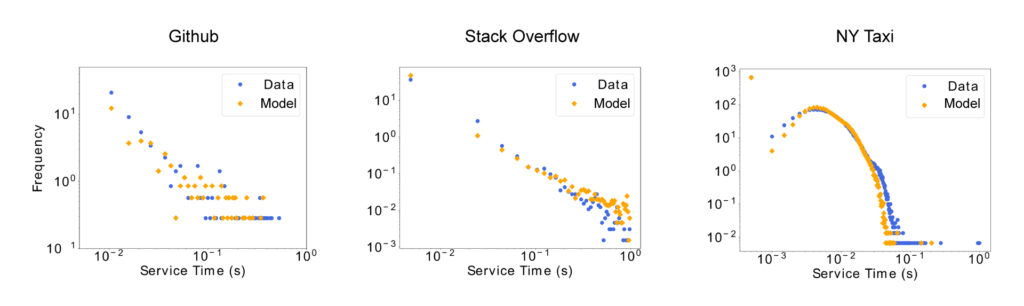
Abb. 1. Vergleich zwischen empirischen Servicezeitverteilungen von realen Dienstleistern (Testsatz) und den von unserem Modell generierten Daten. Für Github definieren wir die Erstellung von Github-Issues als Ankunft und deren Abschluss als Abgänge, so dass die Nutzer des Repository das Dienstleistungssystem darstellen. Ähnlich ist es bei Stack Overflow, hier betrachten wir das Stellen von Fragen als Ankunftszeit und die Annahme einer Antwort als Abgang, wobei die Antwortgebenden das Dienstleistungssystem darstellen. Zuletzt identifizieren wir für das NYC Taxinetz den Beginn einer Fahrt als Ankunftszeit und ihr Ende als Abgang, so dass sowohl das Taxi, das die Dienstleistung erbringt, als auch das Verkehrsnetz von NYC als Dienstleistungssystem fungieren.
Das Modell erfasst sowohl das lang- als auch das kurzfristige Verhalten in allen Systemen. Die Übereinstimmung ist bemerkenswert. Sehr wichtig ist hierbei, dass unser Modell es ermöglicht, neue Servicezeiten vorherzusagen. Man braucht nur die Ankunftszeit eines neuen Ereignisses einzugeben (Input), und das Modell gibt aus, wie lange der Dienst dauern wird (Output).
Weitere Informationen im entsprechenden Paper:
Learning Deep Generative Models für Queuing Systems
Cesar Ojeda, Kostadin Cvejoski, Bogdan Georgiev, Christian Bauckhage, Jannis Schuecker, Ramses Sanchez (Proceedings of the AAAI Conference on Artificial Intelligence), 2021, PDF.
