Explainable AI (XAI) has become an important aspect of the development and deployment of Artificial Intelligence systems. As AI continues to play a larger role in our daily lives, it is increasingly important to understand how these systems make decisions and what factors influence their outcomes. This becomes even more urgent with new technologies, such as Quantum Machine Learning, emerging. XAI addresses this need by creating AI systems that can explain their reasoning and provide insights into the decisions they make, or take existing systems and try to explain their behavior in hindsight (post-hoc explanation). This not only helps to build trust in the technology but also allows us to identify potential biases and to make adjustments in order to improve the accuracy and fairness of AI systems. Additionally, the ability to understand and interpret AI decisions is crucial for ensuring that these systems align with ethical and legal standards. By prioritizing XAI, we can ensure that AI develops in a responsible and transparent manner that benefits society as a whole.
Shapley values in XAI
One method from the toolbox of XAI is Shapley values: They were developed by Lloyd Shapley in the 1950s and are a mathematical concept from cooperative game theory. In the context of game theory, Shapley values provide a way to distribute the total value of a cooperative game among its players in a fair and balanced way. The idea is to assign each player a share of the value that is proportional to their contribution to the game.
In recent years, Shapley values have been applied to the field of Machine Learning and Artificial Intelligence, where they can be used to explain the contribution of individual features to a model’s predictions. This is especially relevant for complex models, such as deep neural networks, which can be difficult to interpret. Assume that we have some way to measure the quality of a system’s output, like a score. This could be the prediction accuracy, execution time, energy consumption or any other quantity of interest. Now let us assume that our system can be described as an assembly of N parts (or players), which we simply enumerate from 1 to N. These parts could be neurons in an artificial neural network, features in the input data set, or single models in an ensemble. A function that assigns to each combination of parts a score is called a value function. By computing the Shapley values, we can determine the average contribution of each part to the total value. This gives us a way to evaluate their importance within the whole system. Knowing this makes models more transparent, as we can identify the parts that are responsible for the model’s decision.
Applying Shapley values to Quantum Computing
A somewhat open question has been how Shapley values behave when the value function is not deterministic. In other words, are Shapley values still reliable when the ML system’s properties change over time, can only be estimated, or are subject to any other type of uncertainty? In their recent paper, scientists from the Lamarr Institute’s Explainable AI group joined forces with the Quantum Computing group and researchers from Fraunhofer ITWM to develop a theoretical framework that allows for the evaluation of Shapley values using such uncertain value functions. To this end, they model the value function as a random variable and analyze the effect on the distribution of Shapley values.
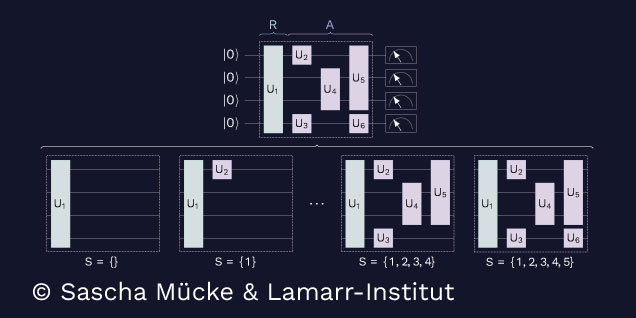
In a follow-up paper, the researchers used their theoretical insights to apply Shapley values to quantum computing [2]. A quantum circuit is the most prominent computational model used to perform quantum computations. It is a series of quantum gates that manipulate the quantum state of a system of quantum bits (or qubits) in order to perform a specific computation. Quantum circuits can be used to perform a wide range of algorithms, including quantum simulations, quantum optimization, and Quantum Machine Learning (QML). Quantum computers can – at least in theory – efficiently solve certain problems that are believed to be intractable for classical computers, such as factoring large numbers and solving certain search problems.
A look inside Quantum Circuits
In a quantum circuit, the qubits are initialized in a known state, and then a series of quantum gates are applied to the qubits to transform their state in a way that corresponds to the desired computation. The final state of the qubits encodes the solution to the problem being solved. Measuring the final state provides a way to extract the solution, but this measurement collapses the quantum state, destroying any remaining quantum coherence. The measurement result is probabilistic, which means that, instead of a single result, a variety of results may be observed with a certain probability every time you measure the quantum state. This can be thought of as rolling a die, where the die itself corresponds to the quantum state, and the measurement result of the roll: Even though the die itself is always the same, the outcome of this “measurement”, that is, the die roll, is non-deterministic. For this reason, every property that we can derive from measuring a quantum state is inherently uncertain.
The individual gates can be thought of as players in a cooperative game, each contributing to the overall behavior of the circuit. By computing the Shapley values for each gate or groups of gates, it becomes possible to determine the contribution of each gate to the final outcome of the circuit, providing a way to explain the behavior of the quantum system.
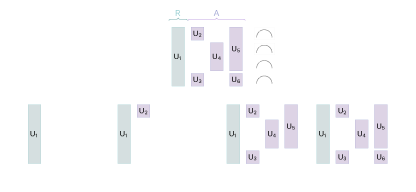
This image shows how a quantum circuit (top) is modified to determine the contribution of each gate: All possible subsets of gates are evaluated separately by removing them from the circuit (bottom) and observing the effect on the value function.
This information can be useful in a variety of contexts, such as debugging and optimization of quantum circuits, as well as in improving the understanding of quantum systems for researchers and practitioners. Furthermore, by using Shapley values to explain the behavior of individual gates, it becomes possible to identify potential issues and make adjustments to improve the accuracy and robustness of quantum circuits. In addition, it allows for the pruning of unnecessary gates in order to reduce the circuit depth, which is a major limiting factor in contemporary quantum computing.
Where XAI and Quantum Computing meet
The value functions used by the researches measure the circuits’ expressibility (that is, the variety of functions they can realize), entanglement capability (how complex the quantum state can become) as well as the classification quality in QML. They use both simulators as well as real quantum computers to compute uncertain Shapley values on a range of different circuits with up to 20 gates. Their results suggest that Shapley values are a promising way to explain the role of specific gates in a quantum circuit, however due to the inherent uncertainty of quantum computing, many measurements are required to compute them faithfully. Classical Shapley values already need a large amount of computational power, and the probabilistic nature of quantum computing exacerbates this problem even further. Therefore, further research is necessary to allow this method to be scaled up.
Overall, the application of Shapley values to quantum circuits is an exciting crossover of XAI and quantum computing research, with the potential to shed some light on how quantum machine learning models work.
More information on this can be found in our publications:
Shapley Values with Uncertain Value Functions
Heese, Raoul et al., 2023, arXiv preprint, pdf
Explaining Quantum Circuits with Shapley Values: Towards Explainable Quantum Machine Learning
Heese, Raoul et al., 2023, arXiv preprint, pdf
