
The meaning of a word is often not apparent solely from its spelling. For instance, “sofa” and “couch” both refer to padded seating for multiple people, but they differ significantly in their spelling. To enable computers to comprehend word meanings, a different representation than letters is needed. This representation can be achieved through embedding vectors. Embedding vectors have a predetermined length and typically contain 100 real numbers, for example. The idea is to construct a unique embedding vector for each word in the language. The embedding vectors for words with similar meanings, such as “sofa” and “couch”, should differ only minimally. The difference in meaning between two words can be assessed, for example, through the Euclidean distance, a geometric measure of the associated embedding vectors. Once the meaning of each word is represented by embedding vectors, the computer can infer the meaning of the entire text.
Highly effective methods have been developed for determining these embedding vectors, such as Word2Vec (see also the article “Automated Keyword Assignment for Short Texts” [German post Link: https://lamarr-institute.org/de/blog/automatisierte-stichwortvergabe-fuer-kurze-texte/]). However, many words have multiple meanings, like “mouse”, which can refer to a computer pointing device or a rodent. Simple word vectors reveal a limitation in that only a single embedding vector is computed for such words, where the meanings overlap.
Consideration of neighboring words in the calculation of context-dependent embedding vectors
Clearly, the neighboring words of “mouse” determine whether it refers to a rodent (The mouse eats cheese) or a computer mouse (Click the mouse button). Alternatively, embedding vectors can be constructed that depend not only on the word itself but also on neighboring words. The relative influence of neighboring words and the word itself can be considered through association modules. The following graphic illustrates such an association module, which is a specific neural network.
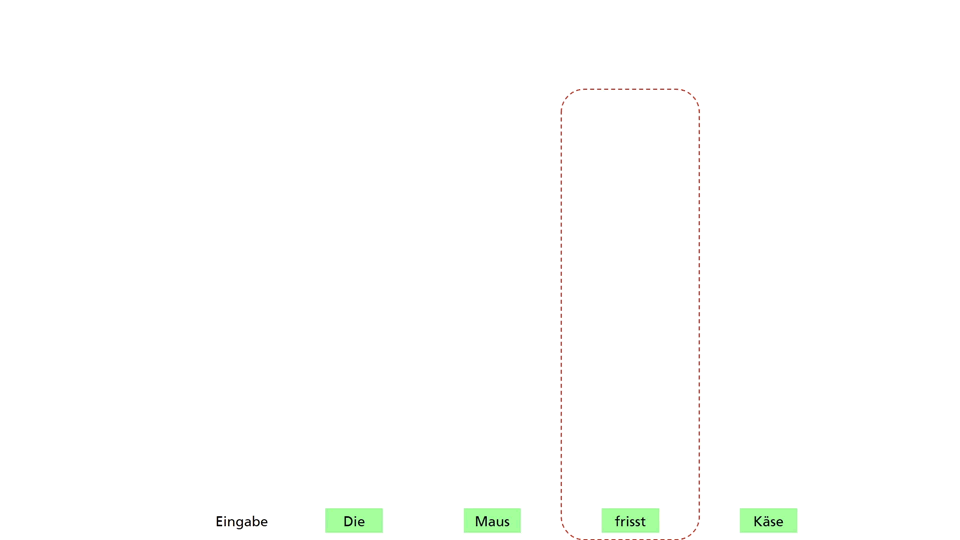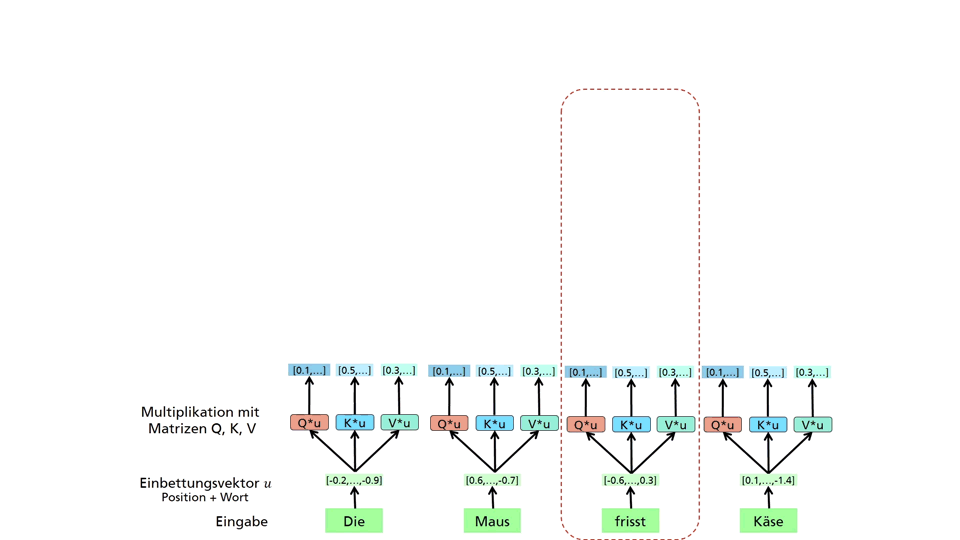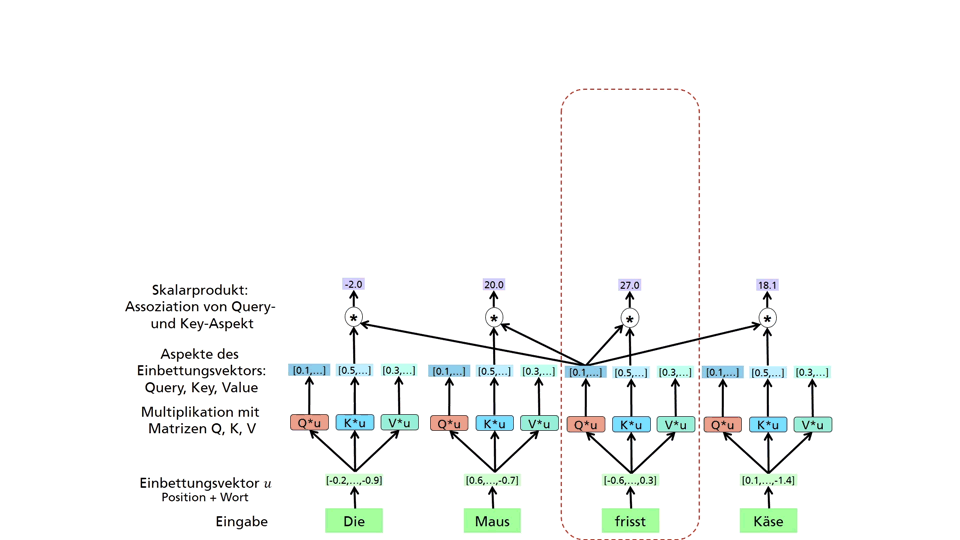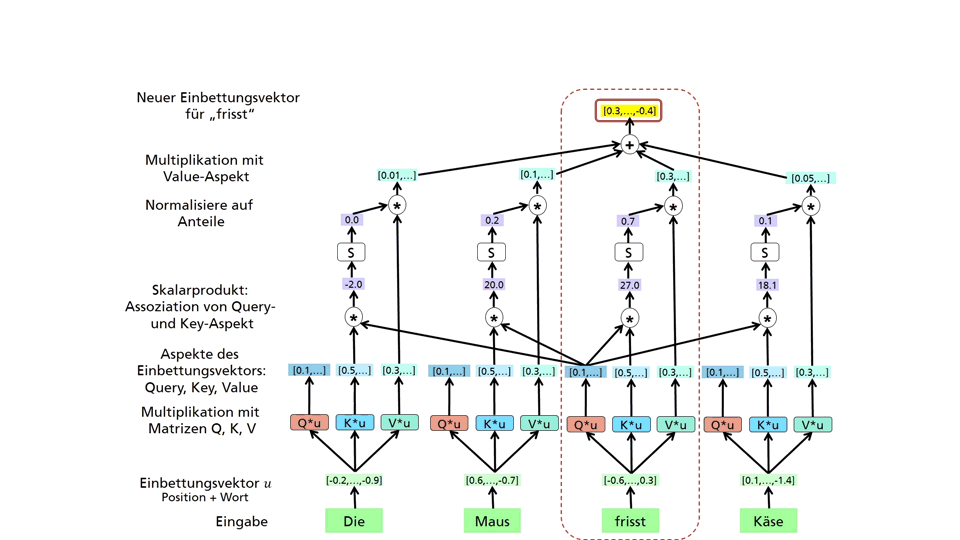
Determination of context-dependent embedding for a word through an association module. The association of the query aspect of the target word “eats” with the key aspects of all words is calculated. The new embedding is formed from the sum of the value aspects of all words weighted by the associations.
Starting from the sentence “The mouse eats cheese,” a new embedding for the word “eats” is to be calculated. For each word in the input, a given embedding vector is used, initially filled with random numbers. To represent the word order, a marking of the word position must be added. Subsequently, the input vectors are multiplied by matrices, whose values are also initially chosen as random numbers.
This generates new vectors (aspects) called Query, Key, and Value. These aspects of the embedding vector focus on different properties of the embedding vector and differ for different association modules. The association of the query vector of “eats” and the key vectors of all words is then calculated through a scalar product. The resulting values are normalized to proportions that add up to 1.0. In the example, “eats” and “mouse” have the strongest association with “eats” regarding the current association module. Finally, the value vectors of all words are added with these weights, resulting in a new embedding vector for the word “eats.” This embedding vector is context-dependent because it has merged the context words, such as “mouse” and “cheese,” and their embeddings with the original embedding.
The following graphic shows the calculation of associations between the word “the” and the words in the sentence “the cat sat on the mat.” The query and respective key vectors are multiplied element-wise and the element-wise product is summed. Strong associations are marked by more intense blue color. As the graphic shows, the word “on” has the strongest association with the word “the” in this sentence.

Calculation of associations between the query vector of “the” and the key vectors of the sentence. The size of the values in the vectors is represented by colors ranging from blue (negative) to orange (positive).
Meaningful embedding vectors require many complementary association modules
However, it has been found that a single association module is not sufficient to determine high-quality embedding vectors. Therefore, a comprehensive model is constructed that uses multiple association modules in parallel in one layer. Each association module has different matrices Q, K, V and can thus focus on different aspects of the embedding vectors. By concatenating the embedding vectors of the layer and a subsequent transformation, new embedding vectors for each word of the input text are then obtained. Several of these layers are stacked on top of each other, ultimately producing the embedding vectors of the last layer.
However, a prediction task is still required to allow training of the unknown parameters of the model. The exact way the probability of replacing the word is predicted can be found in our blog post: “BERT: How Do Vectors Accurately Describe the Meaning of Words?” [German post Link: https://lamarr-institute.org/de/blog/bert/].
