
Many computer programs now use Machine Learning and Artificial Intelligence and are applied in everyday products and processes. They understand spoken language, can interpret texts, recognize objects in photos or support us in personal assistants. Unlike earlier technical systems, their reactions are not individually programmed, but rather they learn from examples.
The blog post “How do machines learn?” has already explained how a computer program can be adapted to data so that it reacts in a certain way. A so-called model is formulated, which receives an input and calculates an output. Depending on the question, the input could be, for example, an image made up of pixels, a sequence of sounds in a voice message, or a text of words and letters. This input is converted into a series of numbers (represented as a vector), which is then processed by the model. The output of a model is again a vector of numbers describing the desired result. This could be, for example, the recognized object in the image, the text of the voice message, or the translation of an input text into another language. In addition, there is also a vector of parameters of the model that specifies in detail how the input is mapped to the output. In this blog post, we want to explain why Deep Learning often achieves higher accuracies than traditional Machine Learning in complex applications.
Neural networks learn from nature’s model
The starting point for Deep Learning was the development of neural networks. Based on the way a human nerve cell works (hence the term “neural networks”), a first model was formulated in the 1950s whose input/output behavior is trainable. Here, a weighted sum of inputs is calculated, where the weights correspond to the connection strength between nerve cells. Interpreting an output value greater than zero as class A and a value less than zero as class B, this model can be used to solve classification problems. The basis for the prediction is a set of training examples, each consisting of an input vector and an associated output. Thereby, the weights within the neural network are adjusted through optimization procedures so that they predict the classes for all training examples as accurately as possible. This model of a simple neural network with one layer is called a perceptron (more in the study on perceptrons).
Here, we consider a simple application example with only two inputs.
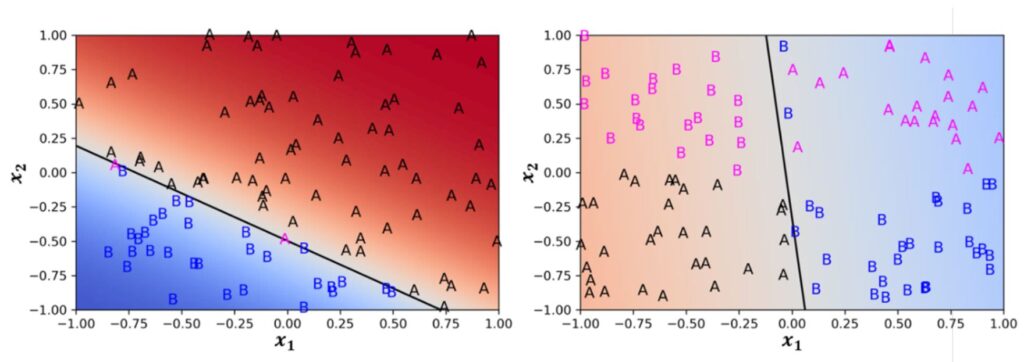
Classification of a neural network with one plane (perceptron)
In the graphic on the left side of the figure, the two input features x1 and x2 are each assigned to a class A or B, respectively. As can be seen, a perceptron always produces a straight dividing line (generally a hyperplane) in the input space. The trained perceptron can separate the two classes very well, so that only two examples (magenta) are assigned incorrectly. On the right side, in the “XOR problem”, the training examples of the two classes are arranged “crosswise”. Here the simple perceptron cannot find a good dividing line.
The two-level perceptron solves the XOR problem
It took more than a decade until a solution was presented for the XOR problem. For this, it is necessary to extend the simple perceptron. First, multiple differently weighted sums are calculated from the inputs, which are then transformed by a nonlinear, increasing function, for example tanh. The results are called hidden units because there are no observational values for these variables in the training data. They serve as input for another perceptron, whose output again predicts the class.
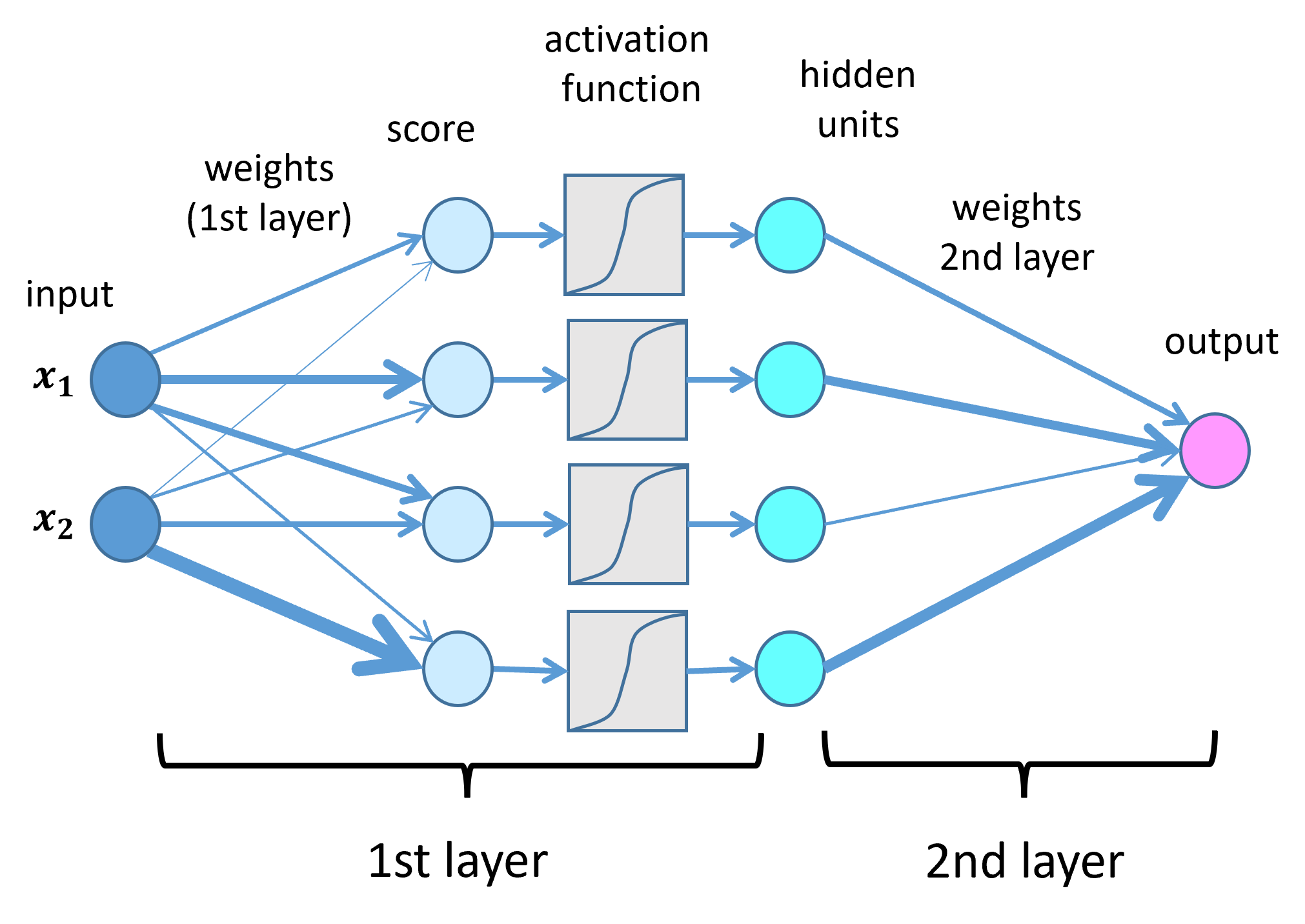
In the figure, the size of the weights is symbolized by the varying thickness of the lines. Crucial is the use of the non–linear function, also called the activation function. This enables the resulting model to predict the curved interfaces for our XOR problem, which a simple perceptron could not represent.
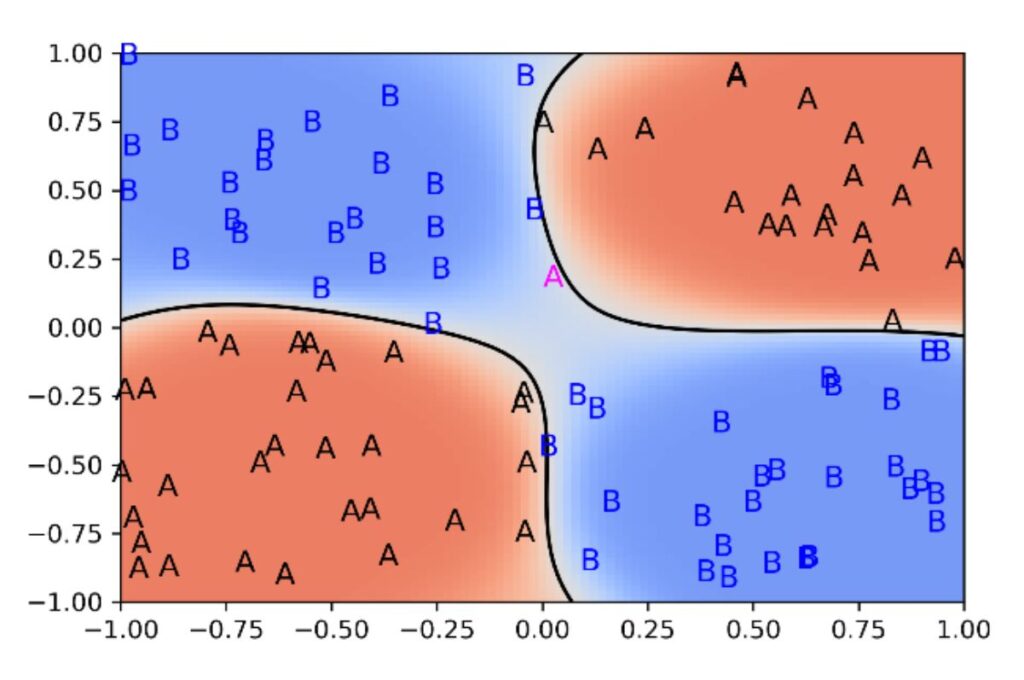
Classification of a deep neural network
As shown in the figure above, the extended model provides an almost perfect solution to the classification problem. It is called a two-layer perceptron. Its weights are determined using the training data by the gradient descent method. Remarkably, the hidden units are a new representation of the inputs, which are constructed by the optimization procedure in such a way that the classification problem is easier to solve. Thus, unlike most classical Machine Learning methods, the two-layer perceptron can internally construct suitable features for problem–solving and make more accurate classifications and predictions.

Example of deep neural networks: recognition of digits
A previously much–discussed task was the recognition of handwritten digits, such as postal codes. The figure above shows example images from the training data. A simple perceptron has an accuracy of 92% on these data. If, however, a two-layer perceptron is used, an accuracy of more than 98% can be achieved, meaning that out of 100-digit images, more than 98 are correctly assigned. This demonstrates that the additional layer can reduce the mapping error to less than a quarter.
Deep Learning enables mapping of complex relationships
It has been demonstrated that two-layer perceptrons can reconstruct arbitrary continuous relationships between inputs and outputs if the number of hidden units is large enough (more on the study). However, the required number of hidden units is often extremely high and there are too few data to reliably determine the parameters. As an alternative, one can extend the model by adding additional layers with further nonlinearities. This is then referred to as a Deep Neural Network, which is investigated in the research area of Deep Learning. Deep Learning is a subarea of Machine Learning that describes “multi–layered learning”, meaning multiple hidden layers in the neural network are used to analyze large datasets. Such a network with three layers is shown in the figure below. It can have multiple outputs, which can be transformed by additional activation functions, for example, into a vector of probabilities. It has been shown that each additional layer of a deep neural network can represent a much larger set of functions than a neural network with fewer layers but with the same number of parameters (more on the study). Thus, a deep neural network promises to efficiently reconstruct very complex relationships between inputs and outputs, such as between the pixels of a photograph and the corresponding image description by a sentence.
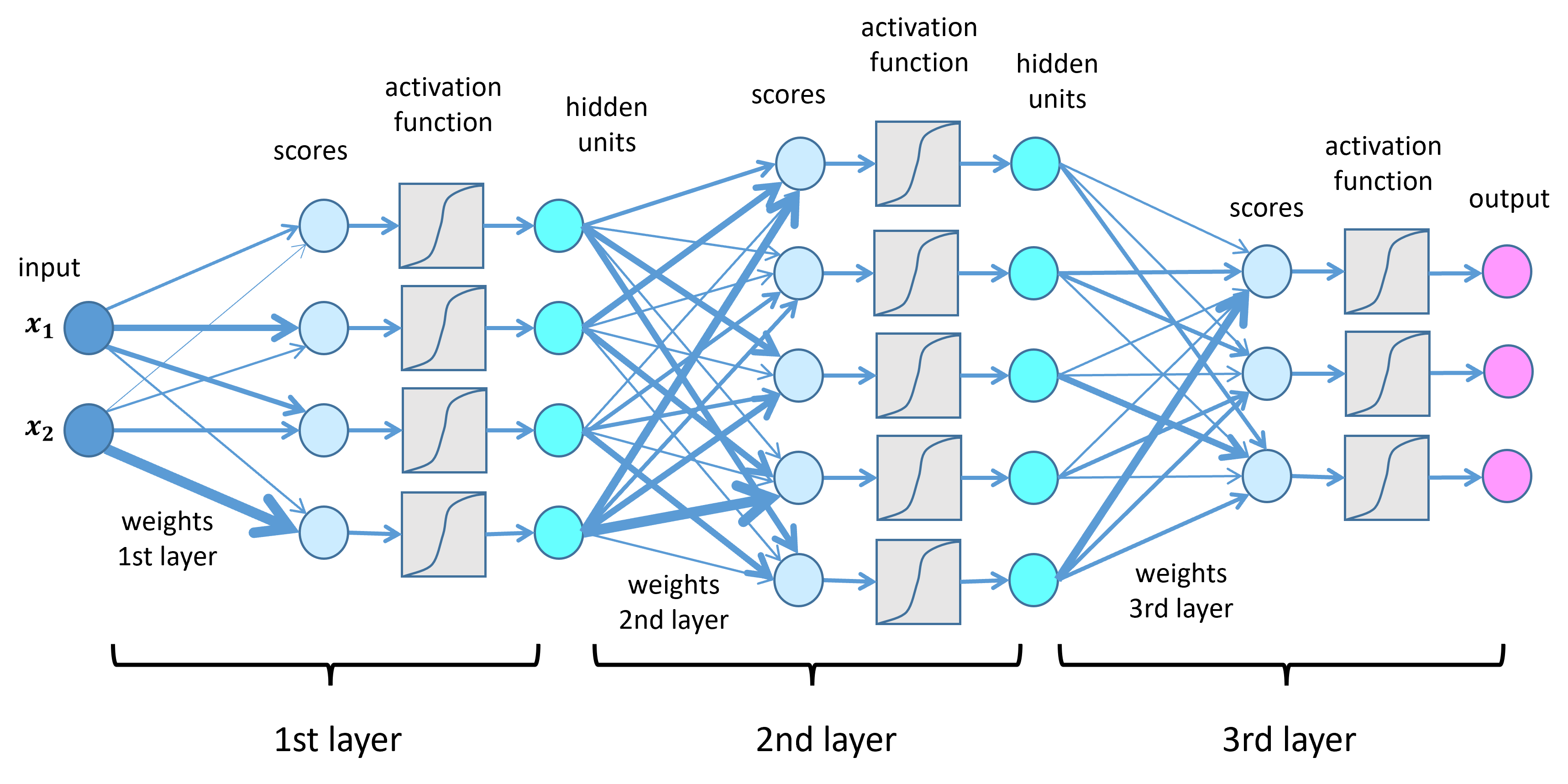
Structure: Deep neural networks
However, optimizing parameters in deep neural networks is extremely challenging because the dependence of outputs on the parameters of the first layers must be reliably reconstructed. This could only be achieved after various techniques were developed. These include regularization methods, such as dropout and normalization of the values of hidden units. These techniques ensure that the network ignores random fluctuations in the data and focuses on systematic relationships. In addition, it has been found that bypass connections, which bridge the individual layers in a controlled manner, allow very deep neural networks to be trained in the first place. The „Künstliche Intelligenz- Was steckt hinter der Technologie der Zukunft?” (Artificial intelligence – What is behind the technology of the future?) provides a detailed presentation of deep neural networks and describes the necessary optimization procedures.
The four pillars of deep neural networks
Deep neural networks for natural language processing, object recognition in images, and speech recognition have a specialized architecture with layers tailored to each application. Today, they often achieve accuracies in recognizing objects and processes that are as good as or higher than those of humans. They typically have dozens to hundreds of layers and form the core of the Deep Learning research area. Overall, their success is based on four pillars:
- The availability of powerful parallel processors to perform the training,
- the collection and annotation of extensive training data,
- the development of powerful regularization and optimization methods, and
- the availability of toolkits to easily define deep neural networks and automatically compute their gradients.
