
Viele Computerprogramme verwenden mittlerweile Maschinelles Lernen und Künstliche Intelligenz und werden in Produkten und Prozessen des Alltags angewendet. Sie verstehen gesprochene Sprache, können Texte interpretieren, erkennen Objekte in Fotos oder unterstützen uns in persönlichen Assistenten. Im Gegensatz zu früheren technischen Systemen werden ihre Reaktionen nicht im Einzelnen programmiert, sondern sie lernen aus Beispielen.
In dem Beitrag „Wie lernen Maschinen?“ wurde bereits dargestellt, wie man ein Computerprogramm an Daten anpassen kann, so dass es in einer bestimmten Weise reagiert. Es wird ein sogenanntes Modell formuliert, welches eine Eingabe erhält und eine Ausgabe berechnet. Je nach Fragestellung kann die Eingabe zum Beispiel ein Bild aus Pixeln, eine Tonfolge in einer Sprachnachricht oder ein Text aus Worten und Buchstaben sein. Diese Eingabe wird umgewandelt in eine Reihe von Zahlen (als ein Vektor repräsentiert), die dann von dem Modell verarbeitet wird. Die Ausgabe eines Modells ist wieder ein Vektor von Zahlen, der das gewünschte Ergebnis beschreibt. Dies kann zum Beispiel das erkannte Objekt im Bild, der Text der Sprachnachricht, oder die Übersetzung eines Eingabetextes in eine andere Sprache sein. Zusätzlich gibt es noch einen Vektor von Parametern des Modells, der im Detail festlegt, wie die Eingabe auf die Ausgabe abgebildet wird. In diesem Beitrag wollen wir erklären, warum Deep Learning in komplexen Anwendungen oft höhere Genauigkeiten als traditionelle maschinelle Lernverfahren erreichen.
Neuronale Netze lernen nach dem Vorbild der Natur
Ausgangspunkt für Deep Learning war die Entwicklung neuronaler Netze. In Anlehnung an die Funktionsweise der Nervenzelle eines Menschen (daher auch der Begriff „Neuronale Netze“) wurde schon in den fünfziger Jahren ein erstes Modell formuliert, dessen Ein-/Ausgabeverhalten trainierbar ist. Dabei wird eine gewichtete Summe der Eingaben berechnet, wobei die Gewichte der Verbindungstärke zwischen Nervenzellen entsprechen. Interpretiert man einen Ausgabewert größer als Null als Klasse A und einen Wert kleiner als Null als Klasse B, so kann man mit Hilfe dieses Modells Klassifikationsprobleme lösen. Grundlage für die Vorhersage ist eine Menge von Trainingsbeispielen, welche jeweils aus einem Eingabevektor und einer zugehörigen Ausgabe bestehen. Dabei werden die Gewichte innerhalb des Neuronalen Netzes durch Optimierungsverfahren so verändert, dass sie die Klassen für alle Trainingsbeispiele möglichst gut prognostizieren. Dieses Modell eines einfachen neuronalen Netzes mit einer Ebene wird Perzeptron genannt (Mehr in der Studie über Perzeptronen).
Hier betrachten wir ein einfaches Anwendungsbeispiel mit nur zwei Eingaben
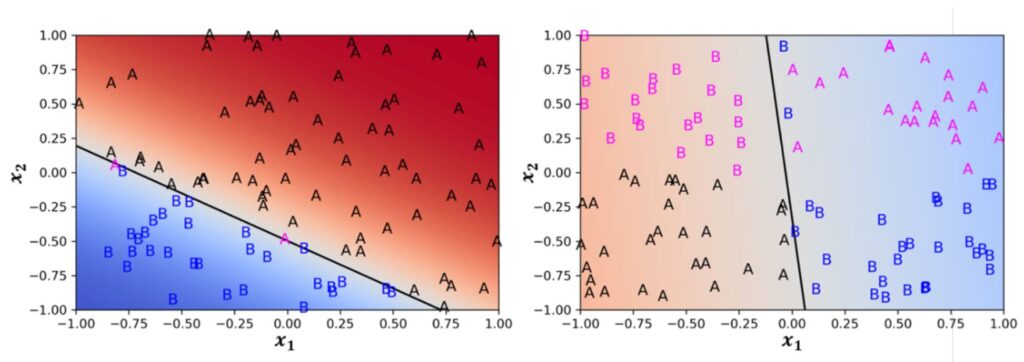
In der Grafik auf der linken Seite der Abbildung ist den zwei Eingabemerkmale [latex]x_{1}[/latex] und [latex]x_{2}[/latex] jeweils eine Klasse A oder B zugeordnet. Wie zu sehen, erzeugt ein Perzeptron immer eine gerade Trennlinie (allgemein eine Hyperebene) im Eingaberaum. Das trainierte Perzeptron kann die beiden Klassen sehr gut trennen, so dass nur zwei Beispiele (magenta) falsch zugeordnet werden. Auf der rechten Seite sind beim „XOR-Problem“ die Trainingsbeispiele der beiden Klassen „über Kreuz“ angeordnet. Hier kann das einfache Perzeptron keine gute Trennlinie finden.
Das Zweiebenen-Perzeptron löst das XOR-Problem
Es dauerte mehr als ein Jahrzehnt, bis für das XOR-Problem eine Lösung präsentiert wurde. Dafür ist es notwendig das einfache Perzeptron zu erweitern. Zunächst werden aus den Eingaben mehrere unterschiedlich gewichtete Summen berechnet, welche anschließend durch eine nichtlineare ansteigende Funktion, zum Beispiel tanh, transformiert werden. Die Ergebnisse heißen verborgene Einheiten (hidden units), weil es für diese Variablen keine Beobachtungswerte in den Trainingsdaten gibt. Sie dienen als Eingabe für ein weiteres Perzeptron, dessen Ausgabe wieder die Klasse prognostiziert.

In der Abbildung ist die Größe der Gewichte durch die unterschiedliche Dicke der Linien symbolisiert. Entscheidend ist die Verwendung der nichtlinearen Funktion, auch Aktivierungsfunktion genannt. Dadurch ist das entstehende Modell in der Lage, die gekrümmten Trennflächen für unser XOR-Problem zu prognostizieren, welche ein einfaches Perzeptron nicht darstellen konnte.
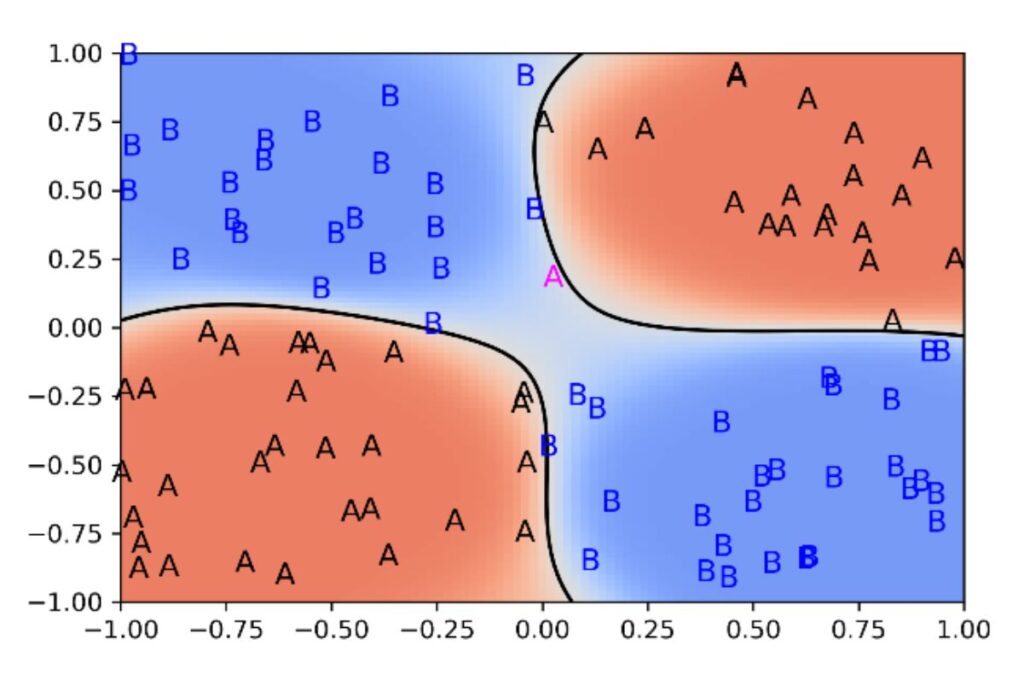
Wie die vorstehende Abbildung zeigt, liefert das erweiterte Modell eine nahezu perfekte Lösung des Klassifikationsproblems. Es wird Zweiebenen-Perzeptron genannt. Seine Gewichte werden mit Hilfe der Trainingsdaten durch das Gradientenabstiegsverfahren bestimmt. Bemerkenswert ist, dass die verborgenen Einheiten eine neue Repräsentation der Eingaben sind, die durch das Optimierungsverfahren so konstruiert werden, dass das Klassifikationsproblem leichter lösbar ist. Im Gegensatz zu den meisten klassischen Verfahren des Maschinellen Lernens ist das Zweiebenen-Perzeptron also in der Lage, intern geeignete Merkmale für die Problemlösung zu konstruieren und genauere Klassifikationen und Vorhersagen zu treffen.

Eine früher viel diskutierte Aufgabe war die Erkennung von geschriebenen Ziffern, beispielsweise Postleitzahlen. Die vorstehende Abbildung zeigt Beispielbilder aus den Trainingsdaten. Ein einfaches Perzeptron hat auf diesen Daten eine Genauigkeit von 92%. Verwendet man hingegen ein Zweiebenen-Perzeptron, so kann man eine Genauigkeit von mehr als 98% erreichen, das heißt von 100 Zifferbildern werden mehr als 98 korrekt zugeordnet. Dies zeigt, dass die zusätzliche Ebene den Zuordnungsfehler auf weniger als ein Viertel reduzieren kann.
Deep Learning ermöglicht das Abbilden komplexer Zusammenhänge
Es konnte gezeigt werden, dass Zweiebenen-Perzeptronen beliebige stetige Zusammenhänge zwischen den Ein- und Ausgaben rekonstruieren können, wenn nur die Anzahl der verborgenen Einheiten groß genug ist (Mehr zu der Studie). Allerdings ist die erforderliche Anzahl der verborgenen Einheiten oft extrem hoch und es gibt zu wenige Daten, um die Parameter zuverlässig zu bestimmen. Als Alternative kann man das Modell durch zusätzliche Ebenen mit weiteren Nichtlinearitäten erweitern. Man spricht dann von einem Tiefen Neuronalen Netz, welches im Forschungsbereich Deep Learning untersucht wird. Dabei ist Deep Learning ein Teilbereich des Maschinellen Lernens und beschreibt „mehrschichtiges Lernen“, das heißt es werden mehrere versteckte Ebenen im neuronalen Netz genutzt, um große Datensätze zu analysieren. Ein derartiges Netz mit drei Ebenen ist in der folgenden Abbildung gezeigt. Es kann mehrere Ausgaben besitzen, welche durch zusätzliche Aktivierungsfunktionen transformiert werden können, zum Beispiel in einen Vektor von Wahrscheinlichkeiten. Es konnte gezeigt werden, dass jede zusätzliche Schicht eines tiefen neuronalen Netzes eine wesentlich größere Menge von Funktionen darstellen kann als ein neuronales Netz mit weniger Schichten, aber mit der gleichen Anzahl von Parametern (Mehr zu der Studie). Damit verspricht ein tiefes neuronales Netz die effiziente Rekonstruktion sehr komplexer Zusammenhänge zwischen Ein- und Ausgaben, beispielsweise zwischen den Pixeln eines Fotos und der zugehörigen Bildbeschreibung durch einen Satz.

Allerdings ist die Optimierung der Parameter in tiefen neuronalen Netzen äußerst schwierig, weil die Abhängigkeit der Ausgaben von den Parametern der ersten Schichten zuverlässig rekonstruiert werden muss. Dies konnte erst gelingen, nachdem verschiedene Techniken entwickelt wurden. Dazu gehören Regularisierungsverfahren, wie Dropout und die Normalisierung der Werte der verborgenen Einheiten. Diese sorgen dafür, dass das Netzwerk zufällige Fluktuationen in den Daten ignoriert und sich auf systematische Zusammenhänge konzentriert. Zudem hat es sich gezeigt, dass Bypass-Verbindungen, welche die einzelnen Ebenen gesteuert überbrücken, überhaupt erst das Training sehr tiefer Neuronaler Netze erlauben. Die Monografie „Künstliche Intelligenz — Was steckt hinter der Technologie der Zukunft?“ gibt eine detaillierte Darstellung tiefer neuronaler Netze und beschreibt die erforderlichen Optimierungsverfahren.
Die vier Säulen tiefer neuronaler Netze
Tiefe neuronale Netze zur Verarbeitung natürlicher Sprache, zur Erkennung von Objekten in Bildern, und zur Spracherkennung haben eine spezialisierte Architektur mit Schichten, die auf die jeweiligen Anwendungen zugeschnitten sind. Sie erreichen heute oft Genauigkeiten bei der Erkennung von Objekten und Abläufen, welche genauso gut oder höher sind als die von Menschen. Sie haben meist Dutzende bis Hunderte von Schichten und bilden den Kern des Forschungsbereiches Deep Learning. Insgesamt beruht ihr Erfolg auf vier Säulen:
- der Verfügbarkeit von leistungsfähigen parallelen Prozessoren zur Durchführung des Trainings,
- der Sammlung und Annotation umfangreicher Trainingsdaten,
- der Entwicklung leistungsfähiger Regularisierungs- und Optimierungsverfahren und
- der Verfügbarkeit von Toolkits, mit denen tiefe neuronale Netze auf einfache Weise definiert und deren Gradienten automatisch ausgerechnet werden.
