Tagtäglich interagieren wir auf der Arbeit, beim Sport oder auch im Internet in Form von sozialen Netzwerken mit anderen Leuten innerhalb sozialer Strukturen. Graphen sind ein grundlegendes Konzept der Informatik, die in der Lage sind, diese komplexen Systeme und Beziehungen zu modellieren.
Im Bereich der KI finden Graph Neural Networks (GNNs) Anwendung. GNNs sind künstliche neuronale Netze, die auf Daten mit Graphstruktur arbeiten und die Fähigkeit besitzen, eben jene Beziehungen zu analysieren. Um Aufgaben wie die Knotenklassifikation (z. B. zur Erkennung von Fake-Accounts in sozialen Netzwerken), die Vorhersage von Beziehungen (z. B. von biologischen Interaktionen zwischen Proteinen) oder die Klassifikation von ganzen Graphen (z. B. zur Bestimmung der Toxizität eines Moleküls auf der Grundlage seiner Struktur) zu ermöglichen, nutzen GNNs das Message Passing Modell, bei dem Informationen von benachbarten Knoten kombiniert werden. Doch sehen wir uns zunächst an, was Graphen eigentlich sind.
Was sind Graphen?
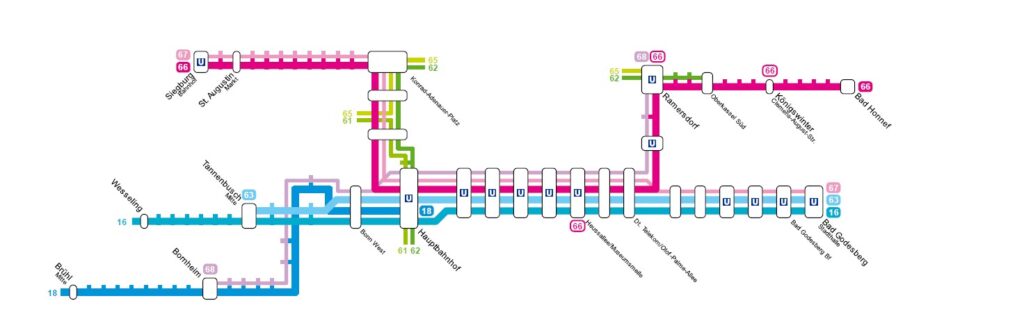
Ein einzelner Graph ist die mathematische Abstraktion einer Menge von Objekten (Knoten) und der Verbindungen zwischen diesen Objekten (Kanten). Die Kanten können entweder gerichtet oder ungerichtet sein. In gerichteten Graphen können Kanten nur in eine Richtung durchlaufen werden, während in ungerichteten Graphen die Richtung keine Rolle spielt. Diese Struktur eignet sich zur Modellierung von Beziehungen zwischen verschiedenen Objekten und kann dabei helfen, komplexe Zusammenhänge zu visualisieren und zu analysieren. Ein anschauliches Beispiel eines Graphen ist ein U-Bahn-Netz, in dem jede Station durch einen Knoten repräsentiert wird und jede Kante eine direkte Verbindung zwischen zwei Stationen darstellt.
Was unterscheidet GNNs von herkömmlichen künstlichen neuronalen Netzen?
Herkömmliche neuronale Netze sind auf die Verarbeitung von Vektoren oder Matrizen, also Daten, die eine regelmäßige Struktur aufweisen, spezialisiert und liefern in vielen Anwendungsfällen hervorragende Ergebnisse. Schwierigkeiten haben sie jedoch bei der Verarbeitung von Beziehungen zwischen Datenpunkten sowie von Daten ohne feste Struktur.
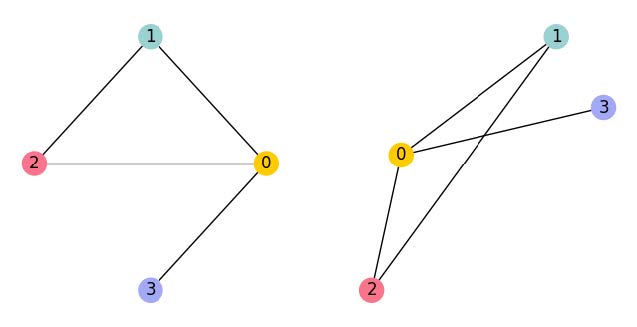
Diese Daten und ihre Beziehungen werden jedoch durch Graphen modelliert. Wie in Abbildung 2 verdeutlicht, sind die Knoten eines Graphen nicht an eine feste Position im Raum gebunden, sodass die kürzeste Distanz zwischen zwei Knoten durch den kürzesten Weg über die Kanten und nicht durch die Entfernung im Raum definiert ist. Die Beziehungen zwischen Datenpunkten werden durch die Kanten verkörpert.
Um mit diesen Beziehungen und Daten ohne feste Struktur arbeiten zu können, wurden GNNs entwickelt. Diese nutzen den Aufbau des Graphen, um lokale Informationen über die Nachbarschaft der Knoten zu aggregieren und zu verarbeiten.
Wie GNNs funktionieren – Das Message Passing Modell
Um die Funktionsweise von GNNs zu verstehen, ist es notwendig, sich zunächst mit dem Message Passing Modell vertraut zu machen. Dessen Grundidee besteht darin, dass Knoten untereinander Nachrichten austauschen, in denen sie eigene Merkmale an ihre Nachbarn weitergeben. Diese Informationen werden dann kombiniert, um aktualisierte Repräsentationen der Knoten zu erzeugen. Dabei wird davon ausgegangen, dass miteinander verbundene Knoten ähnliche Eigenschaften aufweisen.
Konkret bedeutet das, dass jeder Knoten einen Vektor von Merkmalen erhält, der seine aktuelle Repräsentation darstellt. Dieser Vektor wird dann mit den Merkmalsvektoren seiner Nachbarn kombiniert, um eine neue Repräsentation zu generieren, die wiederum im nächsten Schritt an seine Nachbarn weitergegeben wird. Nach $k$ Wiederholungen enthält die Repräsentation eines Knotens die Informationen der benachbarten Knoten, die $k$ Schritte entfernt sind.
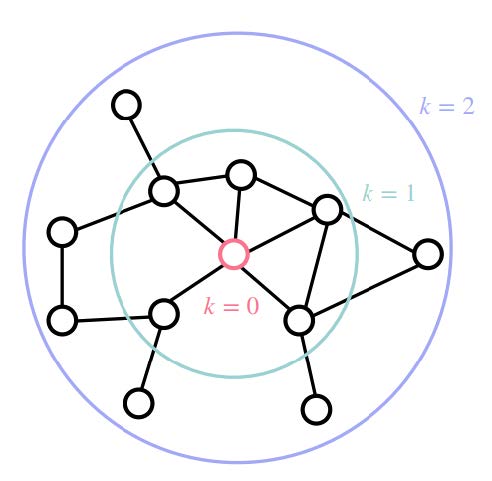
Diese iterative Methode der Nachrichtenweitergabe ermöglicht es den GNNs, eine Repräsentation des Graphen zu generieren, indem sie die Informationen von jedem Knoten und dessen Nachbarn kombinieren. Die endgültige Repräsentation des Graphen kann dann zur Klassifikation, Vorhersage von Beziehungen oder anderen Aufgaben genutzt werden.
Hierzu kommen verschiedene Arten von GNNs zum Einsatz, die sich in der Methode des Message Passings unterscheiden. Drei beliebte Modelle sind Graph Convolutional Networks (GCN), Graph Attention Networks (GATs) und GraphSAGE. Im Folgenden wird beispielhaft auf Graph Convolutional Networks eingegangen. Einen detaillierteren Einblick in die Anwendungen von GATs finden Sie im Beitrag Automatische Klassifikation eines Publikationsnetzwerks mithilfe eines Graph Attention Networks.
Graph Convolutional Networks
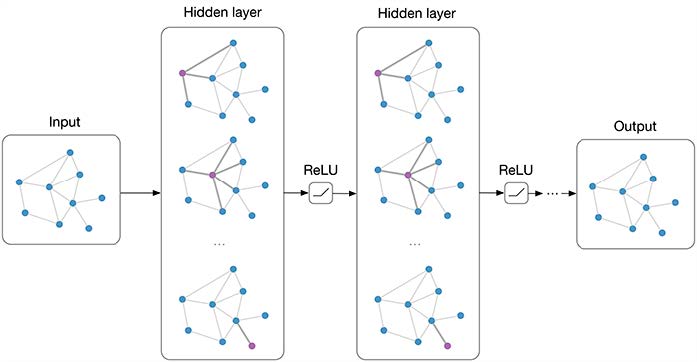
Graph Convolutional Networks sind eine beliebte Methode zur Klassifizierung von Knoten in einem Graphen. Sie bestehen ähnlich wie klassische Convolutional Neural Networks aus $k$ Schichten, in denen eine Repräsentation der Knoten in der jeweiligen verdeckten Schicht gelernt wird. Um diese Repräsentationen erlernen zu können, wird zunächst die Adjazenzmatrix des Graphen benötigt.
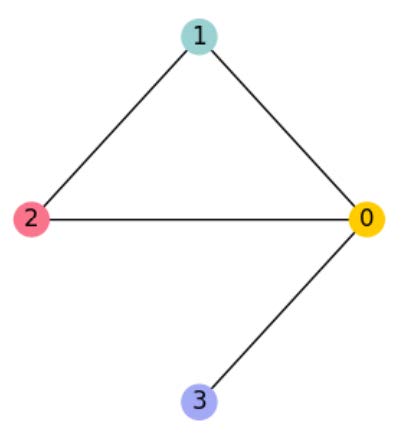
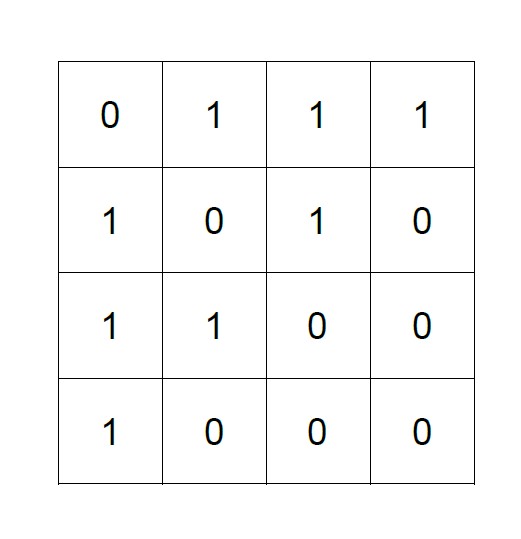
Das Erlernen der Repräsentationen erfolgt durch das Multiplizieren der Adjazenzmatrix $A$ mit der Node-Feature Matrix $X$, in der die Merkmalsvektoren aller Knoten zusammengetragen sind, und einer Gewichtsmatrix $W$. Jede verdeckte Schicht besitzt je eine zugehörige Matrix $W^{(k)}$. In der Praxis haben sich zwei Schichten bewährt, da sie eine ausreichend komplexe Darstellung des Graphen ermöglichen, ohne zu einer Überanpassung des Modells an die Trainingsdaten zu führen.
Um nicht-lineare Beziehungen zwischen Knoten erfassen zu können, wird eine nicht-lineare Aktivierungsfunktion $\sigma$, wie z.B. die $ReLU (f(x) = \max(0, x))$, hinzugefügt, sodass sich die Berechnung der Repräsentationen in der nächsten Schicht wie folgt ergibt:
$H^{(k+1)} = \sigma(AH^{(k)}W^{(k)})$
Durch die Multiplikation der Adjazenzmatrix und der Node-Feature Matrix werden die Informationen der benachbarten Knoten aufsummiert und schließlich durch Multiplizieren mit einer Gewichtsmatrix gewichtet. Die Gewichtsmatrix enthält die Gewichte, die das Modell lernt, um die Beziehungen zwischen den Knoten im Graphen zu modellieren. Diese Gewichte werden dann während des Lernprozesses mittels des Gradientenabstiegsverfahrens angepasst, um eine bestmögliche Repräsentation zu generieren.
Fazit
Graph Neural Networks sind ein leistungsstarkes Instrument zur Analyse und Vorhersage von Beziehungen zwischen Objekten. Sie unterscheiden sich von herkömmlichen künstlichen neuronalen Netzen dadurch, dass sie Beziehungen zwischen Datenpunkten berücksichtigen, indem sie Daten in Form von Graphen verarbeiten können. Dabei nutzen sie die Message Passing Methode, um durch Informationstransfer mit Nachbarn die Knotenrepräsentationen zu lernen. Diese können anschließend zur Knotenklassifikation, Vorhersage von Beziehungen oder zur Graphenklassifikation verwendet werden. Infolgedessen finden GNNs in vielen Bereichen Anwendung und werden voraussichtlich auch in Zukunft eine wichtige Rolle spielen.
