
Word embeddings play a central role in the machine analysis of texts. A central problem in the computer-driven analysis of text data is how to make words, which consist of pure strings, readable for systems that mostly operate based on numerical vectors. In addition, other research areas, including those at the ML2R competence center (now the Lamarr Institute), deal with the important question of the interpretability of word representations. But before we introduce our developed approach, we will explain how text data is made readable in the system.
A first approach to solving this challenge is provided by so-called word embeddings, i.e., vector representations for words. Word embeddings assign a vector of a fixed size to each word in a given vocabulary after these vectors have been calculated on training data. The usefulness of these representations depends on the algorithm used, the training data, the vocabulary, and the size of the vectors. Once word embeddings have been well trained, they exhibit the interesting property that semantic relationships between words are transferred to geometric relationships between the respective vectors. A famous example of this can be shown with word2vec word embeddings:

Semantically, “king” is to “man” as “queen” is to “woman”. This similarity is also reflected in the learned word embedding vector space.
Subtracting the vector for ‘man’ from the original vector ‘king’ and adding the vector for ‘woman’ instead yields a vector that is very similar to the vector ‘queen’. These relationships between vectors now enable the analysis of texts with the help of self-learning systems and the classification of words and entire paragraphs.
Advantages and disadvantages of word embedding models
The most well-known word embedding models (such as GloVe and word2vec) are based on matrix factorization. For a given vocabulary of size n, an input matrix of size ntimesn is created from training data, which holds relationships between words in the entire text corpus. The input matrix counts how often a word occurs in relation to other words (for example, in the same sentence or in a specified context), which is also called co-occurrence. This matrix is then factorized into matrices of smaller dimensionality, compressing the information from the input matrix into smaller dimensions. This requires relationships between words to be included in the smaller representations. Thus, the meaning of a word is defined by the words that often occur in its vicinity – consistent with the well-known quote from the linguist John Rupert Firth: “You shall know a word by the company it keeps” (1957).
Although word embeddings are very useful for many tasks, they also have significant disadvantages: to represent all the information of the training data, the vectors must have a certain size. Common models generate vectors of lengths between 50 and 300 numbers. This means that a word is represented by up to 300 numbers. It is not clear whether individual numbers represent different properties of the word or whether only the geometric relationships of the complete vectors determine the representation.
Due to the lack of transparency, it is hardly possible to examine a model that classifies text based on these vectors in detail. If a word is misclassified, the error may be traced back to individual dimensions of the input data (word vectors). However, the individual dimensions are not readily interpretable, making the analysis difficult to continue.
Interpretable DEDICOM factorization
Therefore, in a recent study by our researchers, an approach to improved interpretability has been developed: word vectors through DEDICOM matrix factorization. DEDICOM stands for Decomposition into Directed Components and has already been used in research to study social networks, email traffic, and usage behavior in computer games. However, applying it to word vectors describes a new approach.

The DEDICOM algorithm factorizes a square input matrix 𝑆 into a weight matrix 𝐴 and a connection matrix 𝑅.
But what makes this approach special? DEDICOM represents a special type of factorization of a square matrix: an input matrix S of size ntimesn is divided into a weight matrix A of size ntimesk and a connection matrix R of size ktimesk, so that S=ARAT. The input matrix S, as in other word embedding algorithms, forms an adapted co-occurrence matrix of the training corpus with vocabulary size n.
The factor matrix A then outputs k-dimensional word vectors, where k is chosen significantly smaller than with other algorithms. If the calculated word vectors are sorted in descending order according to their individual components, groups of words that belong together thematically are obtained. Thus, the main topics of the original text have been extracted, and they can be identified by the associated words. Additional constraints on the factorization algorithm allow each word vector to represent a probability distribution over the topics. That means, the third entry of a word vector indicates the probability of the word being assigned to the third topic.
Matrix R indicates which topics occur together particularly often. For example, if we choose 10 for k, matrix R then indicates the relationship between the 10 dimensions (topics): a large value in row 3 and column 6 means that words with significant weight in the 3rd and 6th entries of their vectors often occur together in the text. This allows the individual dimensions to be understood as thematic components of the text corpus.
ARAT represents the reconstructed S matrix. The more similar ARAT is to S, the more accurately the information from the input matrix has been extracted.
DEDICOM hands-on example
To illustrate the advantages of DEDICOM factorization in practice, we will now take a closer look at a selected example from our study. The table shows the topics extracted with DEDICOM from an artificial text corpus consisting of the English Wikipedia articles “Johnny Depp”, “Bee”, and “Soccer”.
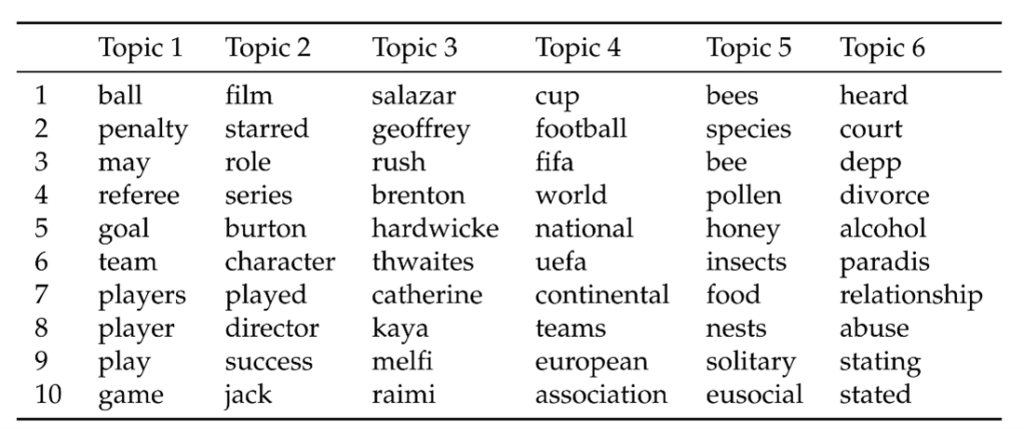
Descending sorted word vectors per dimension. By examining the listed vectors, the individual dimensions can be interpreted as topics.
It can be quickly seen that topics 1 and 4 can clearly be attributed to the “Soccer” article. While topic 1 focuses on the gameplay mechanics, topic 4 covers the professional or structural aspect of soccer. Taking a closer look at topic 6, it becomes clear that the difficult relationship between actor Johnny Depp and his ex-wife Amber Heard is addressed very specifically.
Now, let’s continue the analysis further: in Table 2, we analyze the learned vector space by determining the four most similar words for the most important word of each topic. Similarity is defined here as the cosine similarity between two-word vectors. It can be seen that our DEDICOM algorithm, similar to word2vec and GloVe, encodes the semantic similarity between words like “film” and “starred” in topic 2 in the learned vector space as well.
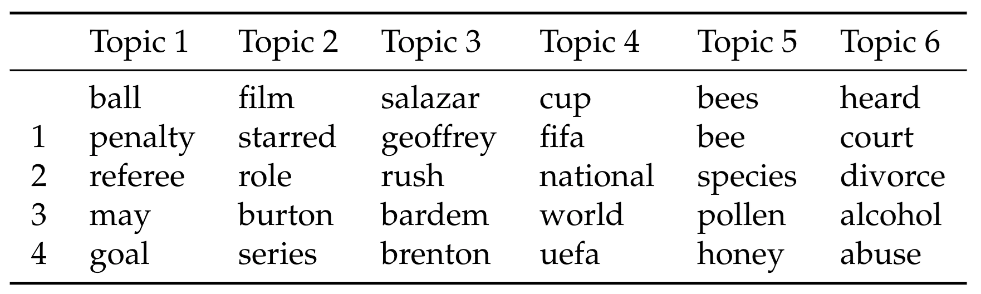
Descending sorted word vectors per dimension. By examining the listed vectors, the individual dimensions can be interpreted as topics.
Furthermore, DEDICOM allows for the simultaneous extraction of relevant topics and the generation of interpretable word vectors from the given text corpus: each entry in the vector indicates the probability of the associated word being assigned to the corresponding topic of the entry. Machine Learning models built on our interpretable word vectors are thus easier to analyze. If errors in classification can be traced back to individual dimensions of the input data, a thematic interpretation of the classification is possible.
In summary: The DEDICOM algorithm is suitable for the simultaneous extraction of topics and the representation of words through interpretable word vectors. The latter can also be used for further machine learning models to promote their explainability.
For more information on the algorithm, detailed experiments, and comparisons with other methods, please refer to the corresponding publication:
Interpretable Topic Extraction and Word Embedding Learning using row-stochastic DEDICOM
L. Hillebrand, D. Biesner, C. Bauckhage, R. Sifa. CD-MAKE, 2020, Link.

