Every day, whether at work, during sports, or online in social networks, we interact with other people within social structures. Graphs are a fundamental concept in computer science that can model these complex systems and relationships.
In the field of AI, Graph Neural Networks (GNNs) are utilized. GNNs are artificial neural networks designed to work with graph-structured data and have the capability to analyze such relationships. They are employed for tasks such as node classification (e.g., detecting fake accounts in social networks), relationship prediction (e.g., predicting biological interactions between proteins), or graph classification (e.g., determining a molecule’s toxicity based on its structure). GNNs achieve this using the message-passing model, which combines information from neighboring nodes. But first, let us examine what graphs are.
What are graphs?
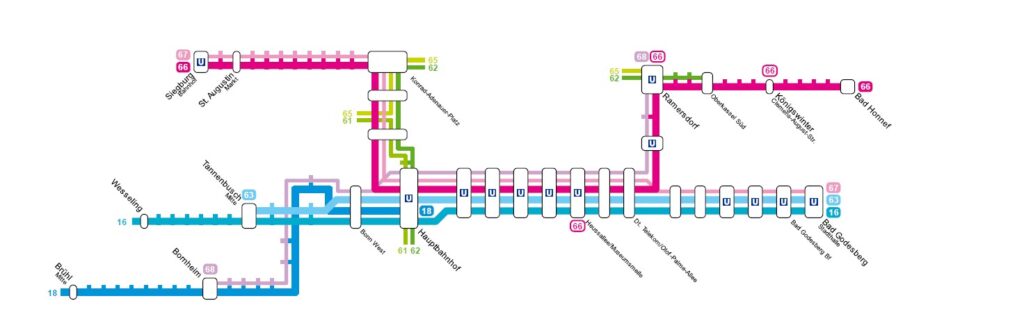
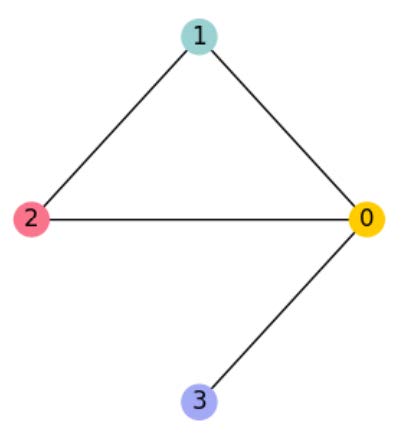
A graph is a mathematical abstraction representing a set of objects (nodes) and the connections between them (edges). The edges can be either directed or undirected. In directed graphs, edges have a specific direction, while in undirected graphs, direction does not matter. This structure is well-suited for modeling relationships between different objects and can help visualize and analyze complex connections. A relatable example of a graph is a subway network, where each station is represented by a node, and each edge represents a direct connection between two stations.
How are GNNs different from traditional artificial neural networks?
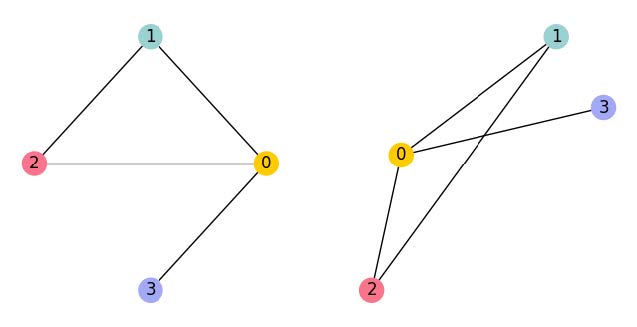
Traditional neural networks are specialized for processing vectors or matrices—data with a regular structure—and perform excellently in many applications. However, they struggle when handling relationships between data points or data without a fixed structure.
These relationships and data are modeled by graphs. As illustrated in Figure 2, the nodes of a graph are not bound to a fixed position in space. The shortest distance between two nodes is determined by the shortest path along the edges rather than the spatial distance. The relationships between data points are embodied by the edges.
To work with these relationships and unstructured data, GNNs were developed. They leverage the graph’s structure to aggregate and process local information from a node’s neighborhood.
How GNNs work – the message passing model
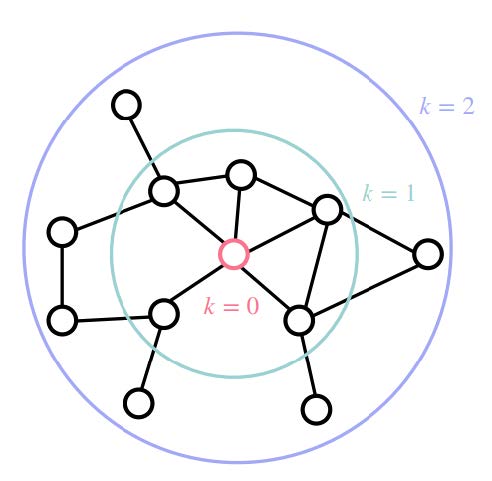
To understand how GNNs function, it is essential to familiarize oneself with the message-passing model. The core idea of this model is that nodes exchange messages with each other, sharing their features with their neighbors. These messages are then combined to generate updated representations of the nodes. The assumption is that connected nodes tend to have similar properties.
Specifically, each node is assigned a vector of features representing its current state. This vector is combined with the feature vectors of its neighbors to generate a new representation, which is then passed on to its neighbors in the next step. After $k$ iterations, a node’s representation contains information from all its neighbors up to $k$ steps away.
This iterative message-passing method allows GNNs to generate a representation of the graph by combining information from each node and its neighbors. The final representation of the graph can then be used for classification, relationship prediction, or other tasks.
Various types of GNNs are employed, differing in how they perform message passing. Three popular models are Graph Convolutional Networks (GCNs), Graph Attention Networks (GATs), and GraphSAGE. Below, we focus on Graph Convolutional Networks as an example. For a more detailed look at GAT applications, refer to the blog post Automatic Classification of a Publication Network Using a Graph Attention Network.
Graph Convolutional Networks
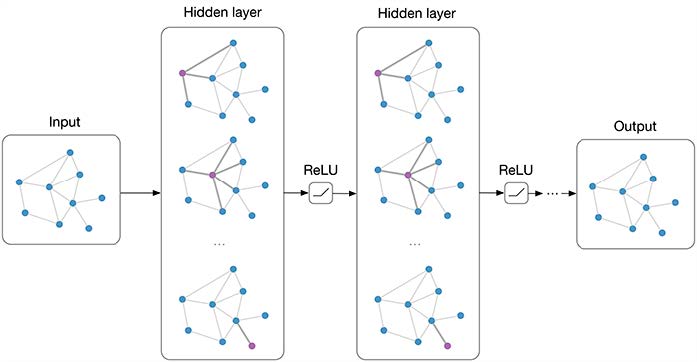
Graph Convolutional Networks are a popular method for node classification within a graph. Similar to classical Convolutional Neural Networks (CNNs), they consist of $k$ layers where the representation of nodes in each hidden layer is learned. To learn these representations, the adjacency matrix of the graph is required.
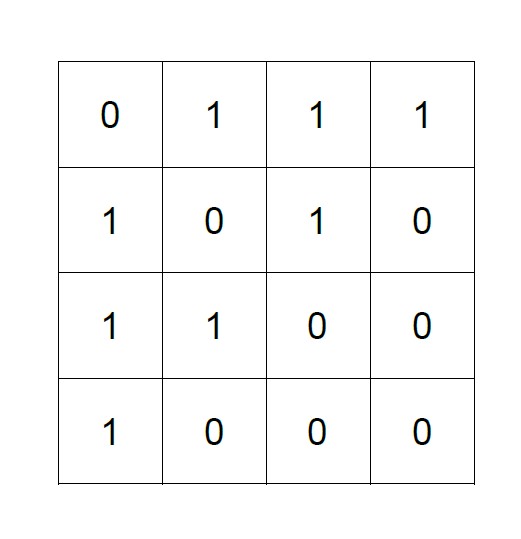
The learning process involves multiplying the adjacency matrix $A$ with the node feature matrix $X$, which contains the feature vectors of all nodes, and a weight matrix $W$. Each hidden layer has its associated weight matrix $W^{(k)}$. In practice, two layers are often sufficient, providing a complex enough representation of the graph without leading to overfitting to the training data.
To capture non-linear relationships between nodes, a non-linear activation function $\sigma$, such as $ReLU (f(x) = \max(0, x))$, is applied. The representation of nodes in the next layer is calculated as follows:
$H^{(k+1)} = \sigma(AH^{(k)}W^{(k)})$
By multiplying the adjacency matrix and the node feature matrix, information from neighboring nodes is aggregated. This is then weighted by multiplying with the weight matrix. The weight matrix contains parameters learned by the model to represent relationships between nodes. These weights are adjusted during training using gradient descent to generate the best possible representation.
Fazit
Graph Neural Networks are a powerful tool for analyzing and predicting relationships between objects. They differ from traditional artificial neural networks by accounting for relationships between data points, processing data in the form of graphs. Using the message-passing method, GNNs learn node representations through the transfer of information with neighbors. These representations can then be used for node classification, relationship prediction, or graph classification. Consequently, GNNs find applications in various fields and are expected to play a significant role in the future.
