The problem – too many possibilities
Many people in research and development departments around the world face the same task: developing something new. How can a battery be designed to make an electric car run longer? How can a wind turbine rotor be modified to produce less noise? What would a new detergent look like that cleans effectively but uses fewer resources? The possible answers to these questions are often very diverse. There are (too) many possibilities for how existing technology could be changed or improved.
Unfortunately, not all ideas can be tested, as each experiment, whether a simulation or a real one in the lab, costs time, money, and resources. For researchers, it would be a dream to be able to conduct all experiments, but they too work with limited resources.
Design of Experiments – a solution
This is where Design of Experiments (DoE) comes into play. The basic idea is simple: Can a good experimental design (Design of Experiments) help reduce the number of experiments needed? How can it be checked if a certain factor has any influence on the target variable? And how can the size of the factor’s influence be estimated? With a good DoE, only the statistically necessary experiments should be conducted, not all possible ones.
It is important to relate this to the Curse of Dimensionality. One can imagine a coffee machine, whose (unknown) switches (factors) you want to understand: Each additional factor (e.g., grind size, water temperature, brewing time, etc.) increases the dimension and simultaneously the number of experiments that can and must be conducted to, for example, find the best-tasting espresso the machine can produce. The exponential growth of points needed to fill the space (here: the experiments required to draw statistically valid conclusions) is referred to as the Curse of Dimensionality.
A good DoE now serves to conduct only the necessary experiments and reduce the influence of the Curse of Dimensionality. For this, assumptions must first be made: Is the influence of the factor more likely to be monotonic (the longer it brews, the stronger the coffee), or, for example, quadratic (very coarse beans produce poor coffee, very finely ground beans do too-there is an optimum in between)? Based on this, an initial DoE can be set up to test these assumptions: For the brewing time, at least two variations (low/high) are needed, and for the grind size three (low/medium/high). This results in six necessary experiments: the variation of brewing time across all three grind sizes. If one additionally assumes that there is no interaction between the two variables, even four would suffice–two at a fixed grind size to determine the influence of brewing time, and three where the grind size is varied at a fixed brewing time.
At first glance, this approach is very plausible–but it becomes more complicated when the formulation of hypotheses (here the monotonicity or polynomial assumption) is no longer that simple and the number of factors increases. At this point, DoE helps in selecting the truly necessary experiments from the possible ones.
Fixed-size and sequential Design of Experiments
Solutions to this first problem have long existed in engineering, and there is already a corresponding selection of literature. However, these solutions have one thing in common: they generate so-called ‘fixed-size Designs of Experiments,’ i.e., experiment plans of a fixed size that match exactly the established hypotheses.
At the same time, the assumption is made that each time you are starting from scratch. Even when examining the tenth coffee machine, the DoE assumes that it is a completely new machine, and the effect of brewing time could be entirely different from the previous ones. All parameters are entirely new, and nothing can be learned from the old, related experiments.
Sequential Design of Experiments addresses exactly this assumption. The idea is to learn from old measurements. And how does a machine learner do that? With a model. For this to work, two things must be in place: first, a fixed-size DoE with which enough can be learned, and second, good model quality, which can be determined, for example, through cross-validation.
Sequential Design of Experiments: Active Learning vs. Bayesian optimization
Sequential Design of Experiments thus learns from already existing experimental data. The question now is, what should it learn? Two ideas are distinguished:
- Finding new points that improve the existing model, making it more accurate (e.g., what influence do grind size and brewing time have on coffee taste?)
- Finding new points that can estimate where the optimum lies (e.g., what grind size and brewing time are needed for the best coffee?)
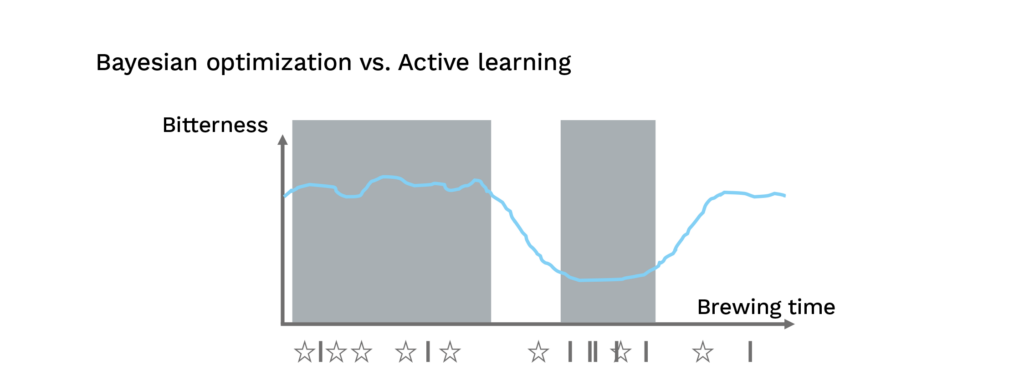
1) Active learning: concentrates successively on the interesting parts of the function, e.g. strong fluctuations, jumps (☆)
2) Bayesian optimization: concentrates successively on the minimum of the function (I)
These ideas differ fundamentally, as can be seen in the image above. The first idea is interested in factor areas where ‘a lot’ happens. Methods of Active Learning help to determine these areas and select the right points. The second idea is interested in factor areas where the function value is particularly optimal (low or high, depending on the user’s choice). Bayesian optimization can help here, for example.
The consequences of good Design of Experiments
Design of Experiments is thus a method that can generate the necessary data in research and development. It can reduce costs and resource waste, enabling ‘methodically intelligently’ research. In customer projects, we have already demonstrated that up to 50% of experiments can be saved using sequential DoE.
In the past, DoE helped to specify the influence of variables in ever-new problems. Today, it can learn from existing data to find interesting areas. It builds on Machine Learning models–and because it proposes new experiments independently, it is a true Artificial Intelligence.
Further information can be found in the associated literature:
Statistics for Experimenters: Design, Innovation, and Discovery (2nd Edition)
Box, G. E., Hunter, W. H., & Hunter, S., Wiley-Interscience, 2005, Link
Design and Analysis of Experiments (10th Edition)
Montgomery, D. C., Wiley, 2019, Link
The Design of Experiments Fisher, R. A., Nature 137, 252–254, 1936, Link
