
In einem weiteren Blogbeitrag dieser Serie haben wir die Lineare Regression kennengelernt. Wir haben gesehen, dass wir mit der Methode der kleinsten Quadrate (engl. Least Squares) eine Regressionsgerade an Trainingsdaten anpassen können, um für neue, unbekannte Datenpunkte einen Zielfunktionswert vorherzusagen. Wir konnten so für unser Anwendungsbeispiel eine Gerade finden, die uns intuitiv sinnvoll erschien:
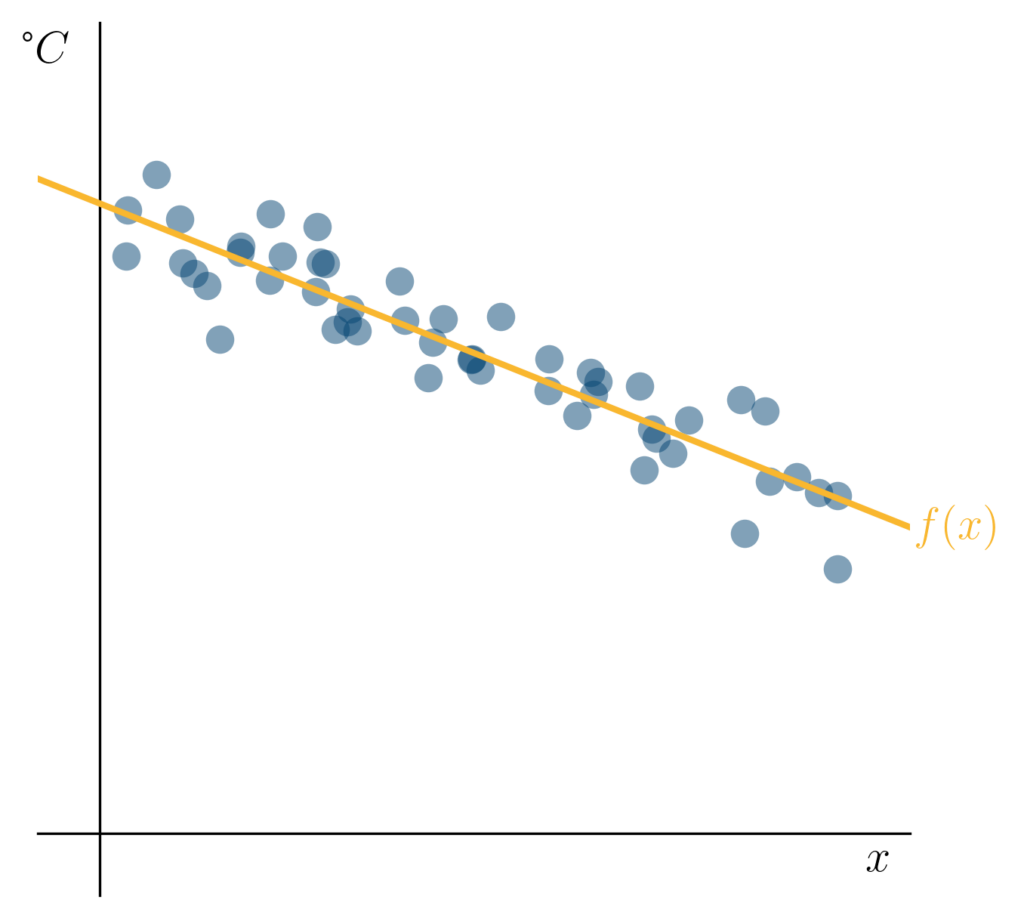
Auf der -Achse haben wir die Einstellungen des Temperaturreglers eines Kühlschranks aufgetragen und auf der -Achse die gemessenen Temperaturen.
Nehmen wir an, dass unsere Daten einem Versuch entstammen, in dem wir für verschiedene Einstellungen am Temperaturregler unseres Kühlschranks die Temperatur in diesem gemessen haben. Hier erscheint es sinnvoll, dass ein linearer Zusammenhang besteht (je höher die Reglerstufe, desto kälter der Kühlschrank). Es ist nachvollziehbar, dass mehrere unabhängige Temperaturmessungen bei derselben Einstellung nicht exakt dasselbe Ergebnis liefern. Dieses leichten Schwankungen sind ganz normal und man bezeichnet sie als Rauschen.
Unser obiges Beispiel zeigt dieses Rauschen sehr schön.
Ausreißer und Probleme beim Training
Manchmal kann es jedoch sein, dass einige Messungen misslingen. Im folgenden Bild haben wir drei weitere Messungen vorgenommen.
Wir sehen die drei Punkte, die nicht dem Trend der übrigen Messungen folgen, am rechten oberen Rand der Darstellung. Solche Datenpunkte nennen wir Ausreißer. Ausreißer können in unserem Kühlschrank entstehen, wenn etwa das Thermometer nicht richtig funktioniert oder eine Messung nicht richtig durchgeführt wird (zum Beispiel, wenn die Tür zu lang offen steht).
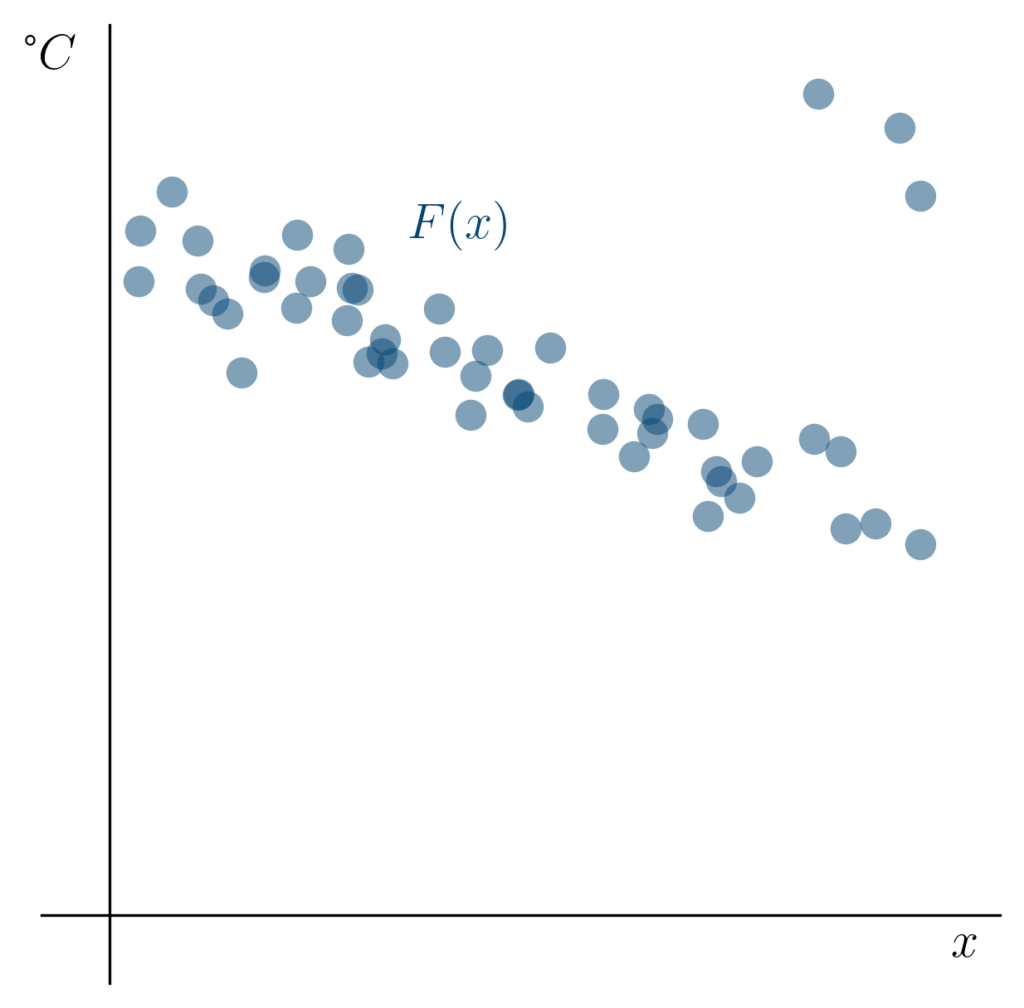
Wir würden uns von unserem Lernverfahren wünschen, dass es trotz der Präsenz solcher Ausreißer den globalen Trend der Daten identifiziert.
Wenn wir jedoch das Verfahren der kleinsten Quadrate zum Training auf diesen Daten verwenden, um eine Gerade [latex]f_{LSQ}(x)[/latex] zu bestimmen, erhalten wir das folgende Ergebnis:
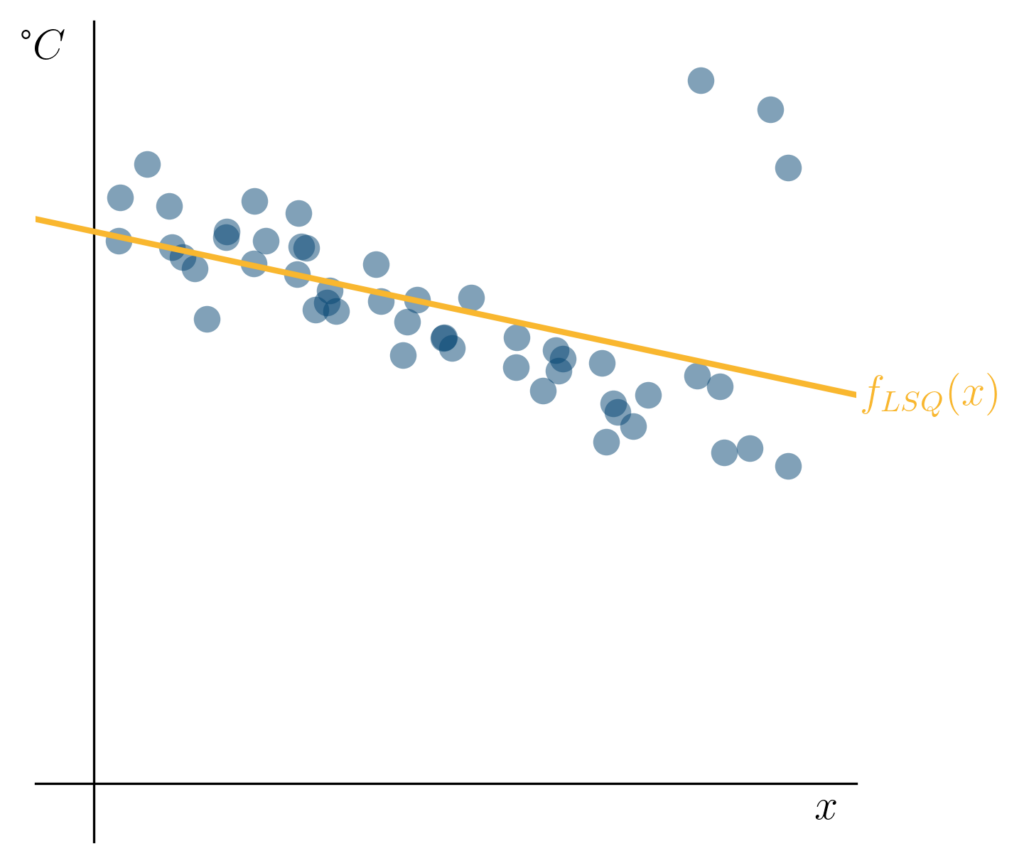
Die Methode der kleinsten Quadrate reagiert empfindlich auf unsere drei Ausreißer.
Unsere Regressionsgerade
[latex]f_{LSQ}(x)[/latex]
wird hier scheinbar von den drei Ausreißern „angezogen“. Wir können vermuten, dass unsere Vorhersagen über die Temperatur in unserem Kühlschrank für hohe Einstellungswerte unseres Reglers nicht mehr gut sein werden.
Wir wollen uns nun damit beschäftigen, woran dieses Verhalten liegt und wie man es (teilweise) beheben kann.
Robuste Lineare Regression mit kleinster Absoluter Abweichung
Im vorherigen Blogbeitrag haben wir gesehen, dass das Verfahren der kleinsten Quadrate die folgende Fehlerfunktion minimiert:
[latex] E_{LSQ}(a,b) = sum_{x text{ in Trainingsmenge}} left( a cdot x + b – F(x) right)^2 [/latex]
Der Abstand [latex]a cdot x + b – F(x)[/latex] unserer Trainingspunkte [latex]x[/latex] von der Regressionsgerade, die durch die Parameter [latex]a[/latex] und [latex]b[/latex] beschrieben wird, geht hier quadratisch in die Fehlerfunktion ein. Das bedeutet, dass die „Kosten“, die wir für Trainingspunkte „bezahlen“, die weit von unserer Regressionsgeraden entfernt liegen, sehr hoch sind. Sie wachsen nicht nur linear, sondern quadratisch. Daher kommt es in unserem Beispiel dazu, dass es günstiger ist, die kleinen Abstände vieler Punkte zu unserer Geraden etwas zu vergrößern, um den großen Abstand weniger Punkte etwas zu verringern.
Es gibt viele verschiedene Möglichkeiten, unsere Gerade robuster an die Daten anzupassen. Eines dieser Verfahren verwendet die Methode der kleinsten absoluten Abweichung (engl. least absolute deviations)}, die die Fehlerfunktion
[latex] E_{LAD}(a,b) = sum_{x text{ in Trainingsmenge}} left| a cdot x + b – F(x) right| [/latex] minimiert. Diese Fehlerfunktion betrachtet, anstatt des quadrierten Abstands zur Geraden, den „normalen“ (Euklidischen) Abstand. Wenn wir nun ein Verfahren verwenden, das diese Fehlerfunktion minimiert, erhalten wir auf unseren Trainingsdaten folgende Regressionsgerade [latex]f_{LAD}(x)[/latex]:
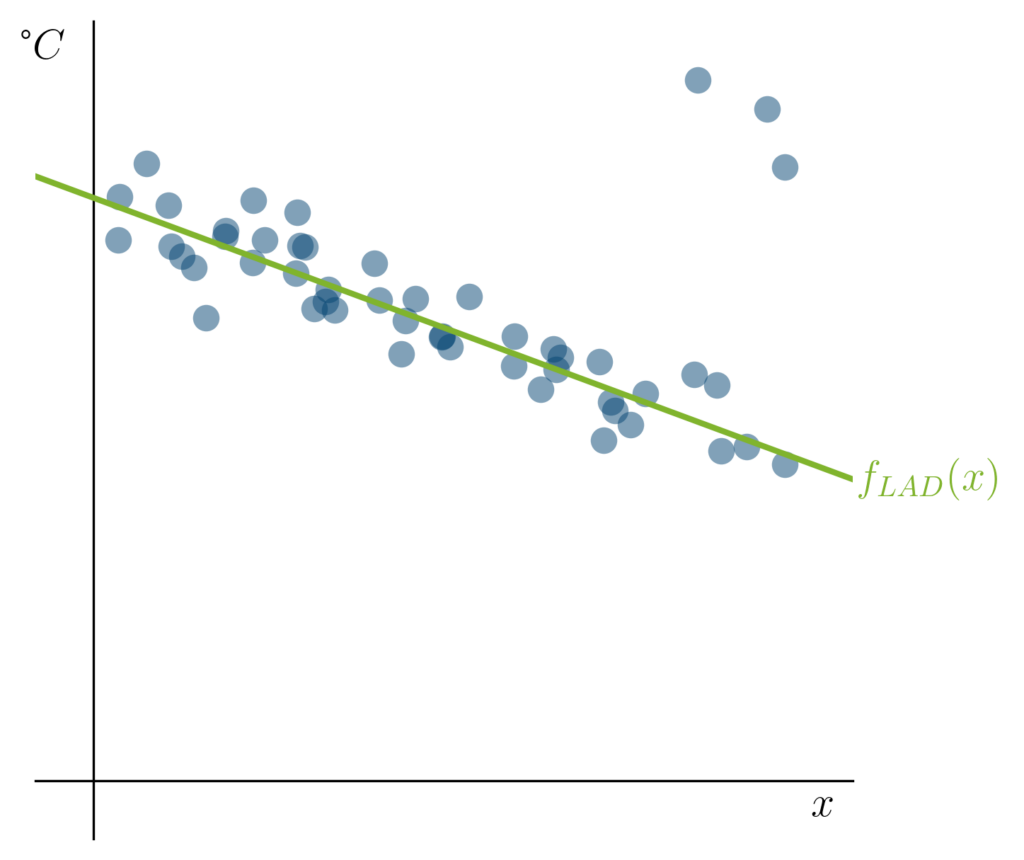
Durch eine Veränderung unserer Fehlerfunktion haben wir also erreicht, dass die Gerade [latex]f_{LAD}(x)[/latex], die diese Fehlerfunktion minimiert, unserer Erwartung wieder entspricht. Interessanterweise ist die Idee, Lineare Modelle mit der Methode der kleinsten absoluten Abweichung an Daten anzupassen, bereits sehr alt: Sie geht mindestens auf Boscovich (1757) und Laplace (1793) zurück. Dies bedeutet, dass sie schon länger bekannt ist, als die besser bekannte Methode der kleinsten Quadrate, die von Gauss (1801) und Legendre (1805) beschrieben wurde.
Warum nutzen wir also üblicherweise die Methode der kleinsten Quadrate, wenn sie doch beim Vorliegen von Ausreißern versagt? Die Antwort hierauf ist, dass die Optimierung von [latex]E_{LAD}[/latex] aufwändiger ist, als die Optimierung von [latex]E_{LSQ}[/latex]. Dies liegt daran, dass für die Minimierung von [latex]E_{LAD}[/latex] nur iterative Verfahren bekannt sind, die in der Regel viele Rechenschritte benötigen, um eine optimale Lösung zu finden. Für die optimale Lösung von [latex]E_{LSQ}[/latex] existiert hingegen eine einfache Formel. Wir wollen nun aber dennoch zeigen, wie wir ein gegen Ausreißer robustes Regressionsverfahren praktisch mit Hilfe von Python und den Paketen numpy und scipy umsetzen können.
Praktische Umsetzung einer Robusten Linearen Regression
Wir gehen im Folgenden wieder davon aus, dass wir eine beliebige Python Umgebung zur Verfügung haben, in der die Pakete Numpy und Scipy installiert sind. Zum Beispiel ein lokal oder auf google colab laufendes Jupyter Notebook. Beginnen wir mit dem Import von numpy, scipy und dem Laden unserer Daten, die als Textdatei vorliegen:
Die Optimierung von [latex]E_{LAD}[/latex] kann mithilfe von Linearer Optimierung umgesetzt werden. Im Kern geht es darum, ein System von (linearen) Ungleichungen aufzustellen, die definieren, welche Bedingungen unsere beiden Geradenparameter [latex]a[/latex] und [latex]b[/latex] erfüllen müssen und die Geradenparameter zu finden, die eine (lineare) Zielfunktion minimieren. Glücklicherweise kann unsere Fehlerfunktion [latex]E_{LAD}[/latex] genau in der notwendigen Weise dargestellt werden. Die Hintergründe zu den notwendigen Umformungen haben wir in zwei Beiträgen unserer Coding Nuggets Reihe dargestellt.
Die Variablen m und n stehen jeweils für die Dimensionalität und Anzahl der Messpunkte in unserem Datenset. Wir suchen nun nach dem Vektor vecW, der den Ausdruck vecW.T @ vecC minimiert, unter der Bedingung, dass der Vektor matA @ vecW zeilenweise nie größer als der Vektor vecB ist. Hierbei schreiben wir @ für die übliche Matrix-Vektor-Multiplikation. Eine Methode, die einen solchen Vektor [latex]vecW[/latex] identifiziert, ist bereits im Paket scipy.optimize implementiert und kann wie folgt aufgerufen werden:
Das Objekt result enthält neben unserem gesuchten Ergebnis noch weitere Informationen, auf die wir hier nicht genauer eingehen wollen.
Unsere gesuchten Geradenparameter können wir nun aber wie folgt auslesen:
Dies liefert uns die Parameter
[latex]
a = -0.371
b = 9.976 ,
[/latex]
die zugehörige Gerade [latex]f_{LAD}(x)[/latex] ist in Grün dargestellt.
Ausblick und weitere Details
In diesem Beitrag haben wir gesehen, wie wir eine Regressionsgerade mithilfe der Methode der kleinsten absoluten Abweichung bestimmen können. Diese Methode erlaubt eine größere Robustheit gegenüber Ausreißern in den Daten.
Wir haben gesehen, dass unsere angepasste Fehlerfunktion [latex]E_{LAD}[/latex] mithilfe von Linearer Optimierung gelöst werden kann und gezeigt, wie dies in Python praktisch umgesetzt werden kann. In unserer Coding Nuggets Reihe gehen wir in einem Artikel zur Robusten Linearen Regression genauer auf technische Details ein. Ein weiterer Artikel beleuchtet Grundlagen zu Linearer Optimierung in Python. Robuste Regression ist in der Praxis des Maschinellen Lernens hochrelevant und wird häufig im Kontext von Signalverarbeitung, Computer Vision und Wissensentdeckung verwendet.
