Recap: Was ist Decision Tree Pruning?
Mit Hilfe von Decision Trees (Entscheidungsbäumen) lassen sich praktisch und einfach Regeln basierend auf bereits vorhandenem Wissen oder Entscheidungsprozesse zur Klassifizierung darstellen. Da diese aber zu Overfitting neigen und bei wachsender Datenmenge sehr komplex und groß werden können, eignet sich die Verwendung von Pruningalgorithmen, um diesem Problem entgegenzuwirken. Hierbei werden redundante und für das Endergebnis unwichtige Unterscheidungen weggelassen, indem bestimmte Zweige im Baum entfernt werden, so dass der Baum kleiner und übersichtlicher bleibt. Wie das genau funktioniert, haben wie in diesem Blogpost beschrieben. Verschiedene Pruningalgorithmen unterscheiden sich beispielsweise in der Richtung, in welcher der Baum durchlaufen wird oder in ihrem Pruningkriterium, d.h. dem Kriterium, welches erfüllt werden muss, damit ein Zweig abgeschnitten wird. Im Folgenden werden wir zwei solcher Algorithmen näher betrachten und miteinander vergleichen.
Pessimistic Error Pruning (PEP)
Beim Pessimistic Error Pruning Algorithmus handelt es sich um einen Top-Down-Pruningalgorithmus. Das bedeutet, wir beginnen mit der Wurzel und überprüfen dann von oben nach unten für jeden Entscheidungsknoten, ob dieser relevant für das Endergebnis ist oder abgeschnitten werden sollte. Für jeden Knoten t berechnen wir dabei Folgendes:
- Den Fehler des Knotens e(t) errechnen wir als Summe der falsch zugeordneten Samples (d.h. Samples, die nicht der Mehrheitsklasse zugeordnet wurden) addiert mit einer Kontinuitätskorrektur von ½ im Fall von binären Entscheidungen. Dies machen wir, um einem Bias entgegenzuwirken, der entstehen kann, wenn das gleiche Set von Samples sowohl für das Erstellen als auch das Prunen eines Baums verwendet wird.
- Den Fehler des Subtrees des Knotens e(Tt) berechnen wir als Summe der Fehler aller aus dem Knoten t folgenen Blätter (inklusive der Kontinuitätskorrekturen).
- Den Standard Error berechnen wir nun aus diesen beiden Ergebnissen und n(t), was die Anzahl an Samples im Knoten t beschreibt:
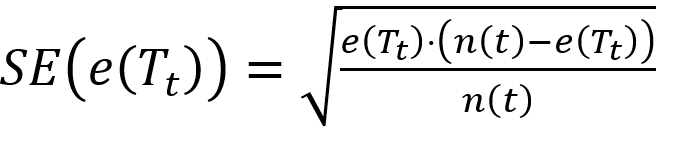
Gepruned wird nun, wenn die Summe aus Standard Error und Fehler des Subtrees größer oder gleich dem Fehler des Knotens ist. Der Knoten t macht dann nämlich als Blattknoten weniger Fehler als der Subtree.
Dies wird an folgendem Beispiel veranschaulicht:
Wir betrachten eine Datenbank, die verschiedene Arten von Iris-Blumen beinhaltet und diese anhand von deren verschiedenen Blütenblatt- und Kelchblattgrößen klassifiziert. Die 150 Blumen kann man dabei in drei Unterarten sortieren (Setosa, Virginica, Versicolor). Zuerst haben wir diese nun mithilfe eines Entscheidungsbaumes mithilfe der Attribute klassifiziert. Im Folgenden werden die beiden Algorithmen auf diesen Baum angewendet und es wird dann erklärt, was bei dem Pruning jeweils passiert.
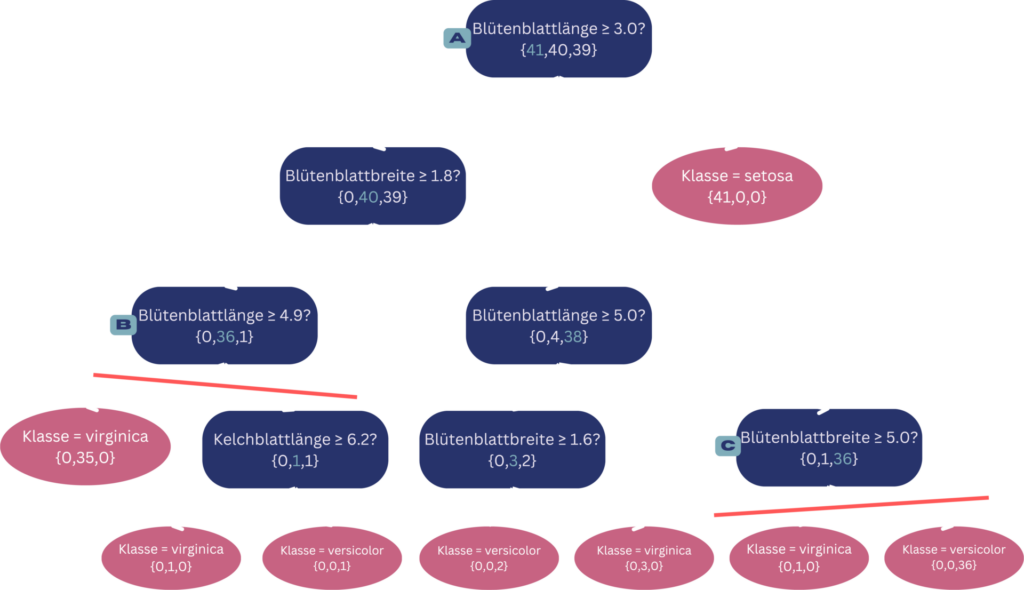
Entscheidungsbaum zur Klassifizierung von Iris-Blumen mit Entscheidungsknoten (blau) und Blattknoten (rot). Die roten Trennlinien stellen die durchgeführten Pruningschritte des Pessimistic Error Pruning Algorithmus dar.
© Michelle Fraund und Julia Wingenfeld
Für den Pessimistic Error Pruning Algorithmus (PEP) schauen wir uns dafür beispielhaft folgende 3 Knoten in dem dargestellten Baum an. Mit Knoten A sehen wir zuerst die Wurzel. Da es sich bei dem Algorithmus um einen Top-Down Algorithmus handelt, ist die Wurzel auch aus Sicht des Algorithmus der erste Knoten, der betrachtet wird. Da hier 40 + 39 = 79 Samples nicht der Mehrheitsklasse (blau markiert) zugeordnet wurden, erhalten wir einen Fehler von 79.5 (inklusive der Kontinuitätskorrektur) für den Wurzelknoten. Der Fehler des Subtrees beträgt beim Wurzelknoten 4, da wir von diesem insgesamt 8 Blattknoten erreichen können, die jeweils einen Fehler von 0 haben. Der Standarderror beträgt mit Einbezug der insgesamt 120 Samples, die im Wurzelknoten betrachtet werden, etwa 1.97. Da der Fehler des Wurzelknotens mit 79.5 also größer als die Summe aus dem Fehler des Subtrees und des Standarderrors (4 + 1.97 = 5.97) ist, ist das Pruningkriterium also nicht erfüllt und es wird nicht geprunt. Betrachten wir nun die beiden Knoten im Baum, die das Pruningkriterium erfüllen: Blattknoten B hat 1 von 37 falsch zugeordnete Samples, also einen Knoten-Fehler von 1.5, sowie 3 erreichbare Blattknoten mit jeweils einem Knoten-Fehler von 0, was einen Subtree-Fehler von 1.5 und einen Standarderror von etwa 1.19 ergibt. Somit ist das Pruningkriterium erfüllt, da der Knoten-Fehler kleiner als die Summe aus Subtree-Fehler und Standarderror ist (1.5 < 1.5 + 1.19). Bei Knoten C ist dies mit 1.5 < 1 + 0.99 ebenfalls der Fall. Bei den Knoten wird also jeweils geprunt, also die darunter liegenden Teilbäume abgeschnitten. Die Knoten werden dadurch zu Blattknoten. Durch diesen Vorgang wird der Baum nicht nur kompakter, sondern die Accuracy verbessert sich auch von 93% auf etwa 97%.
Minimum Error Pruning (MEP)
Der andere Algorithmus den wir betrachten, durchläuft den Baum andersherum (Bottom-Up). Der Baum wird von unten nach oben durchlaufen – also von den Blättern zu der Wurzel, wobei zusätzlich eine andere Formel verwendet wird, um unsere Knoten zu bewerten.
Das Grundprinzip ist hierbei, dass wir den Fehler von einem Elternknoten mit seinen Kinderknoten vergleichen. Dadurch prüfen wir, ob die Kinderknoten den Fehler verbessern werden oder nicht. Wenn die Kinder einen geringeren Fehler haben, tragen sie positiv zum Ergebnis bei und werden behalten. Wenn der Fehler der Kinder allerdings größer ist, wird durch sie das Ergebnis schlechter und die Kindknoten deswegen entfernt. Um den Fehler von dem Elternknoten zu berechnen, benutzen wir einen Parameter m, der ursprünglich den Einfluss von der a-priori Wahrscheinlichkeit pai, dass ein Sample nicht in einer bestimmten Klasse ist, bestimmt:
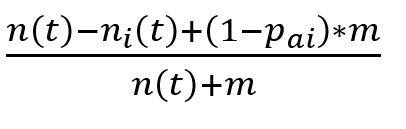
Zur Vereinfachung verwenden wir als pai einfach 1/Anzahl der Klassen k und für m ebenfalls die Anzahl der Klassen. Dadurch verschwindet die a-priori Wahrscheinlichkeit pai aus unserer Formel für die Berechnung des Fehlers:
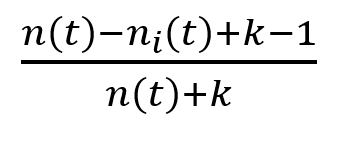
Um diesen Fehler mit dem von den Kindknoten vergleichen zu können, müssen wir die Fehler der Kinder miteinander verrechnen. Dabei ist es wichtig, dass der Knoten, der über mehr Samples entscheidet, auch mit einer höheren Gewichtung bewertet wird. Diese Gewichte bestimmen den Einfluss der jeweiligen Kindknoten. Das Gewicht beschreibt die Wahrscheinlichkeit, dass ein Sample in den jeweiligen Kindknoten geht. Wie anfangs schon erwähnt, muss jetzt der Fehler der Kinder größer sein als der des Elternknotens, damit wir den Subtree abschneiden können.
Nun wird dieses Prinzip an dem gleichen Baum demonstriert wie bei dem ersten Algorithmus:
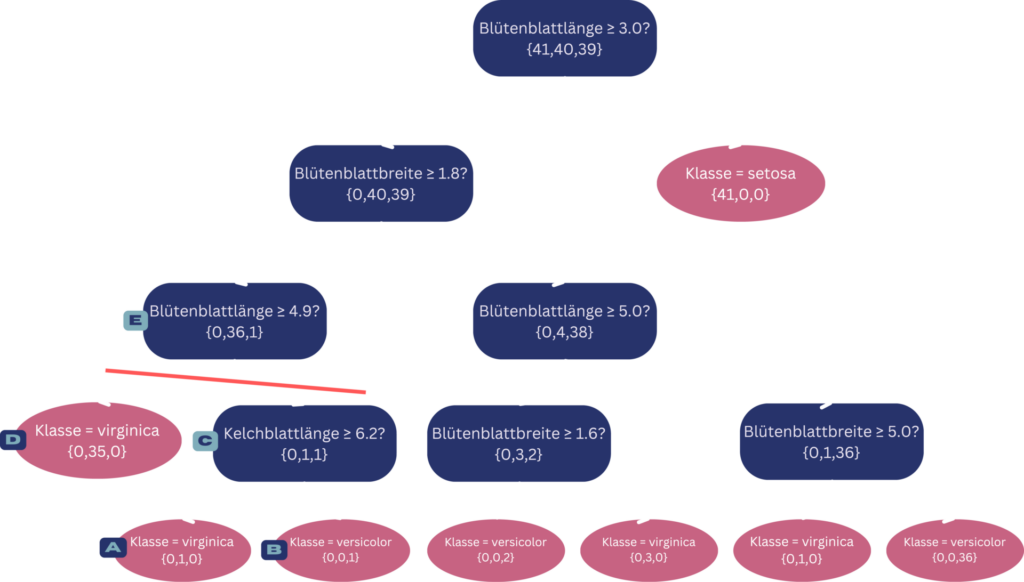
Entscheidungsbaum zur Klassifizierung von Iris-Blumen mit Entscheidungsknoten (blau) und Blattknoten (rot). Die rote Trennlinie stellt den durchgeführten Pruningschritt des Minimum Error Pruning Algorithmus dar.
© Michelle Fraund und Julia Wingenfeld
Da MEP ein Bottom-up Algorithmus ist, betrachten wir zuerst die Blattknoten, welche in der Abbildung mit A und B beschriftet sind. Um zu entscheiden, ob diese ein Teil des Baumes bleiben oder abgeschnitten werden, müssen wir ihren gemeinsamen gewichteten Fehler mit dem von dem Elternknoten vergleichen. Die Kinder haben beide jeweils das gleiche Gewicht und den gleichen Fehler, da beide ein Sample haben, was in dem jeweiligen Knoten richtig klassifiziert wird. Der gemeinsame Fehler lautet in dem Fall 1/2. Der Fehler von dem Elternknoten der beiden (Knoten C) ist 3/5. Dementsprechend wird der Fehler bei den Kindknoten A und C minimiert, weshalb diese im Baum bleiben.
Mit dem nächsten Schritt gehen wir einen Knoten höher und vergleichen nun Knoten D und C mit ihrem Elternknoten E. D und C haben jeweils einen Fehler von 0,082 und E einen Fehler von 0,075. In diesem Fall ist es jetzt also andersherum. Die Kinder des Knotens E verschlechtern den Fehler und sind deswegen unbrauchbar für unseren Entscheidungsbaum. Dementsprechend werden sie abgeschnitten und der Decision Tree verkleinert.
Die restlichen Abgleiche im Baum führen dazu, dass nicht weiter gepruned wird und unser Entscheidungsbaum ist damit fertig.
Vergleich der beiden Algorithmen
Beide Algorithmen haben dasselbe Grundprinzip, bei welchem die Bedeutung von Knoten bewertet werden. Der größte Unterschied ist die Bearbeitungsrichtung. Grundsätzlich gelten die Top-down Verfahren als risikoreicher, da wichtige Branches unkontrolliert abgeschnitten werden könnten. PEP sorgt in dem Fall durch das Pruningkriterium dafür, dass meistens in den richtigen Situationen und auch ausreichend gepruned wird. Auf der anderen Seite ist in der Minimum-Error-Algorithmus außerdem sehr vorsichtig und pruned vergleichsweise selten, weshalb kaum nennenswerte Verbesserungen eintreten. Dementsprechend ist der MEP-Algorithmus in den meisten Fällen die schlechtere Wahl, obwohl es sich um das risikoärmere Prinzip handelt.
Dies sieht man sehr anschaulich ich dem folgenden Beispiel:
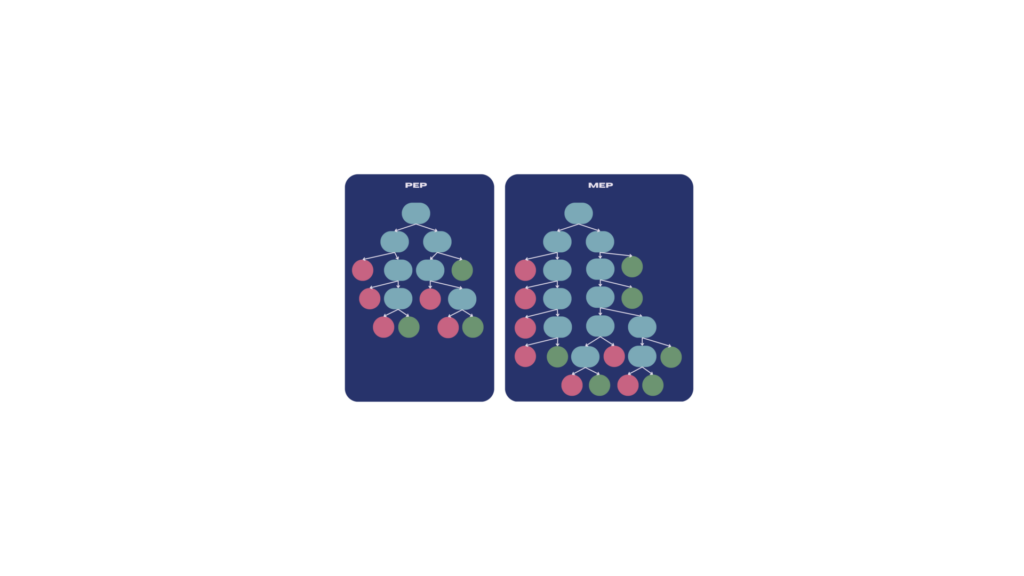
Grobe Darstellung zweier Entscheidungsbäume zur Veranschaulichung des Größenunterschieds nach Anwendung der beiden Pruningverfahren. Zu sehen sind Entscheidungsknoten basierend auf verschiedenen Attributen wie z.B. der Tumorgröße (blau) und die Blattknoten zur Klassifikation in gutartig (grün) und bösartig (rot).
© Michelle Fraund und Julia Wingenfeld
Es handelt sich hierbei um einen Datensatz zur Klassifikation von Brustkrebs, bei welchem anhand von verschiedenen Attributen wie beispielsweise der Größe oder Konkavität eines Tumors eine Einordnung in gutartige und bösartige Tumore ermittelt wird.
Die beiden Algorithmen können Entscheidungsbäume dieses Datensatzes kürzen. Als PEP auf einen Entscheidungsbaum dieses Datensatzes angewendet wird, wurde die Anzahl der Blätter von 19 auf 8 reduziert, was deutlich zeigt, dass der Baum übersichtlicher geworden ist. Zusätzlich ist die Fehlerrate geringer geworden, da von den Daten, auf denen der Baum getestet wurde, 2 zusätzliche Samples korrekt klassifiziert wurden.
MEP hat bei dem dort angewendeten Baum lediglich von 15 Blättern auf 13 gekürzt und hatte keine Verbesserung in der Fehlerrate. Dementsprechend stellen wir fest, dass auch bei diesem Datensatz PEP bessere Ergebnisse liefert.
Fazit
Abschließend kann man sehen, dass es sehr relevant sein kann, für welche Algorithmen man sich genau entscheidet, obwohl beide das gleiche Ziel haben. Kleinste Unterschiede in Algorithmen können einen Einfluss auf das Endergebnis haben, welches in unserem Fall bei dem Pessimistic-Error-Pruning Algorithmus definitiv besser ist. Allerdings ist es wichtig zu erwähnen, dass diese Algorithmen nicht die einzigen Pruning Algorithmen sind und für verschiedene Bäume/Anwendungen verschiedene Algorithmen in Frage kommen können. Es gilt also genau abzuwägen, welchen Algorithmus man für ein spezifisches Problem verwendet.
Verwendete Datasets:
Sowohl das Iris Dataset als auch das Brustkrebs Dataset, mit welchen wir die Entscheidungsbäume erstellt haben, stammen von scikit-learn:
Iris Blumen: https://scikit-learn.org/stable/auto_examples/datasets/plot_iris_dataset.html
Brustkrebs: https://scikit-learn.org/stable/modules/generated/sklearn.datasets.load_breast_cancer.html

