
In anderen Blogbeiträgen aus der Reihe Grundlagen des Maschinellen Lernens haben wir bereits gesehen, welche Arten des Maschinellen Lernens es gibt und dass Optimierung im Maschinellen Lernen eine Schlüsselposition einnimmt. In diesem Beitrag wollen wir uns konkret mit linearen Modellen beschäftigen, einer grundlegenden Modellklasse, die im überwachten Lernen angewandt werden kann. Lineare Modelle nehmen einen linearen Zusammenhang zwischen den beobachtbaren Daten und einem abhängigen Zielwert an. Lineare Regression ist das vermutlich am häufigsten eingesetzte Verfahren, um ein lineares Modell an Daten anzupassen und funktioniert schnell und recht zuverlässig auf großen sowie kleinen Datenmengen.
Im überwachten Lernen gehen wir davon aus, dass wir eine Menge von Trainingsdaten haben, für die wir den Wert einer Zielfunktion [latex]F[/latex] kennen.
Zum Beispiel könnten unsere Datenpunkte [latex]x[/latex] die Einstellungen am Temperaturregler unseres Kühlschranks sein und die Zielfunktionswerte [latex]F(x)[/latex] Messungen der Temperatur im Kühlschrank entsprechen.

Unsere Trainingsdaten: Temperaturmessungen ( ) in Grad Celsius für verschiedene Reglereinstellungen eines Kühlschranks.
In unserem Beispiel sind die Trainingsdaten reelle Zahlen, die wir auf der [latex]x[/latex]-Achse aufgetragen haben. Die Zielfunktionswerte, die wir für die Trainingsdaten kennen, haben wir auf der [latex]y[/latex]-Achse aufgetragen. Wir wollen nun [latex]F[/latex] „lernen“, um für neue Datenpunkte, die nicht aus unserer Trainingsmenge stammen, den Wert der Zielfunktion vorhersagen zu können. In unserem Beispiel wollen wir vielleicht abschätzen, wie kalt der Kühlschrank wird, wenn wir den Regler zum Beispiel auf zehn stellen.
Ein linearer Zusammenhang zwischen den Daten und den Zielfunktionswerten
Wenn wir die Daten in dem obigen Beispiel betrachten, können wir beobachten, dass vermutlich ein linearer Trend vorliegt: Je höher wir den Regler unseres Kühlschranks stellen, desto tiefer sinkt die Temperatur im Kühlschrank. Außerdem scheint es so, als könne man gut eine Gerade finden, die diesen Zusammenhang ungefähr beschreibt, zum Beispiel die folgende:
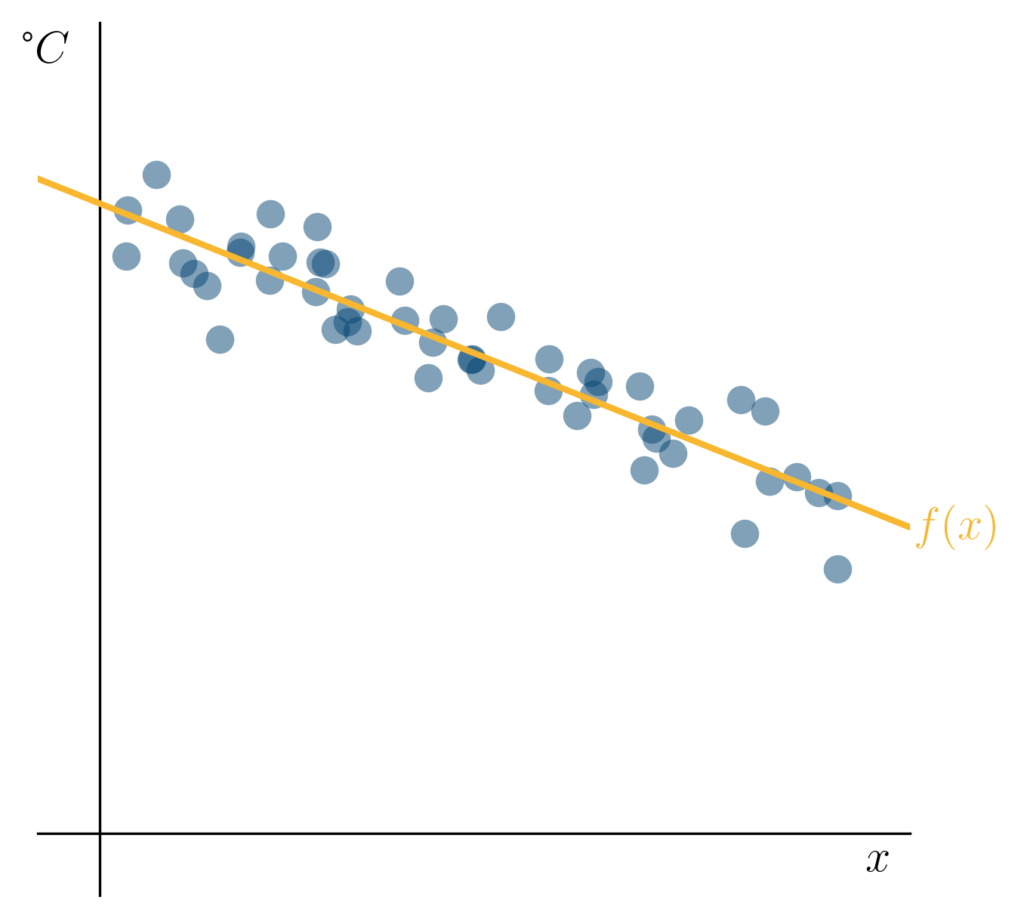
Eine intuitiv sinnvolle Funktion ( ), die den Zusammenhang zwischen den Reglereinstellungen und der gemessenen Temperatur ( ) beschreibt.
Wir wollen im Folgenden versuchen, eine solche Gerade zu finden, die unsere Trainingsbeispiele gut beschreibt. Eine Gerade wie in unserem Beispiel kann durch eine Geradengleichung [latex] f(x) = a cdot x + b [/latex] für reelle Zahlen [latex]a[/latex] und [latex]b[/latex] beschrieben werden. Hierbei beschreibt [latex]a[/latex] die Steigung der Geraden, und [latex]b[/latex] den Schnittpunkt mit der [latex]y[/latex]-Achse. Um nun für einen unbekannten Datenpunkt [latex]x'[/latex] einen Zielfunktionswert vorherzusagen, können wir [latex]x'[/latex] also einfach in unsere Geradengleichung einsetzen und [latex]f(x‘)[/latex] berechnen, wenn wir [latex]a[/latex] und [latex]b[/latex] kennen. Damit erhalten wir eine Vorhersage [latex]f(x‘)[/latex], die den uns unbekannten Zielfunktionswert [latex]F(x‘)[/latex] hoffentlich gut annähert.
Lineare Regression
Wir haben also unser Problem, den Zielfunktionswert für einen unbekannten Datenpunkt [latex]x'[/latex] vorherzusagen, darauf zurückgeführt, die Werte von [latex]a[/latex] und [latex]b[/latex] zu bestimmen. Lineare Regression ist eine Methode, die genau dies macht. Hierzu wendet sie das Verfahren der kleinsten Quadrate an. Ziel ist es unter den unendlich vielen Geraden, die man durch die Geradengleichung definieren kann, diejenige zu finden, die unsere Daten intuitiv richtig beschreibt. Das Verfahren der kleinsten Quadrate (engl. ‚Least Squares‘, LSQ) minimiert eine Fehlerfunktion [latex]E_{LSQ}[/latex], die den quadratischen Abstand all unserer Trainingspunkte von der Geraden beschreibt:
[latex]E_{LSQ}(a,b) = sum_{x text{in Trainingsmenge}} left( a cdot x + b – F(x) right)^2 [/latex]
Wir haben hier unsere Gerade durch ihre beiden Parameter [latex]a[/latex] und [latex]b[/latex] dargestellt und suchen nun die Gerade (beziehungsweise das [latex]a[/latex] und das [latex]b[/latex]), die [latex]E_{LSQ}[/latex] minimiert.
Wir werden nun sehen, wie wir dies in der Programmiersprache Python mit dem Paket Numpy erreichen können.
Praktische Umsetzung der Linearen Regression
Wir gehen im Folgenden davon aus, dass wir eine irgendwie geartete Python-Umgebung zur Verfügung haben, in der das Paket Numpy installiert ist. Zum Beispiel ein lokal oder auf google colab laufendes Jupyter Notebook. Daher beginnen wir mit dem Import von Numpy und dem Laden unserer Daten, die als Textdatei vorliegen:
Der Code erwartet, dass die Datei data.csv die reellen Trainingsdaten in der ersten Zeile enthält und die dazugehörigen Zielfunktionswerte in der zweiten Zeile. Demnach enthält nun vecX die Trainingsdaten und vecY die Zielfunktionswerte. Unsere Fehlerfunktion [latex]E_{LSQ}[/latex] können wir nun in Matrix-Vektor-Schreibweise wie folgt darstellen:
[latex]E_{LSQ}(a,b) = sum_{x text{ in Trainingsmenge}} left( (a,b) cdot left(begin{array}{c} x 1 end{array}right) – F(x)right)^2[/latex]
Das erlaubt uns, die nachfolgende Matrix zu definieren. Sie besteht aus einer Zeile, die unsere Datenpunkte enthält, gefolgt von einer Zeile, die nur Einsen enthält.
Die Methode der kleinsten Quadrate, die uns einen Vektor [latex]{vecW} = (a,b)[/latex] berechnet und unsere Fehlerfunktion [latex]E_{LSQ}[/latex] auf unseren Trainingsdaten minimiert, ist bereits im Numpy-Unterpaket „linalg“ implementiert und kann wie folgt aufgerufen werden.
Wir können nun also die Lineare Regression mithilfe der Methode der kleinsten Quadrate durchführen. Wie die Funktion [latex]f[/latex] und die Daten graphisch dargestellt werden können, kann der begleitenden Code Datei entnommen werden. Wir geben daher jetzt nur die beiden berechneten Geradenparameter aus:
Dies liefert uns
[latex]
a = -0.399
b = 10.099
[/latex]
Somit haben wir ein lineares Modell von unseren Trainingsdaten “gelernt„ und können diesen gelernten Zusammenhang auf verschiedene Weisen nutzen. Zum Beispiel können wir unsere gefundene Gerade anzeigen oder das Modell verwenden, um eine Vorhersage für die Temperatur in unserem Kühlschrank für eine bestimmte Reglereinstellung zu machen. Um eine Vorhersage für einen beliebigen Datenpunkt zu machen, können wir mit den Koeffizienten wie folgt verfahren:
Als Ergebnis erhalten wir für unseren Fall [latex] f(10) = 6.105 [/latex]
„@“ ist hier der Operator, der das Skalarprodukt zwischen zwei Vektoren ausrechnet, das in diesem Fall genau unserer Definition der Geradengleichung entspricht. Unsere Vorhersage können wir nun beliebig verwenden, oder einfach den Datenpunkt gemeinsam mit seinem Zielfunktionswert (in Gelb) anzeigen lassen.

Die von vorhergesagte Temperatur des Kühlschranks für die Reglereinstellung =10.
Ausblick
Wir haben ein einfaches maschinelles Lernverfahren kennen gelernt:
Lineare Regression mithilfe des Verfahrens der kleinsten Quadrate. Wir haben gesehen, wie man dieses Verfahren in Python auf eindimensionale Daten anwendet, um eine Gerade zu lernen, die unsere Daten gut beschreibt. Wir haben diese Gerade auch genutzt, um einen Zielfunktionswert für einen unbekannten Datenpunkt vorherzusagen. Wer gerne eine allgemeinere Formulierung dieses Verfahrens sehen möchte, dem sei unsere Reihe der ML2R Coding Nuggets ans Herz gelegt. In einem weiteren Blogbeitrag werden wir sehen, wie man ein robusteres Trainingsverfahren umsetzen kann, das auch dann gut funktioniert, wenn unsere Trainingsdaten einige Ausreißer enthalten.
