
Dieser Beitrag erklärt, was sich hinter dem Konzept der Klassifikation verbirgt und knüpft damit an Beiträge aus der Reihe über Grundlagen des Maschinellen Lernens (ML) an. Klassifikation ist ein Modellierungsansatz, ein Denkwerkzeug, um Probleme auf eine bestimmte Art darzustellen und so zu abstrahieren. Im Überblicksbeitrag zu den verschiedenen Arten des ML lernen wir, dass sich alle Fragen, die eine feste Menge an Antworten haben, als Klassifikationsprobleme darstellen lassen. Das Konzept der Klassifikation trägt so in unterschiedlichsten Bereichen zur Problemlösung bei: in der Bildverarbeitung autonomer Systeme, wie Roboter und in selbstfahrenden Autos, zur Unterstützung bei Diagnosen in der Medizin, beim Filtern von Daten in der Physik, zur Analyse von formellen und informellen Texten, wie gerichtliche Urteile, Bewerbungen, Produktrezensionen oder Social-Media-Posts, …
Doch wie funktioniert dieses fundamentale Werkzeug des Maschinellen Lernens? Erfahren Sie mehr im nachfolgenden Beitrag.
Was ist Klassifikation?
Klassifikation ist neben der Regression der zweite fundamentale Modellierungsansatz im überwachten Lernen. Klassifikation kann man als Zuordnung oder Gruppierung von Beobachtungen in vordefinierte Kategorien beschreiben. Kategorien bezeichnet man hier als Klassen, Beobachtungen formal als Datenpunkte. Das Programm oder die Funktion, welche die Zuordnung von Datenpunkten zu Klassen vornimmt, nennt sich Klassifikator. Das Label eines Datenpunkts enthält Informationen darüber, zu welcher Klasse der Klassifikator den Datenpunkt zugeordnet hat. Ging es bei der Regression darum, für einen Datenpunkt eine oder mehrere reelle Zahlen als Ausgabe zurückzugeben, so ist die Antwort eines Klassifikators auf eine relativ kleine Menge an diskreten Werten, den Klassen, begrenzt.
Ein Klassifikationsproblem ist wie ein Multiple-Choice-Test für den Computer, bei dem die Antwortmöglichkeiten immer gleich sind und sich die Fragen nur durch das konkret zu betrachtende Subjekt unterscheiden: Objektklassifikatoren beantworten zum Beispiel die Frage welches Objekt, aus einer Menge an möglichen Objekten (Antwortmöglichkeiten), auf einem bestimmten, gegebenen Bild (das konkrete Subjekt der Frage) zu sehen ist. Wie bei Multiple-Choice-Tests, werden auch bei der Modellierung von Klassifikationsproblemen bestimmte Arten von Fragen unterschieden.
Binäre Klassifikationprobleme: Bei dieser Art von Problemen gibt es nur zwei mögliche Antworten. Oft wird das Problem dann als Ja-Nein-Frage formuliert, indem man explizit das Zutreffen einer der Antworten abfragt.
Beispiel: Wie ist das Wetter? {Gut, Schlecht} → Ist das Wetter gut? {Ja, Nein}
Multi-Klassen Klassifikationsprobleme: In diesem Fall gibt es mehr als zwei Antwortmöglichkeiten, es wird aber nur nach einer Antwort verlangt. Dies ist der in der Praxis am häufigsten vorkommende Fall von Klassifikationsproblemen.
Beispiel: Was für ein Objekt befindet sich auf dem Bild? {Tier, Fahrzeug, Lebensmittel, Möbelstück, …}
Multi-Label Klassifikationsprobleme: In diesem Szenario gibt es auch mehr als zwei Antwortmöglichkeiten, diese schließen sich aber nicht gegenseitig aus. Der Klassifikator darf jedem Datenpunkt mehrere Label zuweisen.
Beispiel: Welche Diagnosen treffen auf einen Patienten zu? {Grippe, Knochenbruch, Entzündung, Vergiftung, …}

Klassifikation heißt Muster in Daten zu erkennen
Wie man anhand der in den obigen Beispielen gegebenen Klassen sehen kann, sind die Konzepte, die eine „Klasse“ repräsentieren soll, meist klar definierbar oder für einen Menschen intuitiv verständlich. Denn für uns Menschen ist klar, was ein Fahrzeug von einem Tier unterscheidet, wie ein Knochenbruch aussieht oder ob das Wetter eher gut oder eher schlecht ist. Wie aber bringen wir den Klassifikator dazu, Daten innerhalb dieser Kategorien zu erkennen und zu unterscheiden?
Klassifikation zählt zu den Ansätzen im überwachten Lernen. Bevor ein Klassifikator einsatzbereit ist, durchläuft er daher zunächst eine Trainingsphase. In dieser Phase verarbeitet er Trainingsdaten in Form von gelabelten Datenpunkten. Meist sind dies Datenpunkte, die von einem Menschen per Hand gelabelt wurden (mehr Informationen zum Training von Modellen finden Sie im Beitrag „Wie lernen Maschinen?„). Aufgabe der Entwickler:innen ist es sicherzustellen, dass es sich bei den Trainingsdaten um „gute“ Beispiele handelt. Dazu muss der Trainingsdatensatz möglichst unterschiedliche Beispiele für jede Klasse enthalten.
Während des Trainings lernt der Klassifikator durch die Beispiele eine Art indirekte Definition für jede Klasse. Er lernt, welche Charakteristika für eine bestimmte Klasse sprechen und welche nicht. Man spricht hierbei auch von Mustererkennung: Datenpunkte derselben Klasse haben mehr Muster gemeinsam als Datenpunkte unterschiedlicher Klassen.
Dadurch lernt der Klassifikator nicht notwendigerweise eine „vollständige“ Definition einer Klasse, sondern nur so viel wie nötig ist, um die Klassen voneinander zu unterscheiden.
Feature-Engineering: Das Aussehen eines Datenpunkts definieren
Schauen wir uns nun an, was ein „Datenpunkt“ genau ist. Beim Feature-Engineering legen Entwickler:innen fest, welche Informationen in einem Datenpunkt vorhanden sein sollen und wie (Roh-)Daten weiterverarbeitet werden müssen, bevor sie dem Klassifikator präsentiert werden. Die Entwickler:innen müssen sicherstellen, dass die Daten alle Informationen enthalten, die nötig sind, um die Aufgabe zu lösen. Damit ist das Feature Engineering nicht nur bei der Entwicklung von Klassifikationssystemen wichtig, sondern in allen Bereichen des Maschinellen Lernens.
Um Klassifikationsaufgaben lösen zu können, muss jeder Datenpunkt genügend Informationen enthalten, um ihn eindeutig einer bestimmten Klasse zuordnen zu können. Er sollte aber auch nicht zu viele Informationen beinhalten, denn dies kann unbeabsichtigte Nebeneffekte haben und es dem Klassifikator erschweren, die zur Klassifikation relevanten Informationen zu erkennen.
Formen klassifizieren
Um das grundlegende Konzept der Klassifikation weitergehend zu erläutern, stellen wir uns nun – in Anlehnung an den Beitrag über die verschiedenen Arten des Maschinellen Lernens – folgende Aufgabe:
„Kategorisiere die Figuren auf der folgenden Abbildung nach ihrer Form:“
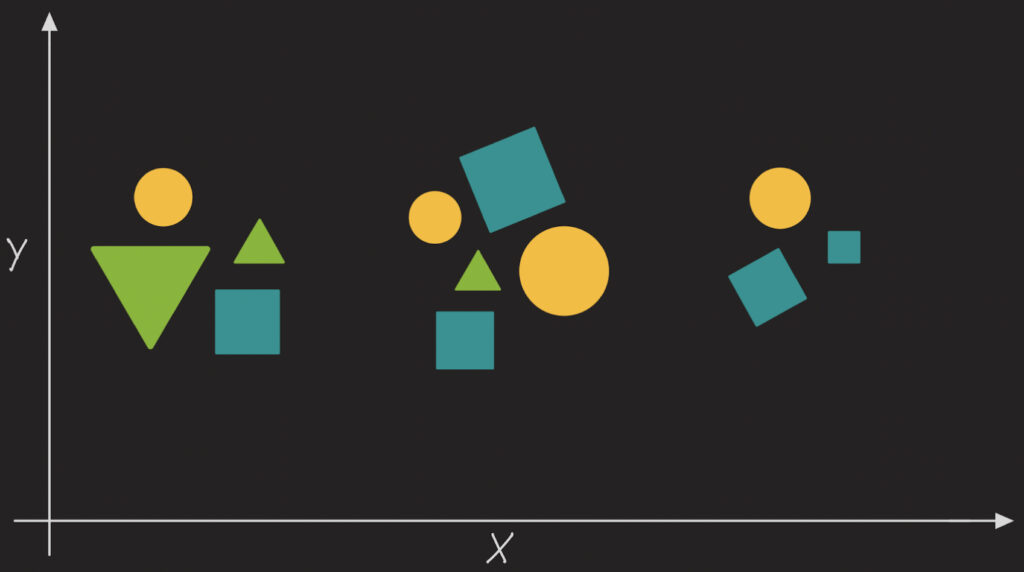
Zunächst stellen wir fest, dass auf dem Bild drei unterschiedliche Formen zu sehen sind. Geben wir den Klassen die Namen „Kreis“, „Dreieck“ und „Quadrat“.
Damit der Computer etwas mit dem Begriff „Figur“ anfangen kann, müssen wir ihm das Objekt, welches er kategorisieren soll, beschreiben. In der Praxis gibt es hierfür meist bereits eine Datengrundlage. Sagen wir, dass wir in unserem Fall für jede Figur folgende Feature (Eigenschaften) zur Verfügung gestellt bekommen:
Figur = [X-Koordinate, Y-Koordinate, Farbe, Anzahl Kanten, Anzahl Ecken]
Die Reihenfolge, in der die Feature hier aufgelistet sind, ist für jede Figur immer dieselbe.
Repräsentation finden
Wäre diese Liste an Features bereits eine gute Repräsentation einer „Form“ als Datenpunkt?
Schauen wir genauer hin: Die Features „X-Koordinate“ und „Y-Koordinate“ sind für die Fragestellung nicht von Nutzen, denn es besteht kein Zusammenhang zwischen Position und Form der Figur. Das Feature „Farbe“ sieht vielversprechender aus: Alle Dreiecke sind grün, alle Kreise orange und alle Quadrate türkis. Andererseits können wir uns aber auch einen grünen Kreis vorstellen. Einen solchen beobachten wir zwar nicht in den Daten, aber unsere Lebenserfahrung sagt uns, dass Form und Farbe nicht notwendigerweise zusammenhängen.
Bleiben noch die Feature „Anzahl Kanten“ und „Anzahl Ecken“. Mit diesen Features können wir alle Figuren eindeutig ihrer Form zuordnen. So hat etwa ein Quadrat sowohl vier Kanten als auch vier Ecken. Hiermit vermeiden wir das Problem, welches sich mit dem Feature „Farbe“ ergab – denn kein Quadrat wird jemals mehr oder weniger als vier Ecken oder Kanten haben. Damit sind wir theoretisch fertig, aber eine Sache fällt uns noch auf: Die Anzahl der Kanten und Ecken eignet sich jeweils gleich gut zur Klassifikation, die Information ist in diesem Sinne redundant. In diesem Fall könnte es passieren, dass der Klassifikator lernt, Dreiecke aufgrund der Anzahl an Ecken und Quadrate aufgrund der Anzahl der Kanten zu erkennen. Das ist nicht falsch und wird auch immer zur richtigen Klassifikation führen, in der Praxis würde man sich aber dazu entscheiden nur eines von mehreren redundanten Features zu behalten.
Als Vorverarbeitung der Rohdaten entfernen wir also fünf der sechs gegebenen Features. Damit ist unsere finale Repräsentation einer Form als Datenpunkt:
[Anzahl Kanten]
Die Klassifikationsfunktion definieren
Um die Aufgabe abzuschließen, müssen wir nun noch die Klassifikationsfunktion definieren, welche die erarbeitete Repräsentation nutzt. Eine mögliche Funktion ließe sich über folgende drei Regeln definieren:
- ordne einem Objekt mit einer Kante die Klasse „Kreis“ zu,
- ordne einem Objekt mit drei Kanten die Klasse „Dreieck“ zu, und
- ordne einem Objekt, das weder eine noch drei Kanten hat, die Klasse „Quadrat“ zu.
Die letzte Regel verdeutlicht die Annahme, dass wir nicht davon ausgehen, eine Figur mit genau zwei oder mehr als vier Kanten zu beobachten.
Damit haben wir nun für unser einfaches Beispiel „von Hand“ eine geeignete Repräsentation für unsere Datenpunkte gefunden und ebenfalls „von Hand“ einen einfachen, regelbasierten Klassifikator definiert.
Klassifikation in der Praxis
Sowohl das Feature-Engineering als auch das Finden einer Klassifikationsfunktion geschieht in der Praxis natürlich nicht von Hand. Im Vergleich zu unserem Beispiel, sind die Datensätze in der Praxis viel größer und die Zusammenhänge der Feature viel komplexer. Deshalb verwenden Entwickler:innen beim Feature-Engineering statistische und visuelle Analysewerkzeuge. Nach dieser Analyse müssen Entwickler:innen dann entscheiden, welche Modellklasse am geeignetsten erscheint, die Aufgabe zu lösen. Sie entscheiden hierbei, welche Art von Klassifikationsfunktion nun der oben erwähnten Trainingsphase unterzogen werden soll. Bekannte Beispiele für Modellklassen sind etwa Neuronale Netze, Support Vector Machines, Naive-Bayes, Entscheidungsbäume oder k-Nächste-Nachbarn.
Jede Modellklasse bringt in der Praxis, je nach Anwendungsfall, unterschiedliche Vor- und Nachteile mit sich. So sind Neuronale Netze zwar sehr gut darin, einen Großteil des Feature-Engineerings selbst zu übernehmen, ihre Tainingsphase dauert jedoch oft länger und es werden vergleichsweise große Mengen an Trainingsdaten benötigt.
Klassifikation als Denkwerkzeug im Maschinellen Lernen
Zusammenfassend können wir festhalten: Klassifikation stellt ein Problem als das Zuordnen von Daten zu verschiedenen Klassen dar. Es wird dabei zwischen binären, multi-Klassen und multi-Label Problemen unterschieden. Klassifikatoren begreifen die semantischen Konzepte hinter Klassen nicht direkt über eine Definition, sondern indirekt, indem sie lernen Muster in den Daten zu erkennen und voneinander zu unterscheiden. Beim Feature-Engineering geht es darum, eine Darstellung der Daten zu finden, die es dem Klassifikator ermöglicht, charakteristische Muster in den Daten möglichst leicht zu finden und zu erlernen.
Die Klassifikation wird in einer Vielzahl von Anwendungen des Maschinellen Lernens eingesetzt. Diese Artikel unseres ML-Blogs präsentieren exemplarisch Algorithmen, die sich als Klassifikatoren eignen, oder besprechen praxisnahe Probleme, welche mit Hilfe von Klassifikatoren gelöst werden:
- Convolutional Neural Networks in der Bildklassifikation
- Convolutional Neural Networks zur Gesichtserkennung
- Rekurrente Neuronale Netze im Finanzsektor
- Neuronale Netze in der Astronomie
- Neuronale Netze zur Urteilstextanalyse
- Support Vector Machines um Krankheitsverläufe besser einzuschätzen
- Rekurrente Neuronale Netze zur Widerspruchserkennung in Aussagen
