Das aktuell dominierende Verfahren zum Trainieren von Modellen des Maschinellen Lernens (ML) ist der Gradientenabstieg. So erlaubte das Backpropagation-Verfahren die Millionen von Parametern tiefer neuronaler Netze effektiv zu trainieren. Es war somit ausschlaggebend für die neue Blütezeit dieser Modellklasse. Dabei werden Gradienten – schulmathematisch auch Ableitungen genannt – der Loss-Funktion aller Neuronen nacheinander durch die Schichten des Netzwerks hinweg berechnet, beginnend mit der letzten Schicht. Dieses konzeptionell einfache Verfahren lässt sich recht problemlos implementieren und kommt mit grundlegendsten Rechenoperatoren aus. Heute ist der Begriff Training im Kontext von Maschinellem Lernen fast schon synonym zum Gradientenabstieg. Dabei gibt es andere Methoden, Modelle zu optimieren, unter anderem Evolutionäre Optimierung, die gegenüber gradientenbasierten Verfahren Vorteile bieten.
Das Training von ML-Modellen ist nämlich schlicht ein Optimierungsproblem (Optimierung im Maschinellen Lernen): Gegeben ist ein Datensatz [latex]mathcal{D}[/latex], beispielsweise mit Paaren [latex](x,y)[/latex] von Eingaben [latex]x[/latex] und erwarteten Ausgaben [latex]y[/latex]. Ist [latex]y[/latex] kontinuierlich, zum Beispiel in Form einer reellen Zahl, spricht man von einer Regression. Ist [latex]y[/latex] hingegen ein symbolischer Wert aus einer endlichen Menge, zum Beispiel Katze aus der Menge {Hund, Katze, Pferd}, spricht man von Klassifikation. Ein Modell [latex]mathcal{M}[/latex] mit Parametern [latex]theta[/latex] ist in der Lage, Eingaben [latex]x[/latex] auf [latex]y[/latex] abzubilden, dargestellt durch
[latex]mathcal{M}{theta}(x)=hat{y}[/latex]
Dabei bezeichnet [latex]hat{y}[/latex] die Vorhersage des Modells, im Gegensatz zum wahren Wert [latex]y[/latex], der durch den Datensatz vorgegeben ist. Beim Training suchen wir nun den optimalen Parameter
[latex]theta^[/latex]
, der dafür sorgt, dass die Modellausgabe für alle [latex]x[/latex] aus [latex]mathcal{D}[/latex] möglichst nah an der wahren Ausgabe [latex]y[/latex] liegt:
[latex]sum{(x,y)inmathcal{D}} d(y,mathcal{M}_{theta^}(x))~rightarrow ~min[/latex]
Dabei ist [latex]d(cdot,cdot)[/latex] ein beliebiges Distanzmaß, im Fall einer Regression zum Beispiel [latex]d(y,hat{y})=(y-hat{y})^2[/latex]. Die Summe im obigen Beispiel wird auch als Loss-Funktion [latex]L[/latex] bezeichnet.
Gradientenverfahren versuchen, diese Funktion zu minimieren, indem sie die Ableitung [latex]mathrm{d}L/mathrm{d}theta[/latex] bilden. Die Berechnung der Ableitung ist häufig rechenaufwendig. Außerdem kann [latex]L[/latex] viele unterschiedliche lokale Optima besitzen, oder sogar überhaupt nicht ableitbar sein. In diesem Fall können Gradientenverfahren entweder nicht effektiv oder gar nicht zum Einsatz kommen. Abhilfe schafft in diesem Fall die Evolutionäre Optimierung.
Optimierung durch lokale Suche
Nehmen wir eine noch allgemeinere Formulierung eines Optimierungsproblems als Grundlage: Aus einer Menge [latex]mathcal{X}[/latex] möglicher Lösungskandidaten soll ein Element
[latex]x^inmathcal{X}[/latex]
gefunden werden, das bezüglich einer festen Loss-Funktion [latex]L:~mathcal{X}rightarrowmathbb{R}[/latex] minimal ist:
[latex]x^=underset{xinmathcal{X}}{argmin}L(x)[/latex]
Grundsätzlich könnte das optimale Element [latex]x^*[/latex] durch Ziehen zufälliger Elemente aus [latex]mathcal{X}[/latex] gefunden werden. Dieser Random-Search-Ansatz ist zwar einfach umzusetzen, aber ineffektiv, wenn der Suchraum [latex]mathcal{X}[/latex] sehr groß ist. Er bildet dennoch eine gute Referenz, gegen die andere Verfahren verglichen werden können: Liefert ein Optimierungsverfahren schlechtere Ergebnisse als Random Search, ist es nicht geeignet für das vorliegende Problem. Im Gegensatz zum Gradientenverfahren, das sich ausgehend von einem Startpunkt [latex]x^t[/latex] in entgegengesetzte Richtung des Gradienten, [latex]-etacdotmathrm{d}L/mathrm{d}x^t[/latex] mit Schrittweite [latex]eta[/latex], bewegt, um sich möglichst direkt einem Optimum zu nähern, springt Random Search wahllos im Lösungsraum umher und testet zufällige Lösungskandidaten aus.
Ein Mittelweg besteht darin, von einem Startpunkt [latex]x^0[/latex] auszugehen und sich in der Umgebung dieses Punktes vorzutasten. Beispielsweise werden verschiedene nahegelegene Punkte [latex]tilde{x}^0_1,dots,tilde{x}^0_{lambda}[/latex] ausgewertet. Der Punkt mit dem niedrigsten Loss-Wert, welcher folglich näher am Optimum zu liegen scheint und daher am vielversprechendsten ist, wird sodann als neuer Ausgangspunkt [latex]x^1[/latex] übernommen. Ist keine der nahegelegenen Lösungen besser als der Ausgangspunkt, wird [latex]x^1=x^0[/latex] belassen. Wiederholt man diesen Vorgang häufig, so bewegt sich der Punkt [latex]x^t[/latex] für ein immer größeres [latex]t[/latex] auf ein Optimum zu. Dieses Schema bildet ein Optimierungsverfahren namens (1+λ)-EA. Dabei steht EA für Evolutionärer Algorithmus.
Evolutionäre Algorithmen
Die Evolutionären Algorithmen bilden eine Klasse von Optimierungsverfahren, die bereits seit den 1950er-Jahren erforscht werden. Das Vorbild ist dabei die erstmals von Charles Darwin formulierte Evolution in der Natur: Bei der Fortpflanzung von Lebewesen werden Gene der Eltern rekombiniert. Zusätzlich treten Mutationen auf, wodurch die Nachkommen Eigenschaften der Eltern erben und sich spontan neue Eigenschaften ausbilden können. Besser angepasste Nachkommen überleben und schaffen es, selbst Nachkommen zu zeugen. Schlechter angepasste Individuen sterben hingegen durch den Selektionsdruck, der zum Beispiel durch Fressfeinde oder begrenztes Nahrungsangebot entsteht. Dieser Vorgang wird bei den Evolutionären Algorithmen imitiert: Aus einer Population von [latex]mu[/latex] Eltern [latex][x^t_1,dots,x^t_{mu}][/latex] aus [latex]mathcal{X}[/latex] werden [latex]lambda[/latex] Nachkommen durch Rekombination und Mutation erstellt. Wie diese Operationen genau aussehen, hängt von dem Suchraum [latex]mathcal{X}[/latex] ab. Sind die Individuen beispielsweise wie Listen oder Vektoren aufgebaut, [latex]mathcal{X}=mathbb{Y}^n[/latex], so könnten zwei Vektoren [latex]boldsymbol{a}[/latex] und [latex]boldsymbol{b}[/latex] rekombiniert werden, indem sie vor einem zufällig gewählten Index [latex]minlbrace 1,dots,nrbrace[/latex] zerteilt werden und je ein Teil von jedem Elternteil übernommen wird: [latex]tilde{x}=(a_1,dots,a_{m-1},b_m,dots,b_n)[/latex]
Sind die Individuen reelle Zahlen, [latex]mathcal{X}=mathbb{R}[/latex], kann eine Mutation durch Addieren eines zufälligen, zum Beispiel normalverteilten, Rauschens erfolgen: [latex]tilde{x}=x+epsilon, ~epsilonsimmathcal{N}(0,1)[/latex]
Aus der gesamten Population, bestehend aus den [latex]mu[/latex] Eltern und den [latex]lambda[/latex] rekombinierten und mutierten Nachkommen, werden nun die [latex]mu[/latex] besten Individuen bezüglich der Loss-Funktion [latex]L[/latex] selektiert. Die Funktion bewertet sozusagen, wie gut angepasst ein Individuum ist. Sie wird daher im Kontext von Evolutionären Algorithmen Fitness-Funktion genannt und maximiert statt minimiert. Die [latex]mu[/latex] Individuen mit den niedrigsten [latex]L[/latex]-Werten (beziehungsweise der höchsten Fitness) bilden die nächste Elterngeneration, dann beginnt der Prozess von vorn. Erfüllt der Mutationsoperator bestimmte statistische Eigenschaften, ist es garantiert, dass die Population mit wachsender Zahl Generationen zum globalen Optimum [latex]x^*[/latex] konvergiert (Convergence of evolutionary algorithms in general search spaces).
Evolutionäre Optimierung von Quantenschaltkreisen
In dem neuen Paper Gradient-free quantum optimization on NISQ devices nutzen Forscher des ML2R Evolutionäre Algorithmen, um Schaltkreise von Quantencomputern zu optimieren. Die Schaltkreise sind zusammengesetzt aus verschiedenartigen Gates (Gattern), die auf einzelne oder auf Paare von Qubits wirken und reellwertige Parameter mit Werten zwischen [latex]0[/latex] und [latex]2pi[/latex] enthalten. Wird ein solcher Schaltkreis ausgeführt, ändert er den gemeinsamen Zustand der Qubits, und es entstehen Verschränkungen. Diese Verschränkungen für Berechnungen und insbesondere das Maschinelle Lernen nutzbar zu machen, ist Gegenstand aktueller Forschung.
Der Suchraum [latex]mathcal{X}[/latex] des vorliegenden Optimierungsproblems ist also die Menge aller Quantenschaltkreise, die sich aus allen Kombinationen von Gattern und Parametern ergibt. Potentiell können beliebig viele Gatter verwendet werden, daher ist [latex]mathcal{X}[/latex] eine unendliche Menge. Die Loss-Funktion [latex]L[/latex] ordnet einem Quantenschaltkreis einen reellen Wert zu und ist definiert als erwartete Kosten bezüglich einer Hamiltonian, die einem Quantenzustand eine Energie zuordnet. Einen Schaltkreis zu finden, der minimal bezüglich einer gegebenen Hamiltonian ist, ist ein schwieriges Problem der Physik, das von zentraler Bedeutung für die Erforschung von Quantenalgorithmen ist. Es ist eng verwandt mit dem Problem, effizient automatisiert einen Quantenschaltkreis zu finden, der eine bestimmte vorgegebene Funktionalität ausführt.
Sind die Gatter und deren Positionen in einem Quantenschaltkreis fest vorgegeben, können mit einem Gradientenverfahren die reellwertigen Gatterparameter optimiert werden. Für die Gatterstruktur selbst hingegen ist dies nicht möglich, denn das bloße Vorhandensein eines Gatters, beziehungsweise dessen Typ und Position, kann man nicht numerisch ableiten. Die Forschenden entschieden sich daher für den Einsatz Evolutionärer Algorithmen. Diese bieten große Flexibilität, da es genügt, die Rekombinations- und Mutationsoperatoren festzulegen, um zu garantieren, dass das Verfahren ein gutes Ergebnis findet. Zur Mutation eines Quantenschaltkreises werden hier beispielsweise zufällig Gatter hinzugeführt, entfernt, gegen andere Gatter ausgetauscht oder die Parameter leicht verändert. Durch solche kleinen Veränderungen wird der optimale Schaltkreis nach und nach über die Generationen hinweg konstruiert.
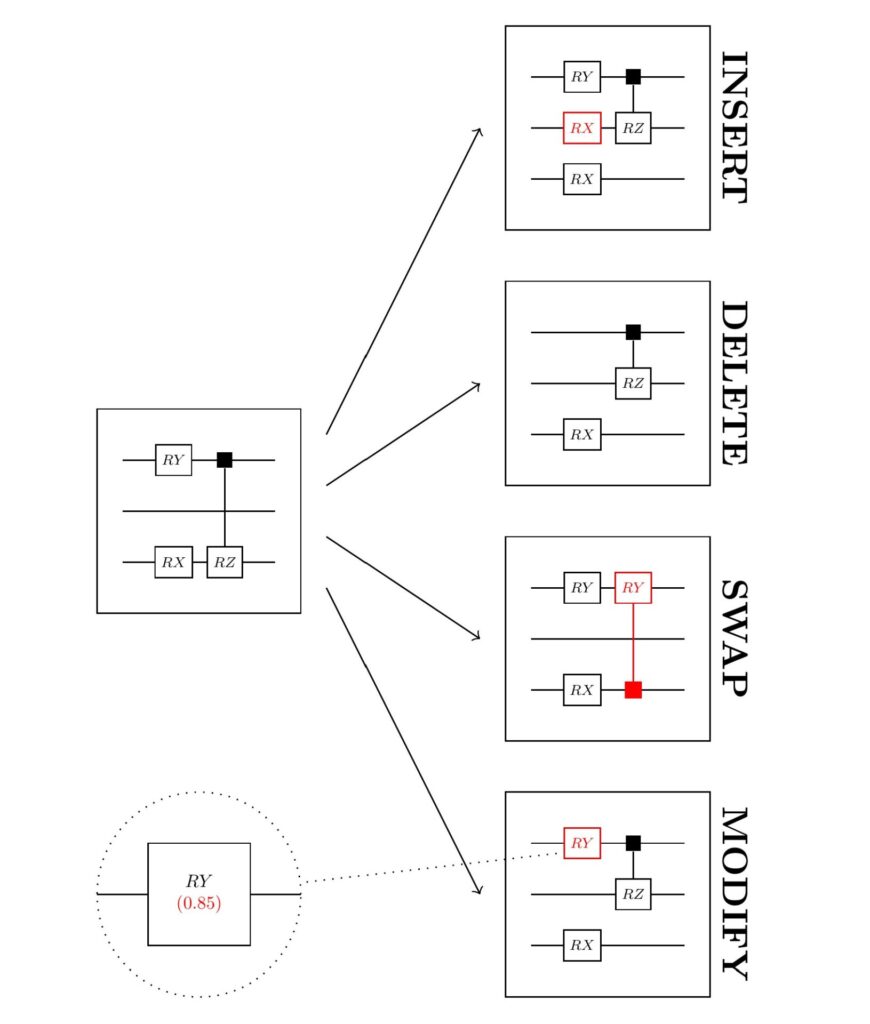
Schematische Darstellung der Mutation eines Ausgangsquantenschaltkreises (links) und der resultierenden Nachkommen (rechts). Nachkommen entstehen durch Einfügen, Löschen, Austauschen oder Verändern von Gattern.
In ihrem Paper konnten die Forschenden diesen Prozess nicht nur simulieren, sondern auf echten Quantencomputern mit bis zu 20 Qubits erfolgreich durchführen. Sie zeigten somit, dass Evolutionäre Optimierung effektiv anstelle der üblichen Gradientenverfahren für Probleme des Quantencomputings eingesetzt werden kann. Dadurch können nicht nur Parameter fester Gatterstrukturen gelernt, sondern auch kompaktere Quantenschaltkreise gefunden werden, die weniger Gatter benötigen.
Die untenstehende Graphik zeigt den Optimierungsverlauf auf verschiedenen Quantencomputern von IBM und in einer Simulation. In allen Fällen ist zu beobachten, dass die Energie im Verlauf der Generationen des evolutionären Algorithmus’ abnimmt, somit also eine gute Lösung schrittweise angenähert wird.

Performanz des Evolutionären Algorithmus’ auf 10 Qubits, ausgeführt auf mehreren Quantencomputern (farbige Linien) und simuliert (gestrichelte Linie).
Auch über ein halbes Jahrhundert nach ihrer Entwicklung erweist sich die evolutionäre Optimierung noch immer als flexibles und mächtiges Werkzeug für hochaktuelle Anwendungen. So auch im Quantum-Computing, wo gradientenbasierte Verfahren an ihre Grenzen stoßen.
Weitere Informationen im zugehörigen Paper:
Gradient-free quantum optimization on NISQ devices Lukas Franken, Bogdan Georgiev, Sascha Mücke, Moritz Wolter, Nico Piatkowski, Christian Bauckhage. Arxiv, 2020, PDF.
