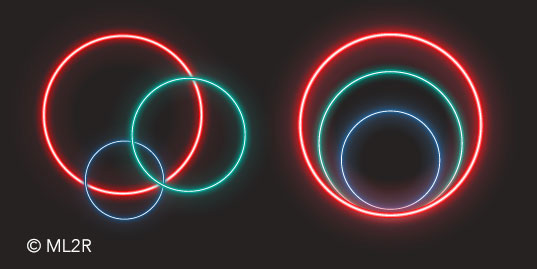
Daten sind wichtig für das Maschinelle Lernen. Wegen der potenziellen Auswirkungen auf die Gesellschaft, haben insbesondere die Big Data Technologien für große Aufregung gesorgt. Dabei kann Big Data metaphorisch als Treibstoff für die Rakete des Maschinellen Lernens verstanden werden. Eine Rakete kann ohne Treibstoff nicht fliegen. Aber, wäre es möglich, wenn man genug Treibstoff für die Rakete hat, jeden beliebigen Zielort zu erreichen?
Der Syllogismus, die einfachste Form der symbolischen logischen Schlussfolgerung, ist eine mathematische Darstellung des Denkens. Wie Syllogismen genau von neuronalen Netzen ausgeführt werden können, ist noch eine offene Frage für die Forschung der Künstlichen Intelligenz und des Maschinellen Lernens. Überraschenderweise ist es nicht möglich, maschinelle Lernsysteme alle Syllogismen Typen lernen zu lassen, egal wie viele Trainingsdaten es gibt. Grundsätzlich werden Trainingsdaten verwendet, um Assoziationen zwischen der Eingabe und Ausgabe herzustellen. Jedoch schwächt bei Syllogismen die Assoziation eines Typs die Assoziation eines anderen Typs ab. Eine Abhilfe besteht darin, auf das Lernen assoziativer Beziehungen zu verzichten und stattdessen eine sinnvolle Repräsentation der Bedeutung der Eingabe zu lernen.
Mit Trainingsdaten Syllogismen lernen
Ein Syllogismus beschreibt einen Katalog logischer Schlüsse und besteht immer aus zwei Prämissen, die zu einer Schlussfolgerung führen. Das zugrundeliegende Prinzip soll an folgendem Beispiel erklärt werden: Gegeben der zwei Prämissen (1) alle Griechen sind Menschen und (2) alle Menschen sind sterblich, schließen wir, dass alle Griechen sterblich sind.
Grundsätzlich hat die Aussage eines Syllogismus vier Formate: (1) alle X sind Y, (2) kein X ist Y, (3) manche X sind Y, (4) manche X sind nicht Y. Die Kombinationen dieser vier Formate in Prämissen und Konklusion ergibt 24 unterschiedliche Syllogismus-Strukturen zur Entscheidungsfindung. Die Frage, die sich hierbei stellt, ist: Kann ein maschinelles Lernsystem diese 24 einfachen Entscheidungsfindungsprozesse erlernen, wenn ausreichend Trainingsdaten vorhanden sind?

Ein überwachtes neuronales Netzwerk mit Euler-Diagrammen als Eingabe und einem symbolischen Vektor als Ausgabe
Um diese Frage zu beantworten, haben Forschende ein neuronales Netzwerk erzeugt und mit genügend Trainingsdaten trainiert (siehe Abstract Diagrammatic Reasoning with Multiplex Graph Networks, Investigating diagrammatic reasoning with deep neural networks). Insgesamt trainierten sie das neuronale Netzwerk mit 88.000 Syllogismus-Aufgaben und konnten eine Genauigkeit (Accuracy) von 99,8% für 8.000 neue Syllogismus-Aufgaben erreichen. Die obenstehende Abbildung zeigt die Architektur des Netzwerks. Die Eingabe des neuronalen Netzes sind zwei Euler-Diagramme. Alle möglichen Kombinationen der Euler-Diagramme erschöpfen die Typen der Syllogismen und assoziieren Eingaben mit logischen Schlussfolgerungen. Diese Methode leidet jedoch unter zwei Einschränkungen:
- Trainingsdaten können nicht gleichzeitig konsistente Relationen und logische Schlussfolgerung mit der Eingabe assoziieren: Obwohl das System weiß, dass alle Griechen sterblich sind, ist es gleichzeitig nicht sicher, ob manche Griechen sterblich sind.
- Eine einzelne Kombination zweier Euler-Diagramme kann die jeweilige Behauptung nicht darstellen. Das wollen wir mit folgendem Beispiel näher erklären: Aus der graphischen Kombinationen “manche Politiker sind Staatsmänner” (Überschneidung) und “keine Politiker sind Sportler” (Abtrennung) ergeben sich drei mögliche Behauptungen: (1) manche Staatsmänner sind Sportler, (2) keine Staatsmänner sind Sportler, (3) alle Sportler sind Staatsmänner. Doch die richtige syllogistische Behauptung wäre: Manche Staatsmänner sind keine Sportler.

Die graphische Kombination von “A überschneidet B” und “A trennt C ab” ergibt drei Möglichkeiten zwischen B und C: “B überschneidet C”, “B trennt C ab”, “C ist Teil von B”.
Syllogismus lernen: Trainingsdaten allein reichen nicht
Im Gegensatz zu dem oben beschriebenen Ansatz mit Trainingsdaten, glauben wir intuitiv, dass die zwei Eingaben/Prämissen genug Informationen für die Schlussfolgerung enthalten. Deshalb sollten weitere Trainingsdaten nicht erforderlich sein. Um dies zu untersuchen, haben wir ein neues neuronales Netzwerk entwickelt, um Euler-Diagramme für die beiden symbolischen Aussagen als Eingabe zu erstellen. Die untenstehende Abbildung zeigt: Das unüberwachte Netzwerk repräsentiert jede Entität in der Aussage als Kugeln im hochdimensionalen Raum und lernt ein Euler-Diagramm, dass die Bedeutung der beiden Eingaben genau erfasst. Der Wahrheitswert einer Schlussfolgerung wird durch die Inspektion des Euler-Diagramms bestimmt. Dies führt zu einer neuartigen maschinellen Lernmethode, die Bedeutungen der Eingaben einbettet, anstatt assoziative Beziehungen zwischen der Eingabe und der Ausgabe aufzubauen. In Experimenten erreichte dieses neuronale Netzwerk eine Genauigkeit (Accuracy) von 100% für die gleichen 14.000 Syllogismus-Aufgaben, die alle 24 Typen der Syllogismen abdecken.

Ein neues, unüberwachtes neuronales Netzwerk lernt ein Euler-Diagramm als die Repräsentation der Bedeutung der Eingaben.
Doch würde ein überwachtes neuronales Netzwerk die gleiche Genauigkeit haben wie unser oben beschriebener Ansatz? Die Güte des im ML2R entwickelten Verfahrens zeigt sich auch im Vergleich mit anderen ML-Ansätzen zum Erlernen von Syllogismen. So erreichte ein von Forscher D. Wang entwickeltes überwachtes neuronales Netz, welches Trainingsdaten verwendet, lediglich eine Genauigkeit von 76% für die gleichen 14.000 Aufgaben. Die Fehleranalyse zeigt, dass die Trainingsdaten nicht alle 24 Typen der Syllogismen abdecken können. Basierend auf diesem neuronalen Netz, das mit Daten trainiert wurde, kann ein System einerseits so trainiert werden, dass es lernt: Wenn alle X Y sind und alle Y Z sind, dann sind auch alle X Z. Andererseits kann ein System mit Trainingsdaten so trainiert werden, dass es folgendes lernt: Wenn alle X Y sind, und alle Y Z sind, dann sind einige X Z. Jedoch kann es nicht beide Schlussfolgerungen gleichzeitig erlernen. Die zwei Assoziationen schwächen sich gegenseitig ab, wie in der untenstehenden Grafik dargestellt. In einem unüberwachten neuronalem Netzwerk, welches im Rahmen unserer Studie entwickelt wurde, werden solche Fälle jedoch nicht auftreten, da es alle syllogistische Strukturen genau darstellen kann.

Wir haben gesehen, dass, unabhängig davon wie groß die Trainingsdaten sind, es kein überwachtes neuronales Netzwerk gibt, das alle 24 Syllogismus-Typen schlussfolgern kann. Das Vorhandensein des sprichwörtlichen Treibstoffes für Maschinelles Lernen alleine ermöglicht daher keine beliebige Zielerreichung. Stattdessen legt die gemeinsame Forschung nahe, dass durch unüberwachte neuronale Netzwerke eine semantische Repräsentation präzise erlernt werden kann, solange sie eine räumliche Konfiguration hat. Das von uns entwickelte unüberwachte neuronale Netz konstruiert hierbei eine räumliche Struktur für beliebige syllogistische Eingaben. So kann die Bedeutung der Eingaben aller Syllogismen gelernt werden. Hier stellen wir die Euler-Diagramme als die Repräsentation der Bedeutung dar.
Die Richtigkeit der gelernten Euler-Diagramme garantiert die Schlussfolgerung der Syllogismen und erklärt die Fehler. Unsere Experimente an Syllogismen zeigen, dass dieses unüberwachte neuronale Netzwerk die Genauigkeit der symbolischen logischen Schlussfolgerung fast erreicht. Damit versuchen wir eine neue Sichtweise auf vertrauenswürdige KI und erklärbare KI zu geben und schaffen Struktur, wo Daten machtlos sind.
Mehr Informationen in der zugehörigen Publikation:
T. Dong, C. Li, C. Bauckhage, J. Li, S. Wrobel, A. B. Cremers: Learning Syllogism with Euler Neural-Networks. 2020, PDF.
