Sum-Product Networks (SPNs) sind eine Art von probabilistischen graphischen Modellen (PGMs). Sie bestehen also aus Knoten, die durch Kanten miteinander verbunden sind, und repräsentieren Verteilungsfunktionen. So weit unterscheiden sie sich also nicht weiter von anderen PGMs wie beispielsweise Bayes- oder Markov-Netzen. Der wesentliche Unterschied besteht in der Semantik der einzelnen Knoten. Ein SPN ist ein sogenannter tripartiter Graph. Das bedeutet, dass es drei verschiedene Typen von Knoten gibt. Als Blattknoten werden alle Knoten in einem SPN bezeichnet, die keine ausgehenden Kanten besitzen. Diese repräsentieren univariate Verteilungsfunktionen, also Verteilungen, die genau über eine Variable definiert sind. Alle inneren Knoten eines SPNs sind entweder Summen- oder Produktknoten. Daher auch der Name Sum-Product Networks. Summenknoten repräsentieren Mischverteilungen, die sich als gewichtete Summe der Verteilungen ergeben, die durch die direkt folgenden Knoten, Kindknoten genannt, dargestellt werden. Produktknoten repräsentieren Faktorisierungen, die sich analog zu den Summenknoten als Produkt der durch die Kindknoten dargestellten Verteilungen ergeben.
Durch die Kombination von univariaten Verteilungen, Faktorisierungen und Mischverteilungen lassen sich schließlich beliebig komplexe Verteilungsfunktionen darstellen. Diese lassen sich für die verschiedensten Aufgaben, wie beispielsweise Bildsegmentierung, die Verarbeitung natürlicher Sprache oder sogar in der Robotik verwenden.
Abbildung 1: Darstellung der drei Knotentypen. Die beiden Abbildungen links stellen Blattknoten dar. Hierbei unterscheidet man zwischen Blattknoten für kategorische und kontinuierliche Variablen.
Wie trainiert man ein SPN?
Das Training eines SPNs folgt einem einfachen, aber effektivem Schema namens „LearnSPN“, das sowohl die Modellstruktur als auch dessen Parameter lernt. LearnSPN erstellt die Modellstruktur rekursiv, in dem für die Erstellung eines jeden Knoten aus fünf Operationen gewählt werden kann: SplitData, SplitVariables, SplitUninformativeVariables, NaiveFactorization und CreateLeaf.
SplitData erstellt einen Summenknoten und partitioniert den Datensatz unter Verwendung eines Clustering-Algorithmus wie zum Beispiel [latex]k[/latex]-Means. Für jede so entstandene Partitionsmenge wird rekursiv ein sub-SPN trainiert. Diese sub-SPNs bilden dann die Kindknoten des erstellten Summenknotens. Die Kantengewichte werden proportional zur Anzahl der Daten in den Partitionsmengen gewählt, sodass sie in der Summe 1 ergeben.
SplitVariables erstellt einen Produktknoten und partitioniert die Variablen mithilfe einer Unabhängigkeitsanalyse, sodass alle Variablen in einer Partitionsmenge abhängig voneinander und gleichzeitig möglichst unabhängig zu denen der anderen Partitionsmengen sind. Für jede der Partitionsmengen wird dann erneut ein sub-SPN trainiert. Hierbei werden jeweils nur die Daten in Bezug auf die Variablen der jeweiligen Partitionsmenge betrachtet.
Durch das Aufteilen der Daten und Variablen kann es vorkommen, dass Variablen ihren informativen Mehrwert verlieren und „uninformativ“ werden, sprich, alle Datenpunkte nehmen für bestimmte Variablen denselben Wert an. In solchen Fällen sorgt die Operation SplitUninformativeVariables für die Abspaltung dieser Variablen. Dazu wird ein Produktknoten erstellt, der für jede dieser Variable einen Blattknoten als Kind erhält. Die übrigen informativen Variablen werden dann in einem sub-SPN für das weitere Training verwendet.
Ein Spezialfall von SplitUninformativeVariables stellt die naive Faktorisierung dar, genannt NaiveFactorization. Hierbei wird ein Produktknoten erstellt, der für jede Variable einen Blattknoten erhält.
Zu guter Letzt dient die Operation CreateLeaf dazu, einen Blattknoten für eine Variable zu erstellen und anhand der gegebenen Datenpunkte eine univariate Verteilung zu schätzen. Die Art der Verteilung ist abhängig von der Variablen selbst.
Der Entscheidungsprozess, der bestimmt, welche Operation gewählt wird, ist in Abbildung 2 graphisch dargestellt. Ausschlaggebend sind dabei die Anzahl der Variablen [latex]|V|[/latex], die Existenz von Variablen ohne großen informativen Mehrwert, Clustern und Unabhängigkeiten sowie die Anzahl der Datenpunkte [latex]|X|[/latex], die einen gewissen Grenzwert [latex]t[/latex] nicht unterschreiten sollte. Sobald dieser Grenzwert unterschritten wird, werden keine weiteren Aufteilungen der Daten oder Variablen (nur SplitVariables) vorgenommen. Dadurch wird sichergestellt, dass die Anzahl der Datenpunkte in den Blättern ausreichend für eine sinnvolle Schätzung der Verteilungen ist.
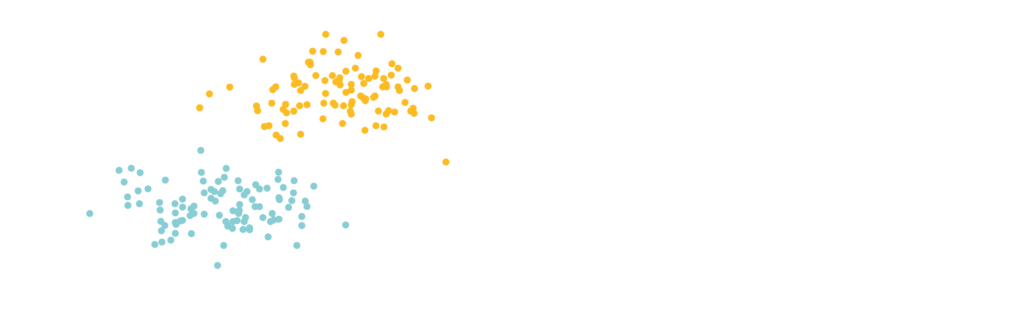
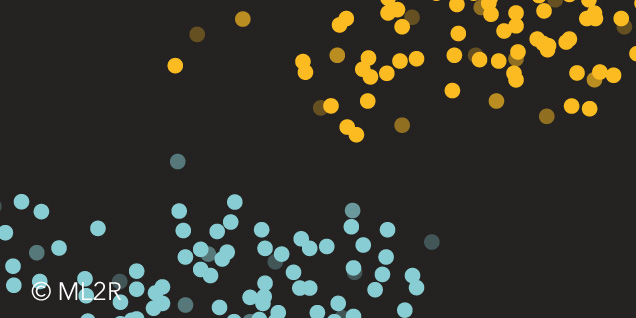
Abbildung 2: Links ist der Entscheidungsprozess während des Trainings mit LearnSPN und rechts der Trainingsdatensatz bestehenden aus zwei Clustern und ein darauf trainiertes SPN dargestellt.
Am Wurzelknoten werden zunächst die beiden Datencluster (blau und orange) getrennt. Anschließend werden für beide Cluster die Klassenzugehörigkeitsvariable [latex]C[/latex] abgespalten, da diese unter Betrachtung eines einzelnen Clusters ohne informativen Mehrwert ist. Da [latex]C[/latex] eine kategorische Variable ist, stellen die korrespondierenden Blätter Indikatoren der jeweiligen Klasse dar. Zum Schluss werden die beiden Koordinaten [latex]X[/latex] und [latex]Y[/latex] faktorisiert und aus den Daten Normalverteilungen geschätzt.
Inferenzen: Das trainierte KI-Modell in die Anwendung bringen
Nach dem Training eines SPNs soll dieses natürlich auch zur Vorhersage von bestimmten Zielgrößen, verwendet werden, welche für gewöhnlich als Inferenz bezeichnet wird. In der Anwendung von SPNs werden in der Regel drei Arten von Inferenzen unterschieden: Maximum a-posteriori (MAP), most probable explanation (MPE) und maximum likelihood (MAX).
Der grundlegende Unterschied zwischen den verschiedenen Inferenzarten liegt in der Unterteilung der Variablen in beobachtete Variablen, versteckte Variablen und Zielvariablen. Die beobachteten Variablen sind, wie der Name es bereits vermuten lässt, diejenigen Variablen, die wir beobachten können, beziehungsweise als Evidenz verwenden wollen, um schließlich die Zielvariablen vorherzusagen. Alle übrigen Variablen in unserem SPN bezeichnen wir als versteckte Variablen.
Die MAP-Inferenz sucht nach der wahrscheinlichsten Belegung unserer Zielvariablen, gegeben der beobachteten Variablen (Evidenz).
Existieren keine versteckten Variablen, sprich, alle nicht beobachteten Variablen sind Zielvariablen, so spricht man von einer MPE-Inferenz. Diese stellt also lediglich einen Spezialfall der MAP-Inferenz dar. Diese Art der Inferenz kann beispielsweise für klassische Klassifikationen verwendet werden.
Die MAX-Inferenz sucht nach der wahrscheinlichsten Belegung aller Variablen. Hierbei wird nicht weiter zwischen den Variablenarten unterschieden.
Betrachten wir im Folgenden ein Beispiel zur MPE-Inferenz:
Abbildung 3: MPE-Inferenz für die Klassenzugehörigkeit des Punkts (12, 12).
Zunächst werden die Werte [latex]X=12[/latex], [latex]Y=12[/latex] in den passenden Blattknoten eingesetzt und die Dichten entsprechend der geschätzten Verteilungen bestimmt. Diese werden dann bis zum Wurzelknoten nach oben propagiert. Anschließend wird dort aufgrund des Summenknotens geschaut, auf welchem Pfad die höchste Wahrscheinlichkeit erzielt wurde. Diesem Pfad wird gefolgt, bis man alle Zielvariablen besucht hat. An den entsprechenden Blattknoten lassen sich dann die Belegungen der Zielvariablen ablesen. In diesem Fall wurde die höchste Wahrscheinlichkeit im rechten sub-SPN erzielt und die Belegung für [latex]C[/latex] ist 1. Der Punkt (12, 12) gehört schließlich zur orangen Klasse 1.
Auf diese Weise lassen sich MPE-Inferenzen also mit lediglich zwei Durchläufen durch die Graph-Struktur berechnen.
Fazit
In diesem Beitrag haben wir Sum-Product Networks vorgestellt, eine relativ junge Modellklasse im Maschinellen Lernen, die mit ihrer klaren Semantik, effizienten Inferenz und vielseitigen Anwendbarkeit eine gute Erweiterung zu bereits bestehenden Verfahren bildet. Für alle, die sich näher mit Themen rund um SPNs beschäftigen möchten, empfehlen wir zum einen die Originalarbeit von Poon und Domingos, sowie das Übersichtspapier von Paris.
