Erklärbare KI (englisch: Explainable AI, kurz XAI) ist zu einem wichtigen Aspekt bei der Entwicklung und dem Einsatz von Systemen der Künstlichen Intelligenz geworden. Da KI in unserem täglichen Leben eine immer größere Rolle spielt, ist es zunehmend wichtig zu verstehen, wie diese Systeme Entscheidungen treffen und welche Faktoren ihre Ergebnisse beeinflussen. Dies wird mit dem Aufkommen neuer Technologien wie Quantum Machine Learning (QML) noch dringlicher. Die XAI-Forschung geht auf diesen Bedarf ein, indem sie KI-Systeme entwickelt, die deren Funktionsweise erklären und Einblicke in die von ihnen getroffenen Entscheidungen geben können, oder indem sie für bestehende Systeme versucht, ihr Verhalten im Nachhinein zu erklären (Post-hoc-Erklärung). Dies trägt nicht nur dazu bei, Vertrauen in die Technologie aufzubauen, sondern ermöglicht es uns auch, potenzielle Verzerrungen zu erkennen und Anpassungen vorzunehmen, um die Genauigkeit und Fairness von KI-Systemen zu verbessern. Darüber hinaus ist die Fähigkeit, KI-Entscheidungen zu verstehen und zu interpretieren, von entscheidender Bedeutung. Denn nur so können wir sicherstellen, dass diese Systeme mit ethischen und rechtlichen Standards in Einklang stehen. Indem wir XAI einen hohen Stellenwert einräumen, können wir gewährleisten, dass sich KI auf eine verantwortungsvolle und transparente Weise entwickelt, die der Gesellschaft als Ganzes zugutekommt.
Shapley-Werte in XAI
Eine Methode aus dem Forschungsfeld der XAI sind die Shapley-Werte: Sie wurden von Lloyd Shapley in den 1950er Jahren entwickelt und sind ein mathematisches Konzept aus der kooperativen Spieltheorie. Im Kontext der Spieltheorie bieten Shapley-Werte eine Möglichkeit, den Gesamtwert eines kooperativen Spiels auf faire und ausgewogene Weise auf die Spieler zu verteilen. Die Idee besteht darin, jedem Spieler einen Anteil am Gesamtwert zuzuweisen, der proportional zu seinem Beitrag zum Spiel ist.
In den letzten Jahren wurden Shapley-Werte im Bereich des Maschinellen Lernens und der Künstlichen Intelligenz eingesetzt. Hier werden sie unter anderem verwendet, um die Wichtigkeit einzelner Merkmale (Feature) eines Datenpunktes zur resultierenden Vorhersage eines Modells in Zahlen auszudrücken. Dies ist vor allem für komplexe Modelle, wie zum Beispiel tiefe neuronale Netze, von Bedeutung, die schwer zu interpretieren sind. Nehmen wir an, wir haben die Möglichkeit, die Qualität der Ergebnisse eines KI-Systems zu messen, zum Beispiel in Form einer Punktzahl. Dabei kann es sich um die Vorhersagegenauigkeit, die Ausführungszeit, den Energieverbrauch oder eine beliebige andere Größe handeln, für die wir uns interessieren. Nehmen wir nun an, dass unser System als eine Anordnung von N Teilen (oder Akteuren) beschrieben werden kann, die wir einfach von 1 bis N aufzählen. Diese Teile könnten Neuronen in einem künstlichen neuronalen Netz, Merkmale im Eingabedatensatz oder einzelne Modelle in einem Ensemble sein. Eine Funktion, die jeder Kombination von Teilen eine Punktzahl zuweist, wird als Wertfunktion bezeichnet. Durch die Berechnung der Shapley-Werte lässt sich der durchschnittliche Beitrag der einzelnen Teile zum Gesamtwert ermitteln. Auf diese Weise können wir ihre Bedeutung innerhalb des Gesamtsystems bewerten. Mit diesem Wissen werden Modelle transparenter, da wir die Teile identifizieren können, die für die Entscheidung des Modells verantwortlich sind.
Anwendung von Shapley-Werten auf das Quantencomputing
Bisher war es eine weitgehend offene Frage, wie sich Shapley-Werte verhalten, wenn die Wertfunktion nicht deterministisch ist. Mit anderen Worten, sind Shapley-Werte immer noch zuverlässig, wenn sich die Eigenschaften des ML-Systems im Laufe der Zeit ändern, nur geschätzt werden können oder einer anderen Art von Ungewissheit unterliegen? In ihrer jüngsten Arbeit haben sich Wissenschaftler*innen der XAI-Gruppe des Lamarr-Instituts mit der Quantencomputing-Gruppe und Forscher*innen des Fraunhofer ITWM zusammengetan, um einen theoretischen Rahmen zu entwickeln, der die Bewertung von Shapley-Werten mit solchen unsicheren Wertfunktionen ermöglicht. Dazu modellieren sie die Wertfunktion als Zufallsvariable und analysieren die Auswirkungen auf die Verteilung der Shapley-Werte.
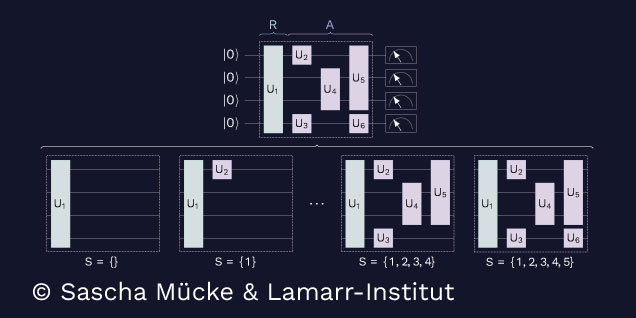
Beim klassischen Maschinellen Lernen werden Shapley-Werte meist zur Erklärung von Merkmalen der Eingabedaten verwendet. In ihrer jüngsten Arbeit wenden Forschende des Lamarr-Instituts und des Fraunhofer ITWM das Konzept an, um Gatter in einer Quantenschaltung zu erklären. Zu diesem Zweck nehmen die Gatter die Position von „Spielern“ in einem Koalitionsspiel ein, das für alle möglichen Kombinationen von Spielern ausgewertet wird, um den Beitrag jedes einzelnen Spielers zu bestimmen.
In einer Folgearbeit nutzten die Forscher*innen ihre theoretischen Erkenntnisse, um Shapley-Werte auf Quantencomputing anzuwenden. Ein Quantenschaltkreis ist das bekannteste Rechenmodell, das zur Durchführung von Quantenberechnungen verwendet wird. Es handelt sich um eine Reihe von Quantengattern, die den Quantenzustand eines Systems von Quantenbits (oder Qubits) manipulieren, um eine bestimmte Berechnung durchzuführen. Quantenschaltkreise können zur Durchführung einer Vielzahl von Algorithmen verwendet werden, darunter Quantensimulationen, Quantenoptimierung und Maschinelles Lernen mit Quanten (Quantum Machine Learning, QML). Quantencomputer können – zumindest theoretisch – bestimmte Probleme effizient lösen, die für klassische Computer als unlösbar gelten, wie zum Beispiel das Faktorisieren großer Zahlen und die Lösung bestimmter Suchprobleme.
Ein Blick ins Innere von Quantenschaltkreisen
In einem Quantenschaltkreis werden die Qubits in einem bekannten Zustand initialisiert, und dann wird eine Reihe von Quantengattern auf die Qubits angewandt, um ihren Zustand auf eine Weise zu verändern, die der gewünschten Berechnung entspricht. Der Endzustand der Qubits kodiert die Lösung des zu lösenden Problems. Die Messung des Endzustands bietet eine Möglichkeit, die Lösung zu extrahieren, aber diese Messung lässt den Quantenzustand kollabieren. Dies zerstört jegliche verbleibende Quantenkohärenz. Das Messergebnis ist probabilistisch, das heißt anstelle eines einzigen Ergebnisses kann bei jeder Messung des Quantenzustands eine Vielzahl von Ergebnissen mit einer bestimmten Wahrscheinlichkeit beobachtet werden. Man kann sich das so vorstellen, als würde man einen Würfel werfen, wobei der Würfel selbst dem Quantenzustand und dem Messergebnis des Wurfs entspricht: Auch wenn der Würfel selbst immer gleich ist, ist das Ergebnis dieser „Messung“, also der Würfelwurf, nicht deterministisch. Aus diesem Grund ist jede Eigenschaft, die wir aus der Messung eines Quantenzustands ableiten können, von Natur aus unsicher.
Die einzelnen Gatter kann man sich als Spieler in einem kooperativen Spiel vorstellen, von denen jedes zum Gesamtverhalten des Schaltkreises beiträgt. Durch die Berechnung der Shapley-Werte für jedes Gatter oder jede Gruppe von Gattern ist es möglich, den Beitrag jedes Gatters zum Endergebnis der Schaltung zu bestimmen und so das Verhalten des Quantensystems zu erklären.
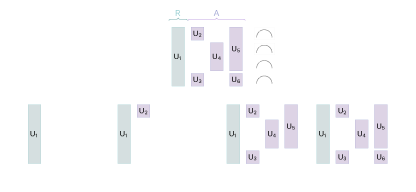
Dieses Bild zeigt, wie eine Quantenschaltung (oben) modifiziert wird, um den Beitrag der einzelnen Gatter zu bestimmen: Alle möglichen Teilmengen von Gattern werden separat bewertet, indem sie aus der Schaltung entfernt werden (unten) und die Auswirkungen auf die Wertfunktion beobachtet werden.
Diese Informationen können in einer Vielzahl von Zusammenhängen nützlich sein, zum Beispiel bei der Fehlersuche und Optimierung von Quantenschaltungen sowie bei der Verbesserung des Verständnisses von Quantensystemen durch Forscher*innen und Anwender*innen. Durch die Verwendung von Shapley-Werten zur Erklärung des Verhaltens einzelner Gatter ist es außerdem möglich, potenzielle Probleme zu erkennen und Anpassungen vorzunehmen, um die Genauigkeit und Robustheit von Quantenschaltungen zu verbessern. Darüber hinaus können unnötige Gatter entfernt werden, um die Schaltungstiefe zu verringern, die beim heutigen Quantencomputing ein wichtiger limitierender Faktor ist.
Wo sich XAI und Quantencomputing treffen
Die von den Forscher*innen verwendeten Wertfunktionen messen die Ausdrucksfähigkeit der Schaltungen (das heißt die Vielfalt der Funktionen, die sie realisieren können), die Verschränkungsfähigkeit (wie komplex der Quantenzustand werden kann) sowie die Klassifizierungsqualität in Quantum Machine Learning. Sie verwenden sowohl Simulatoren als auch reale Quantencomputer, um unsichere Shapley-Werte für eine Reihe verschiedener Schaltungen mit bis zu 20 Gattern zu berechnen. Ihre Ergebnisse deuten darauf hin, dass Shapley-Werte ein vielversprechender Weg sind, um die Rolle bestimmter Gatter in einem Quantenschaltkreis zu erklären. Jedoch sind aufgrund der inhärenten Unsicherheit von Quantencomputern viele Messungen erforderlich, um sie genau zu berechnen. Klassische Shapley-Werte erfordern bereits eine große Rechenleistung, und die probabilistische Natur der Quanteninformatik verschärft dieses Problem noch weiter. Daher sind weitere Forschungsarbeiten erforderlich, um diese Methode zu erweitern.
Insgesamt ist die Anwendung von Shapley-Werten auf Quantenschaltungen eine spannende Überschneidung von XAI- und Quantencomputer-Forschung, die das Potenzial hat, die Funktionsweise von Modellen für Maschinelles Lernen mit Quanten zu erhellen.
Mehr Informationen finden Sie in unseren Paper:
Shapley Values with Uncertain Value Functions
Heese, Raoul et al., 2023, arXiv preprint, pdf
Explaining Quantum Circuits with Shapley Values: Towards Explainable Quantum Machine Learning
Heese, Raoul et al., 2023, arXiv preprint, pdf
