
Zufallszahlen sind für viele Anwendungen im Bereich des Maschinellen Lernens (ML) essenziell. Sie werden für stochastische Optimierverfahren benötigt, außerdem um Datenpunkte aus den Verteilungen generativer Modelle zu ziehen, oder auch nur um die Parameter künstlicher neuronaler Netze zu initialisieren. Die Initialisierung solch eines Netzes bildet den Ausgangspunkt der Parameteroptimierung und hat einen großen Einfluss darauf, wie lang das Modell trainiert werden muss und wie leistungsfähig es danach ist. Eine verlässliche Quelle qualitativ hochwertiger zufälliger Zahlen ist daher ein wichtiges Werkzeug, und das nicht nur im Bereich der Künstlichen Intelligenz, sondern auch für viele andere Bereiche der Naturwissenschaften, zum Beispiel für Verschlüsselungsverfahren und Simulationen.
Was aber bedeutet hier „qualitativ hochwertig“? Intuitiv scheint Zufall gleich Zufall zu sein: Eine Reihe von Zahlen ist zufällig, wenn man nicht vorhersagen kann, welche Zahl als nächstes kommen wird. Allerdings kann man eine Vielzahl von Aussagen über alle bisher gesehenen Zahlen treffen und so Vermutungen anstellen, welche Eigenschaften die noch nicht beobachteten Zahlen besitzen. Wirft man eine Münze eine Million mal, so wird man beobachten, dass etwa 500.000 Würfe Kopf und etwa ebenso viele Zahl zeigen. Legt man Kopf=1 und Zahl=0 fest, so wird der Mittelwert aller Würfe bei ziemlich genau 0.5 liegen, und dieser Wert wird umso genauer je öfter man die Münze wirft. Beobachtet man hingegen, dass der Mittelwert konsistent bei 0.4 liegt – Zahl also deutlich häufiger als Kopf fällt – kann man davon ausgehen, dass die Münze manipuliert wurde, oder dass ein anderer Faktor das Ergebnis beeinflusst, etwa die Wurfhöhe oder die Ausgangsposition der Hand. Die Statistik bietet Methoden, um eine solche Abweichung von einer erwarteten Verteilung zu quantifizieren, beispielsweise durch Distanzmaße, wie der Kullback-Leibler-Divergenz oder der Hellinger- Distanz, oder aber durch statistische Tests, wie den Kolmogorov-Smirnov-Test.
Pseudozufallszahlen
Will man mithilfe eines Computers Zufallszahlen erzeugen, steht man vor einem Problem: Ein Computer ist eine deterministische Maschine, die feste Abfolgen von Befehlen ausführt. Es ist nicht möglich, mit solch einer Maschine echte Zufallszahlen zu generieren, da diese durch ein Programm erzeugt werden und so per Definition nicht zufällig sondern durch das Programm vorbestimmt sind. Um trotzdem Zahlen erzeugen zu können, die sich wie Zufallszahlen verhalten, enthalten Computer Programme, die mithilfe spezieller Algorithmen scheinbar zufällige Zahlen erzeugen – sogenannte Pseudozufallszahlen. Beginnend mit einer Zahl als Startzustand – auch „Seed“ genannt – werden diese „scheinbar“ zufälligen Zahlen durch Abfolgen arithmetischer sowie Bit-Operationen aus dem aktuellen inneren Zustand abgeleitet. Obwohl sie aussehen wie echte Zufallszahlen und viele derer Eigenschaften besitzen, kann man sie mit dem Wissen über den Ausgangszustand des Programms deterministisch reproduzieren. Insbesondere erzeugen Generatoren von Pseudozufallszahlen nur eine endliche Folge unterschiedlicher Zahlen ehe der Startzustand wieder erreicht ist und sie beginnen, sich zu wiederholen. Die Länge der Pseudozufallsfolge, die ein Algorithmus erzeugt, bevor er sich wiederholt, ist ein wichtiges Merkmal für seine Güte und wird „Periode“ genannt. Bekannte und häufig verwendete Algorithmen sind etwa Xorshift und Mersenne-Twister. Letzterer hat eine Periode von 219937 − 1, eine Zahl mit 6001 Stellen.
Quantenzufallszahlen
Quantencomputer stehen aktuell im Rampenlicht der Forschung. Die Ideen, wie man die Effekte der Quantenmechanik für das Maschinelle Lernen nutzen kann, sind kreativ und vielfältig. Während viele Forscher versuchen, komplette ML-Modelle über das Gatter-Modell in Quantencomputer einzubetten, suchen andere nach alternativen Ansätzen, um klassische ML-Verfahren durch Quanteneffekte zu verbessern.
Die zentrale Eigenschaft, die ein Qubit (also ein Quanten-Bit) von einem klassischen Bit unterscheidet, ist die Tatsache, dass ein Qubit nicht nur die Zustände 0 und 1 (die sogenannten Basiszustände), sondern unendlich viele Misch-Zustände annehmen kann. Solch ein Mischzustand |ψ〉 heißt Superposition und kann durch den Ausdruck |ψ〉 = α|0〉 + β |1〉 beschrieben werden. Dabei bezeichnen |0〉 und |1〉 die Basiszustände, und α und β sind komplexe Zahlen mit der Eigenschaft |α |² + |β |² = 1. Die sogenannte Bornsche Regel aus der Quantenmechanik besagt, dass ein Qubit mit Zustand |ψ〉 mit Wahrscheinlichkeit |α |² den Basiszustand 0 und mit Wahrscheinlichkeit |β |² = 1 − |α |² den Basiszustand 1 annimmt. Wir stellen also fest, dass sich die Messung eines Quantenzustandes sehr ähnlich zu einem Münzwurz verhält, nur dass die Wahrscheinlichkeit für Kopf oder Zahl über die Parameter α und β variabel ist. Setzen wir α = β = 1/√2, dann entspricht der Quantenzustand genau einem fairen Münzwurf, und wir beobachten beide Basiszustände jeweils mit Wahrscheinlichkeit 50%. Dieser Zustand, der auch als |+〉 bezeichnet wird, ist im Gatter-Modell des Quantencomputings besonders einfach herzustellen, denn er entsteht durch Anwenden des Hadamard-Gatters H – eines der grundlegendsten Gatter – auf ein Qubit im Basiszustand |0|.
Bringt man wiederholt ein Qubit in diesen Zustand und misst es, erhält man eine Reihe binärer Zufallszahlen, also eine Folge wie 10011100110111010110. . . Da diese Zahlen durch quantenmechanische Effekte erzeugt wurden, die mithilfe der klassischen Physik nicht erklärbar sind und nicht simuliert werden können, kann man sie als Zufallsquelle für die oben genannten Anwendungen benutzen und damit beispielsweise neuronale Netze initialisieren. Die Hoffnung, die Wissenschaftler*innen dabei hegen, ist, dass durch die hohe Qualität der Zufallszahlen maschinelle Lernmodelle besser initialisiert und somit schneller und zu einer höheren Güte trainiert werden können.
Quantenzufall in der Praxis
Diese Hoffnung schien sich kürzlich zu bewahrheiten, als Forschende aus Birmingham Quanten-Zufallszahlen zur Initialisierung mehrerer Modelle verwendeten, unter anderem neuronale Faltungsnetze. Dabei beobachteten sie, dass die Modelle, verglichen mit einer Initialisierung mit Pseudozufallszahlen, eine etwas höhere Trefferquote auf verschiedenen Klassifikationsdatensätzen erreichten.
Obwohl Quantencomputer auf Hochtouren erforscht und weiterentwickelt werden, bilden heutige Geräte das zuvor beschriebene mathematische Quantencomputing-Modell bei weitem nicht perfekt ab. Qubits werden mithilfe verschiedener physikalischer Mechanismen dargestellt, zum Beispiel mittels Mikrowellenstrahlung, durch supraleitende Materialien oder auch Photonen. Dabei gibt es viele Fehlerquellen, die das Ergebnis verzerren können [Abb. 1]. Im Rahmen ihrer aktueller Forschung haben Wissenschaftler*innen des ML2R untersucht, ob sich die Ergebnisse aus Birmingham reproduzieren und statistisch belegen lassen. Zu diesem Zweck nutzten sie einen Quantencomputer von IBM, um durch Anwenden des Hadamard-Gatters und Messen vieler Qubits eine große Menge von Quantenzufallszahlen zwischen 0 und 1 zu erzeugen.
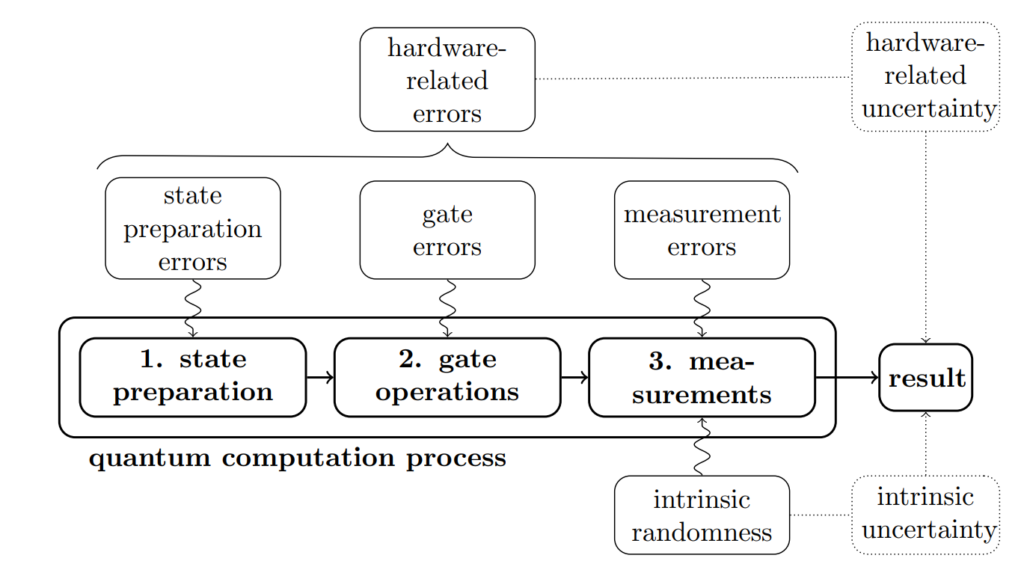
Verschiedene Quellen von Fehlern, die das erwartete Ergebnis eines Experiments auf einem Quantencomputer verzerren oder verfälschen können.
Sie stellten fest, dass die so erzeugten Zahlen nicht komplett zufällig sind, sondern vielmehr einer speziellen Verteilung folgen, die in [Abb. 2] dargestellt ist. Offensichtlich gibt es Zahlen, die deutlich häufiger auftreten als andere, was gegen eine Gleichverteilung spricht, die man bei komplett zufälligen Zahlen erwarten würde. Diese Verteilung entsteht, wenn jedes Bit nicht mit einer Wahrscheinlichkeit von 50% den Wert 1 hat, sondern etwas weniger: Gemessen wurde eine durchschnittliche Wahrscheinlichkeit von 48,88%. Es stellt sich also heraus, dass Quantenzufallszahlen – zumindest, wenn man sie naiv nach dem idealen mathematischen Modell erzeugt – deutlich weniger zufällig sind als solche, die Preudozufallszahlengeneratoren generieren.
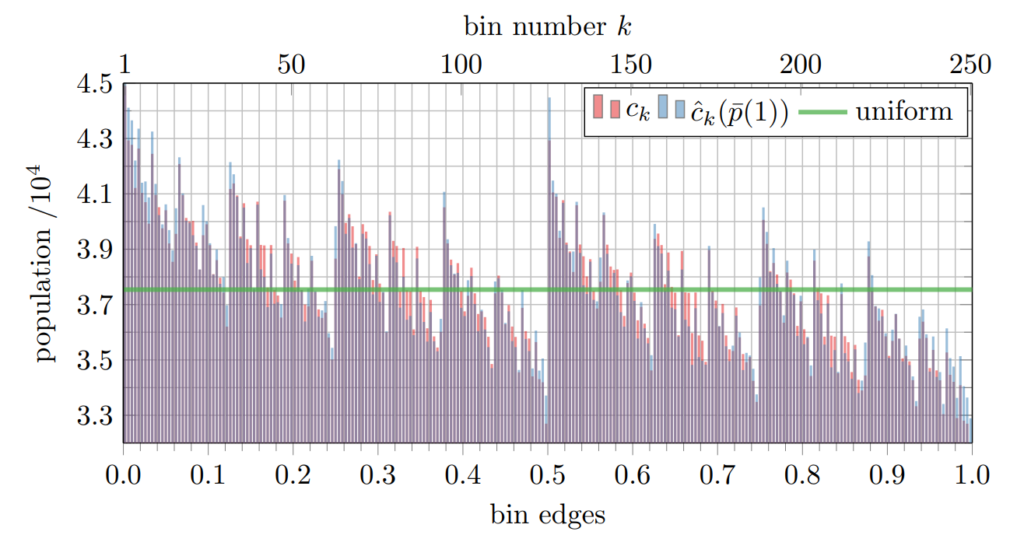
Beobachtete Verteilung der Zufallszahlen, die auf einem Quantencomputer von IBM erzeugt wurden (rote Balken). Die grüne Linie zeigt eine Gleichverteilung, wie man sie bei perfekten Zufallszahlen erwarten würde. Die blauen Balken zeigen eine durch Pseudozufallszahlen generierte Simulation der verzerrten Quantenzufallszahlen.
Neben diesen selbst generierten Zufallszahlen verwendeten die Forschenden weiterhin öffentlich verfügbare Zufallszahlen, die aus einem optischen Quantencomputer generiert wurden und qualitativ deutlich besser sind. Sowohl mit diesen als auch mit den selbst erzeugten Quantenzufallszahlen konnte im direkten Vergleich zu Pseudozufallszahlen kein signifikanter Effekt beim Trainieren von ML-Modellen beobachtet werden. Damit konnten die Forschenden zeigen, dass – zumindest bei den verwendeten Modellklassen – eine Quantenzufallsquelle nicht zu der beobachteten besseren Performance beim Lernen führt.
Fazit
Mögliche Anwendungen von Quanteneffekten für das Maschinelle Lernen sind vielfältig. Durch ihr inhärent stochastisches Verhalten können Qubits als Quelle von (echten) Zufallszahlen verwendet werden. Eine anfängliche Hoffnung, dass diese Zahlen zu besseren Ergebnissen beim Trainieren von ML-Modellen führt, wurde widerlegt. Dies liegt vermutlich einerseits an der hohen Güte moderner Generatoren von Pseudozufallszahlen, und andererseits an den technischen Hürden des Quantencomputings, die nur eine verzerrte Realisierung der in der Theorie perfekt zufälligen Zahlen zulassen.
Es gibt dennoch Hoffnung, dass uns auch diese verzerrten Verteilungen zu neuen Erkenntnissen verhelfen könnten: Sollte sich herausstellen, dass die Initialisierung bestimmter Modellklassen mit speziellen Verteilungen tatsächlich zu einer weitaus besseren Leistung führt, könnte dies genutzt werden, um solche Verteilungen auch mithilfe von Pseudozufallszahlen nachzubilden. Dass dies im Prinzip funktioniert, konnten die Forschenden des ML2R bereits zeigen, indem sie die Verteilung aus [Abb. 2] ganz ohne Quanten-Computing simulierten. Solange allerdings Quantencomputer noch so fehlerbehaftet in Bezug auf die Qualität ihrer Ausgaben sind wie heute, kann man nicht argumentieren, dass die „echte physikalische Zufälligkeit“ der Qubits allein eine messbare Auswirkung hat. Die Suche nach dem Durchbruch des Quantencomputings im Maschinellen Lernen geht also weiter.
Mehr Informationen im zugehörigen Paper:
On the effects of biased quantum random numbers on the initialization of artificial neural networks
Raoul Heese, Moritz Wolter, Sascha Mücke, Lukas Franken, Nico Piatkowski, 2021, PDF
