Als eine Form von Computer-Vision-Daten werden Punktwolken aufgrund ihrer ausgezeichneten Darstellung von 3D-Szenen häufig für die Navigation und die Lokalisierung von selbstfahrenden Autos und Robotern verwendet. In diesen Bereichen ist Sicherheit und Zuverlässigkeit von höchster Bedeutung: Durch KI-Manipulation verursachte Unfälle müssen so gut wie möglich verhindert werden. Herausfordernd bleiben bislang jedoch sowohl die Diagnose von Modellen durch KI-Fachleute als auch für die Vertrauenswürdigkeit der maschinellen Entscheidungsfindung für Nutzer*innen. Die meisten Machine-Learning-Modelle sind nicht transparent genug, um zurückverfolgen zu können, auf welcher Grundlage die Künstliche Intelligenz Entscheidungen trifft. Auch die Anpassung des Modells an Fehlerursachen ist eine große Herausforderung. Die Erforschung der Vertrauenswürdigkeit von Punktwolkenmodellen, das heißt von ihrer Erklärbarkeit, ist folglich von großer Relevanz. Leider wurde die Erklärbarkeit von Modellen, die Punktwolken im Vergleich zu Bildern verarbeiten, bislang nur wenig untersucht. Das Ziel unserer Arbeit ist es daher, eine bestehende Erklärbarkeitsmethode – LIME – an Punktwolken anzupassen und die Zuverlässigkeit der generierten Erklärungen durch die Eigenschaften von Punktwolkennetzwerken zu verbessern.
Tiefe neuronale Netze für Punktwolken
So wie sich Bilder aus Pixeln zusammensetzen, konstituieren einzelne Punkte die grundlegende Einheit von Punktwolken. In der Regel enthält ein Punkt zwei Arten von Informationen in sechs Dimensionen: Die ersten drei Dimensionen sind räumliche Koordinaten, die die Position an der X-, Y- und Z-Achse darstellen, und die letzten drei Dimensionen enthalten Informationen über den Farbwert, der als herkömmlicher RGB-Wert ausgedrückt wird. Anders als bei Bildern wird die Position eines Punktes durch die Koordinaten und nicht implizit durch den Index des Bildes dargestellt. Hierbei entsteht das Problem der Unordnung, da sich die physische Nähe der Punkte in der Punktwolkeninstanz unabhängig von der Reihenfolge verhält, in der sie in den Daten angeordnet sind. Dies verstößt gegen die Funktionsweise von Faltungsmatrizen, weshalb herkömmliche Convolutional Neural Networks (CNNs) nicht anwendbar sind. Glücklicherweise wurden in den letzten Jahren neue neuronale Netze für Punktwolken entwickelt, deren Leistungsfähigkeit mittlerweile zufriedenstellend ist.
Erklärbarkeitsmethoden
Aufgrund von Sicherheitsbedenken im Hinblick auf KI-Anwendungen hat sich die Erklärbarkeit von maschinellen Lernmodellen zu einem aufstrebenden Forschungsgebiet entwickelt (entsprechende Auseinandersetzungen finden Sie hier: Warum KI erklärbar sein muss). Erklärbarkeit kann in Abhängigkeit des Erklärungsobjektes grob in globale und lokale Methoden unterteilt werden. Globale Erklärungen sollen Nutzer*innen einen Überblick, zum Beispiel über die allgemeinen Entscheidungsgrundlagen des Modells, oder die allgemeine Datenverteilung verschaffen. Lokale Erklärungen dienen der Bereitstellung von Entscheidungsgrundlagen für einzelne Instanzen.
Die beliebten lokalen Erklärbarkeitsmethoden umfassen zwei Kategorien: gradientenbasiert und störungsbasiert. Gradientenbasierte Ansätze erfordern den Zugriff auf die internen Strukturen eines Machine-Learning-Modells und sind auch bekannt als White-Box-Test – Beispiele sind Layer-Wise Relevance Propagation (LRP), Taylor Decomposition und Integrated Gradients. Die störungsbasierten Ansätze erfassen lediglich die Beziehungen zwischen den In- und Outputs, um auf Merkmalsbedeutungen zu schließen. Sie werden daher auch als Black-Box-Test bezeichnet – Beispiele hierfür sind KernelShap und LIME.
Nachfolgend konzentrieren wir uns auf LIME (Local Interpretable Model-agnostic Explanations), eine leistungsfähige Erklärbarkeitsmethode, die theoretisch jedes Black-Box-Modell erklären kann. Ist eine Instanz gegeben, so wählt LIME zunächst eine große Anzahl von Mutationen in der Umgebung durch Perturbation (Störung) aus. Anschließend werden diese Mutationen in das Modell eingespeist, um Labels zu erhalten. Unter Verwendung der Mutationen und ihrer Labels wird ein simples und interpretierbares lineares Ersatzmodell trainiert, das die Entscheidungen des zu erklärenden Modells in der Nähe der gegebenen Instanz so genau wie möglich nachahmt. Schließlich kann durch eine Beobachtung der Gewichte des linearen Ersatzmodells die Bedeutung der Merkmale für die Vorhersage des ursprünglichen Modells abgeleitet werden.
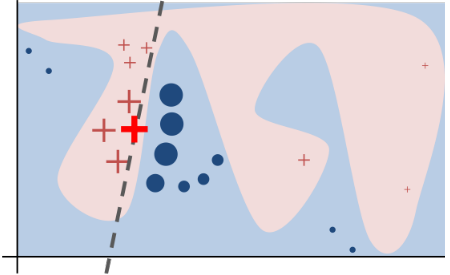
Graphische Darstellung der LIME Methode: Positive und negative Beispiele (X und O) werden um die zu erklärende Instanz herum ausgewählt (das hervorgehobene X). Anschließend werden diese Beispiele genutzt, um ein lokal erklärbares Ersatzmodell zu trainieren (die gestrichelte Linie).
LIME für Punktwolken
Obwohl LIME jedes Modell erklärt, kann die Plausibilität der Erklärungen noch weiter verbessert werden, wenn man die Eigenschaften des Punktwolkennetzes strategisch ausnutzt. In unserer Arbeit integrieren wir hierfür vornehmlich zwei Verfahren, um die Leistung des Ersatzmodells zu erhöhen: Farthest Points Sampling und Variable Input Size Flipping.

Eine Demonstration der Input-Instanz und ihrer vier Erklärungen mit unterschiedlichen Größen von Superpunkten: Die roten und blauen Anteile stellen positive beziehungsweise negative Zuordnungen zur Klassifikation dar.
Farthest Points Sampling (FPS)
Bei Bildern würde die Behandlung jedes einzelnen Pixels als Input Merkmal die Berechnungskomplexität stark erhöhen. Dies ist in der Praxis jedoch kaum umsetzbar. Denn insbesondere bei hochauflösenden Bildern ist eine sehr hohe Verarbeitungszeit für Nutzer*innen inakzeptabel. Die bislang bestehende Lösung hierfür sieht vor, die gebündelten Superpixel als ein Merkmal zu behandeln. Dies wirft jedoch die Frage auf: Wie kann man Superpunkte rationaler gruppieren?
In Bildern ermöglicht eine semantische Segmentierung geeignete Superpixel zu erhalten. Dies ist aber leider nicht auf Punktwolken anwendbar. Die intuitivste Antwort ist eine zufällige Segmentierung. Wenn die Segmentierung jedoch nicht einheitlich ist, konzentrieren sich die wichtigsten Zuschreibungen auf große Superpunkte. Diese Erklärung ist für den Erklärenden jedoch nicht von Nutzen, da der menschliche Verstand Segmenten mit mehr Punkten eine größere Bedeutung beimisst. Um dieses Problem zu adressieren, haben wir den K-Mean-Clustering-Algorithmus mit FPS eingeführt. Bei dieser Methode wird willkürlich ein Startpunkt ausgewählt. Anschließend wird der Punkt, der am weitesten von dem K-Punkt entfernt liegt, als K+1er abgetastet. Diese einfache und intuitive Methode erzwingt, dass die anfänglichen Zentren im K-Mean-Clustering gleichmäßig auf der Instanz-Oberfläche verteilt werden. Experimentell hat sich gezeigt, dass dieses Modul die Plausibilität der Erklärungen verbessert.
Variable Input Size Flipping (VISF)
Bei der Perturbation von Bildern steht man oft vor einer schwierigen Wahl: Was genau ist der Substitutionswert für die Störung? In bestehenden Studien wurden verschiedene Lösungen angeführt, zum Beispiel Nullwerte, zufällig gewählte Zahlen oder der Durchschnitt der Instanzen. Diese scheinen intuitiv möglich zu sein, haben aber keine strikte theoretische Grundlage. Eine intuitive Wahl kann zudem die Plausibilität der Erklärung gravierend beeinflussen. Wir überwinden dieses Problem, indem wir die strukturellen Eigenschaften von Punktwolkennetzen nutzen. Da Punktwolken nicht indexiert sind, haben die Netze keine Anforderung an die Größe des Inputs. Daher ist das Entfernen von Punkten, die gestört werden müssen, direkt aus der Input-Punktwolke eine alternative Lösung ohne Rücksicht auf Informationsreste nehmen zu müssen.
Quantitative Evaluationen
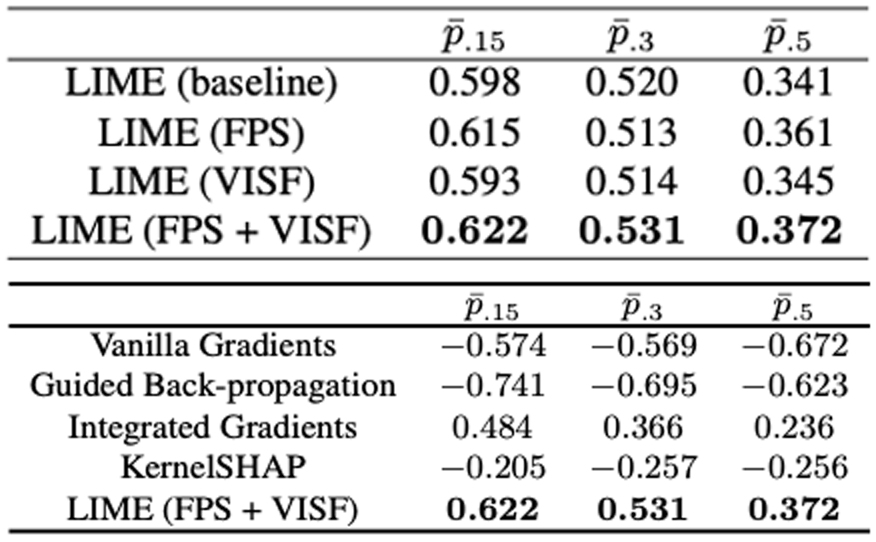
Zwei quantitative Metriken werden in unserer Arbeit für ersatzmodellbasierte Erklärbarkeitsansätze herangezogen: lokale Treue und Plausibilität. Die lokale Treue bewertet die Verhaltensähnlichkeit des Ersatzmodells mit dem zu erklärenden Modell. Sie ist einfach zu ermitteln und ergibt sich aus der Differenz zwischen den Vorhersagewerten des Ersatzmodells und des zu erklärenden Modells auf dem gestörten Trainingsdatensatz. Plausibilität untersucht die Genauigkeit der generierten Erklärung für die Vorhersage und ist eher schwer zu bestimmen, da die Ground-Truth-Erklärung nicht verfügbar ist. Der Ablationstest ist in diesem Kontext eine intuitive Option: Eine Erklärung wird dann als zuverlässig erachtet, wenn das Vertrauen des Modells in seine Vorhersage signifikant abfällt, nachdem jener Teil mit der größten Zuschreibung innerhalb der Erklärung gestört wurde. In ähnlicher Weise führten wir VISF auch in den Ablationstest der Punktwolke ein, um diesen genauer zu gestalten, ohne uns um die verbleibenden Informationen in den abgetragenen Beispielen zu kümmern.
Toolkit: Erklärung von Punktwolkennetzen
Unser Toolkit mit agentenbasierten interpretierbaren Methoden für Punktwolken ist auf Github verfügbar: https://github.com/Explain3D/LIME-3D
Das gesamte Projekt wurde auf PyTorch aufgebaut und auf Python 3.6 mit PyTorch 1.7.0 getestet. Das Standardklassifizierungsmodell ist PointNet. Da der auf Ersatzmodellen basierende Erklärbarkeitsansatz jedoch modellunabhängig ist, kann es durch beliebige Alternativen ersetzt werden. Wir stellen auch die im Beitrag beschriebenen Bewertungstools zur Verfügung, und der gesamte Bewertungsprozess wird mit dem ModelNet40-Datenset durchgeführt.
Mehr in der zugehörigen Publikation:
Surrogate Model-Based Explainability Methods for Point Cloud NNs Hanxiao Tan, Helena Kotthaus. Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, 2022, PDF.
