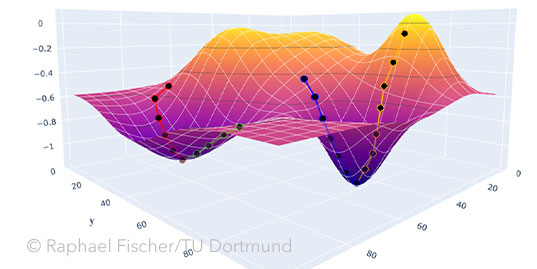
Optimierung ist ein zentraler Bestandteil des Maschinellen Lernens, die es ermöglicht, Modelle an Daten anzupassen und somit zu trainieren. Gleichzeitig sind der Begriff und die darunter fallenden Verfahren für viele Leute abstrakt und ungreifbar.
Bereits in der Schulmathematik wird Optimierung genutzt, um Minima und Maxima (Tief- und Hochpunkte) von Funktionen zu finden. Allgemein gilt es bei Optimierungsproblemen jene Kombinationen bestimmter einstellbarer Größen (Parameter) zu bestimmen, mit der das beste Ergebnis bezogen auf eine festgelegte Aufgabe erzielt werden kann. Solche Probleme treten in diversen Domänen auf:
- Wirtschaft: Zur Gewinnmaximierung muss die ideale Festlegung von Preisen, Arbeitsverteilung, Personal etc. gefunden werden.
- Logistik & Versand: Die Positionierung von Verteilzentren soll evaluiert werden, damit die durchschnittlich benötigte Lieferzeit minimiert werden kann.
- Physik: Das Energie-Minimum in einem physikalischen System soll untersucht werden.
- Klimaforschung: Statistische Klimamodelle müssen auf real gemessene Daten angepasst werden, welche komplexen hydrodynamischen Prozessen entspringen.
Es zeigt sich: Optimierung kommt in einer Vielzahl von Forschungsbereichen und Anwendungskontexten zum Einsatz. Im Maschinellen Lernen erlaubt sie, ein Modell und seine Parameter im Training an die vorliegenden Daten anzupassen (ähnlich wie beim oberen Klima Beispiel).
Wie gut ist das Modell? – Die Zielfunktion
Beim Maschinellen Lernen beeinflussen Parameter das Verhalten eines Modells. Mithilfe von Optimierung soll die optimale Belegung der Parameter gefunden werden. Hierfür werden Trainingsdaten mit Label genutzt, für die das Modell mit konkreten Parameterbelegungen Vorhersagen machen kann. Aus den vorhergesagten Labels und den bekannten, korrekten Trainingslabels lässt sich die Güte dieser Belegung abschätzen (durchschnittlicher Fehler). So ergeben sich mögliche Zielfunktionen für Optimierungsprobleme, zum Beispiel: Finde die Parameter und entsprechende Modellvorhersage, mit …
- … der geringsten (quadratischen) Abweichung (least squares)
- … der höchsten Plausibilität (likelihood)
Die Zielfunktion wird in der Anwendung auch auch oft als Verlust- (loss), Güte- oder Fitnessfunktion bezeichnet. Da intuitiv Verlust minimiert und Güte und Passgenauigkeit maximiert werden sollte, werden die entsprechenden Zielfunktionen meist invertiert (Minima sind dann Maxima). Bei einem niedrig dimensionalen Parameterraum lässt sich die Funktion auch grafisch darstellen. Die optimalen Lösungen entsprechen hierbei den Tiefpunkten beziehungsweise Tälern. Man unterscheidet zwischen lokalen Minima, die nur in einem gewissen Umfeld optimal sind, und globalen Minima, welche für den gesamten Parameterraum den niedrigsten Zielfunktionswert besitzen.
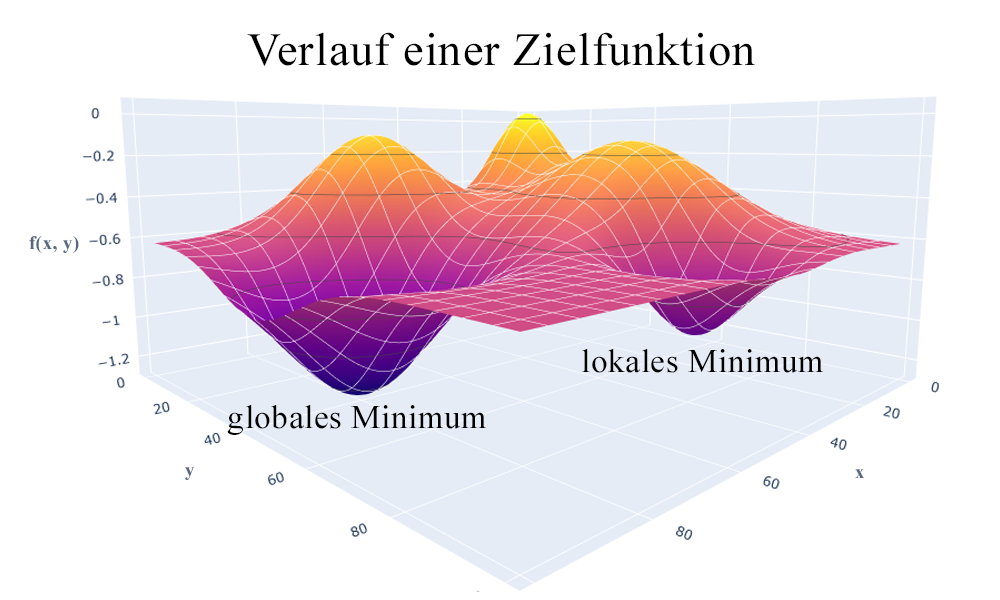
Zweidimensionaler Parameterraum x, y mit zugehörigen Zielfunktionswerten f(x, y), einem lokalen Minimum an x=40, y=80 sowie einem globalen Minimum bei x=80, y=40.
Lösen eines Optimierungsproblems
Je nach Art der Zielfunktion gibt es verschiedene Ansätze zum Lösen des Optimierungsproblems. Bei einigen Funktionen (kontinuierlich und differenzierbar) können Optima über die Ableitungen der Funktion (notwendiges und hinreichendes Kriterium für Gradienten erster und zweiter Ordnung) bestimmt werden. Bei einem großen Parameterraum lässt sich dieses Problem jedoch nicht mathematisch geschlossen lösen. Stattdessen können hier Gradientenabstiegsverfahren genutzt werden, bei denen man sich schrittweise dem Optimum annähert. Ausgehend von einer Startposition wird abwechselnd der Gradient mit den aktuellen Parametern berechnet, und eine Veränderung der Parameter in Richtung des Gradienten vorgenommen, bis keine Verbesserung mehr erzielt werden kann. Für viele Methoden (zum Beispiel künstliche Neuronale Netze) wird der aktuelle Gradient lediglich stochastisch (für einen Teil der Daten) geschätzt. Entsprechend sind weniger Vorhersagen und Gradientenberechnungen nötig. Dies beschleunigt die schrittweise Optimierung.
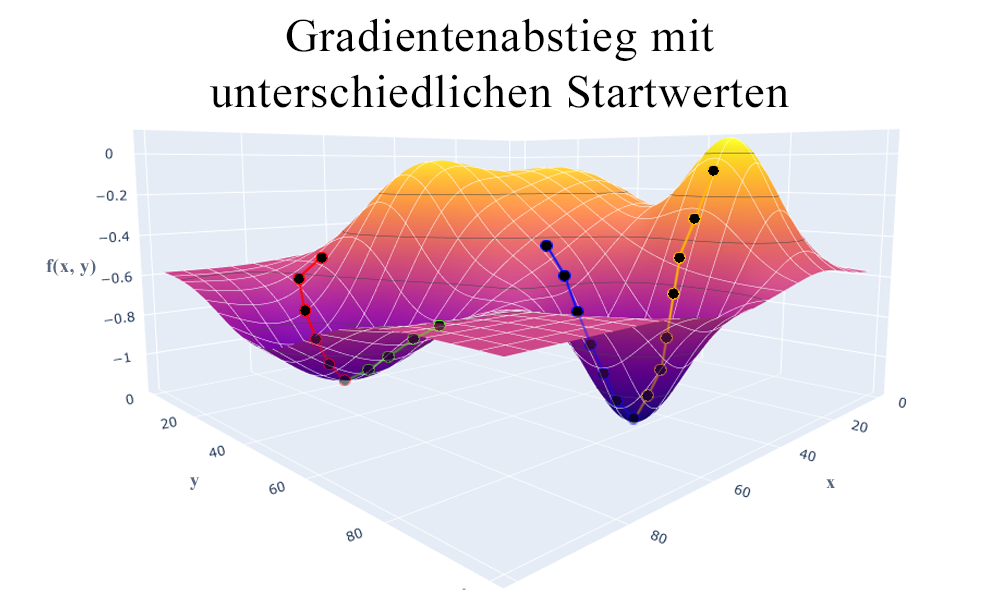
Ein Gradientenabstieg nähert sich schrittweise dem Minimum, basierend auf den berechneten oder stochastisch abgeschätzten Gradienten der aktuellen Position im Parameterraum. Je nach Wahl des Startpunktes werden jedoch gegebenenfalls nur lokale Minima erreicht, weswegen das Verfahren in der Praxis oft mehrfach gestartet und durchgeführt wird (hier exemplarisch mit vier Startwerten).
Lassen sich keine Gradienten bestimmen, so kann man versuchen den Parameterraum systematisch abzusuchen. Bekannte Vertreter dieser Idee sind das Intervallhalbierungs-, das goldener-Schnitt- und das Nelder-Mead-Verfahren. Sie unterteilen den Parameterraum iterativ und versuchen so, immer niedrigere Werte für die Zielfunktion zu finden.
Gradientenabstiegs- und Suchverfahren finden in der Regel jedoch nur lokale Minima, abhängig vom gewählten Startpunkt. Mit Hilfe von Multi-Start-Verfahren lassen sich parallel mehrere Optimierungen durchführen. So können mehrere lokale Optima gefunden werden, unter denen sich auch ein globales Optimum befinden kann. Eine ähnliche Idee verfolgen Evolutionäre Algorithmen, welche an die Evolutionstheorie angelehnt sind. Diese Verfahren verändern schrittweise (Generationen) eine Gruppe (Population) von Parameterbelegungen (Individuen). Über bestimmte Mutations- und Rekombinationsmethoden werden neue Belegungen erzeugt, von denen ein Teil (abhängig von ihrer Nützlichkeit) für die nächste Generation “überlebt”.
Optimierung als Schlüssel zum Ziel
Optimierung ist möglicherweise die wichtigste Schlüsselkomponente im Maschinellen Lernen, da sie den gesamten Lern- bzw. Trainingsprozess steuert. Die Teilschritte der Optimierung klingen zunächst komplex, werden jedoch in der Regel vollautomatisch von Computern bewältigt. So sind für die bekannteren Methoden des Maschinellen Lernens die zugehörigen Optimierungsverfahren bereits implementiert und verfügbar, sie werden lediglich über einige Stellschrauben/Hyperparameter (Schrittweite, Anzahl der Startpunkte etc.) konfiguriert. Ein tieferes Verständnis für die Optimierung ist jedoch unabdingbar, um auch bei schwieriger Datenlage oder einem besonders komplizierten Lernproblem gute Ergebnisse zu erreichen. In unserem vierten Beitrag der ML-Basics Reihe erklären wir, welche Tools für das Maschinelle Lernen in der Praxis relevant sind.
