Während klinischer Studien ist es unter anderem sehr wichtig die Wirksamkeit der Therapie zu beurteilen und ein Krankheitsmonitoring über den gesamten Zeitraum zu machen. Diese Beurteilungen können anhand der Bestimmung des Aktivitätsgrad der Krankheit (Stärke/ Ausprägung einer Krankheit) vorgenommen werden. Deshalb enthalten klinische Studien neben den objektiv gemessenen Werten, wie zum Beispiel Laborwerte, auch subjektive Experteneinschätzungen zur Bestimmung der aktuellen Aktivität der untersuchten Krankheit. Die Verfahren der Aktivitätseinschätzung unterscheiden sich je nach Krankheit. Dieser Beitrag spezialisiert sich auf die Einschätzung der Aktivität der Krankheit Psoriasis Arthritis (PsA), eine Schuppenflechte mit Gelenkbeteiligung.
Da die subjektiven Einschätzungen der Aktivität von PsA starken Schwankungen unterliegen, die durch unterschiedliches Expertenwissen und Intuition der Ärzt*innen bedingt werden, wird im Folgenden ein Verfahren vorgestellt, das eine robustere und stabilere Einschätzung des Patient*innen-Status vorhersagen soll.
Aktivitätseinschätzung von Patient*innen
Generell existieren zwei weitverbreitete medizinische Methoden, um den aktuellen Status der Krankheit zu bestimmen:
- Zum einen kann der Status anhand des numerischen Krankheitsaktivitätsrating von den Ärzt*innen bestimmt werden. Dieser Score erfordert Domänenexpertise und ist zudem sehr subjektiv, da keine strengen diagnostischen Kriterien festgelegt sind.
- Zum anderen kann der Krankheitsstatus anhand von bestehenden Symptomen berechnet werden. Diese Methode ist objektiver, erfordert jedoch ebenfalls Domänenwissen, um die einzelnen Attribute korrekt zu gewichten.
In einer Studie des Fraunhofer IAIS und ITMP wurde die Methode Ranking SVM weiterentwickelt, um aus den vorhandenen medizinischen Bewertungen der Krankheit eine robustere und stabilere Einschätzung der Aktivität von PsA vorherzusagen. Die Vorhersage besteht aus einer Kombination der zwei vorhandenen Einschätzungen. Im Folgenden wird die Methodik zur Lösung der Aktivitätsbestimmung beschrieben.
Wie ordnet eine Ranking SVM die Krankheitsaktivitäten?
Die beschriebene Herausforderung bei der Einschätzung von Krankheitsaktivitäten kann auf das Problem von ordinalen Regressionen zurückgeführt werden. Eine ordinale Regression ist eine Kombination aus einer reinen Klassifikation und einer Regression: Die Datenpunkte sind unterschiedlichen Klassen zugeordnet und es existiert eine lineare Ordnung zwischen den Klassen. Eine Ordnung zwischen Datenpunkten kann nicht nur zur Einordung von Aktivitäten von Krankheiten verwendet werden, sondern wird unter anderem auch in der Informationsgewinnung und in der Ökonometrie genutzt. Hierbei stellt die Ordnung meist eine Präferenz dar: Objekt A wird Objekt B vorgezogen (AB). Im Folgenden soll die Methode anhand des Beispiels von PsA-Patient*innen beschrieben werden.
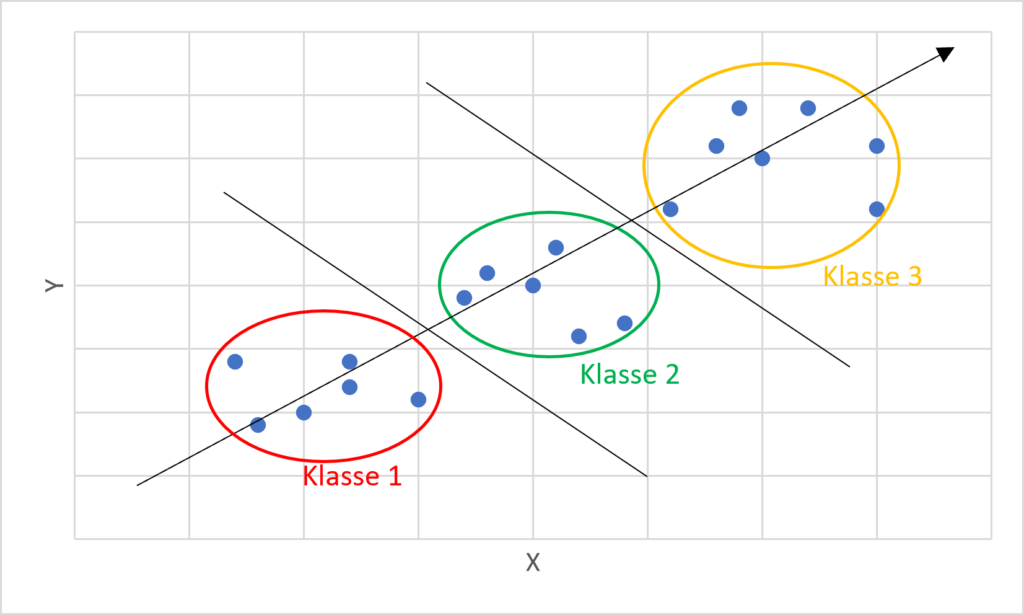
Beispiel einer ordinalen Regression. Klassen 1-3 werden durch parallele Hyperebenen getrennt.
Eine Möglichkeit ordinale Regressionen zu lösen bietet die Ranking Support Vector Machine (Ranking SVM). Die Ranking SVM lernt eine Ordnung zwischen den Krankheitsaktivitäten der Patient*innen. Das bedeutet, dass Patient*innen anhand der Stärke der Aktivität von PsA geordert werden. Das Label, nachdem sortiert werden soll, stellt die Einschätzung der Ärzte dar. Die Symptome sowie deren Gewichtung werden als Feature Vektor benutzt. Um den Einfluss der starken subjektiven Schwankungen der Aktivitätseinschätzungen zu verringern, werden nur Patient*innen-Paare für das Trainieren verwendet, die messbar unterschiedliche Symptome und Aktivitätsstatus haben.
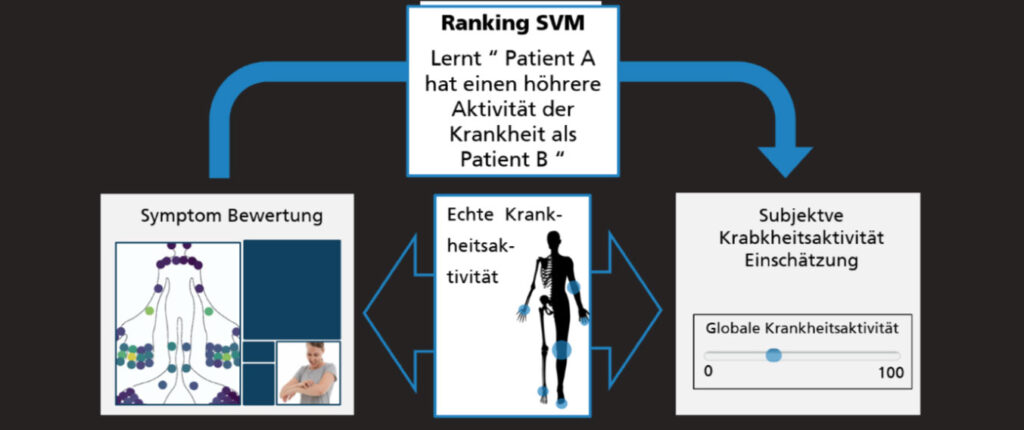
Beispiel einer ordinalen Regression. Klassen 1-3 werden durch parallele Hyperebenen getrennt.
Anhand des gelernten Gewichtsvektors kann ein neuer Aktivitätswert je Patient*in berechnet werden und die Aktivität der Krankheit gegenüber anderen Patienten eingeordnet werden. Die Umwandlung des ordinal skalierten Datensatzes in binären Klassifizierungsdatensatz ermöglicht eine ordinale Regression anhand einer Klassifizierungs-SVM.
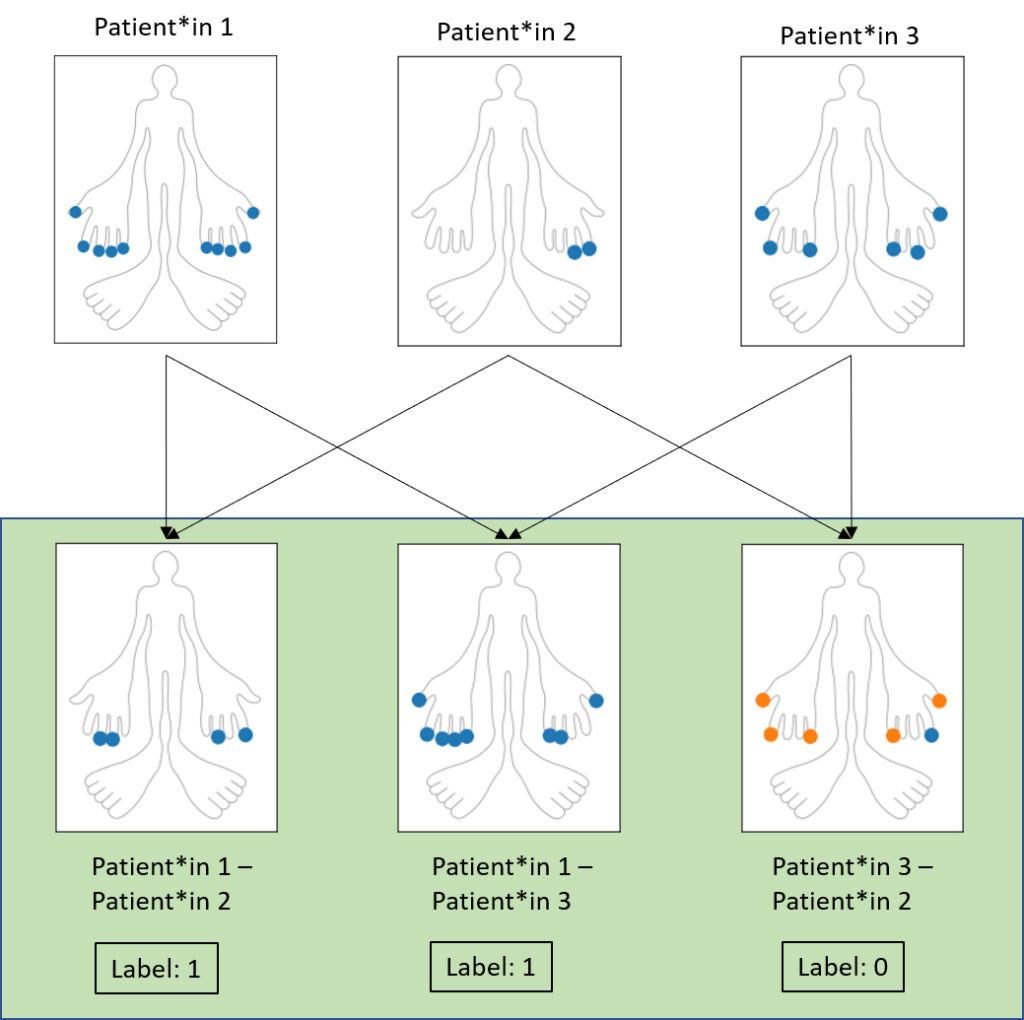
Ordinal skalierte Ordnung von Patient*innen (links höchste Krankheitsaktivität, recht geringste Krankheitsaktivität) und die Differenz zwischen den Patient*innenpaaren (blau- positiver Wert, orange- negativer Wert).
Während der Anpassung des Datensatzes werden die Datenpunkte (Patientinnen) paarweise betrachtet und die Differenz der Punkte berechnet. Durch die Differenz können zwei Punkte in eine Ordnung zueinander gebracht werden. Im Fall der PsA Patientinnen zeigt die Differenz an, ob bestimmte Symptome beim Minuenden stärker oder schwächer vertreten sind als beim Subtrahenden. Positive Werte bedeuten demnach, dass die Krankheit bei dem/ der ersten Patientinnen stärker vertreten ist; bei negativen Werten ist die Krankheit schwächer vertreten. Falls die Symptome bei Patientinnen gleich stark vertreten sind, heben diese sich während der Differenzbildung auf. Ist der Minuend in der Ordnung höher, so wird das Label der Differenz auf 1 gesetzt, ansonsten auf 0 (siehe obenstehende Grafik). Nun haben wir einen Datensatz, der für das Trainieren von binären Klassifizierungsmodellen, wie der SVM, verwendet werden kann.
Training der Klassifizierungs-SVM
Dieser modifizierte Datensatz kann nun verwendet werden, um eine SVM für binäre Klassifikationsprobleme zu trainieren. Hierbei wird die Ordnung von Objektpaaren anstatt von Klassen gelernt. Von der trainierten SVM kann eine Gewichtsvektor als auch eine Entscheidungsfunktion ermittelt werden. Durch Multiplikation der Datenpunkte mit dem gelernten Gewichtsvektor wird eine Approximation des Rangs der Krankheitsaktivität des Patienten berechnet. Neue Datenpunkte können so in die bestehende Ordnung einsortiert werden. Die detaillierte Methodik kann in dem Paper von Herbich et al. nachgelesen werden.
Am Ende liegt ein Modell vor, dass die Krankheitsaktivitäten von Patient*innen anhand von den Symptomen vorhersagen kann. Über diese Abschätzung der Krankheitsaktivitäten kann der Status eines Patienten über einen längeren Zeitraum verfolgt werden oder es können Patienten nach dem Schweregrad der Aktivität geordnet werden.
Um den Erfolg einer Therapie während einer klinischen Studie bewerten zu können, ist es wichtig, ein Aktivitätslevel der Krankheit zu bestimmen. Klinische Studien enthalten neben objektiv gemessenen Indikatoren der Patientinnen, wie Laborwerte, oftmals subjektive Experteneinschätzungen, wie die Krankheitsaktivität von Arthritis der Teilnehmerinnen. Diese Einschätzungen enthalten starke Schwankungen durch unterschiedliches Expertenwissen und Intuition der Ärztinnen. Wir haben gezeigt, dass dies über die Ranking SVM bestimmt werden kann. Durch das Modell werden die subjektiven Einflüsse der Mediziner verringert und genauere Abschätzungen des Zustandes der Patientinnen können vorgenommen werden. Dabei schneidet die Ranking SVM in unserer Studie mit einer Genauigkeit von 80% am besten ab.
Mehr Informationen in der zugehörigen Publikation:
Aligning Subjective Ratings in Clinical Decision Making A. Pick, S. Ginzel, S. Rüping, J. Sander, A. C. Foldenauer, M. Köhm, 2020, arXiv
