Wissensgraphen werden von vielen Organisationen genutzt, um relevante Informationen zu speichern und zu strukturieren. In Wissensgraphen werden Entitäten durch Knoten dargestellt und Beziehungen durch Kanten. In dieser Darstellung kann man beispielsweise sehen, dass Carl Gotthard Langhans der Architekt des Brandenburger Tors ist.
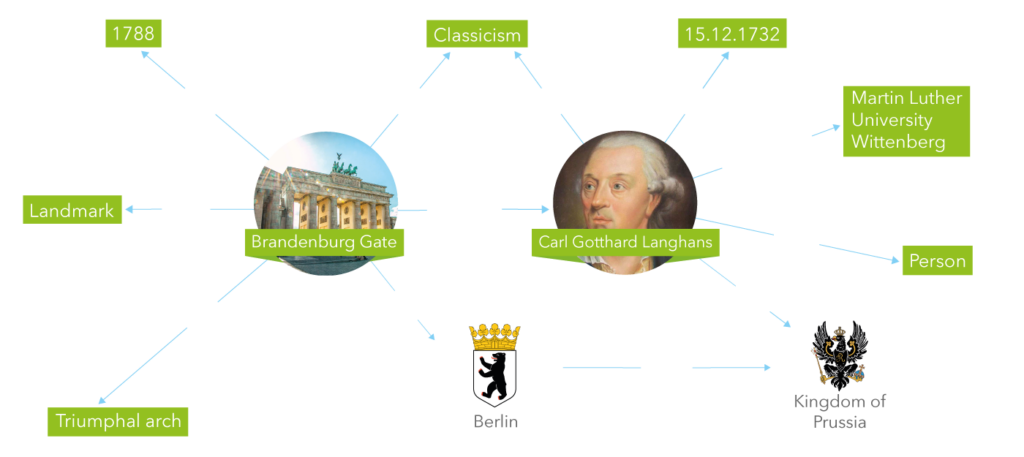
Abbildung 1: Muster Wissensgraph
Die meisten gegenwärtigen Methoden des maschinellen Lernens erfordern einen Input in Form von Features, das bedeutet, dass sie nicht direkt einen Graphen als Input nutzen können. Aufgrund dessen ist unser Ziel Merkmaldarstellungen, sogenannte Einbettungen, von Entitäten und Beziehungen in Wissensgraphen zu erlernen.
Einschränkungen vorhandener Einbettungsmodelle
Die Vorhersage von Zusammenhängen zwischen den Verbindungen mit der Verwendung von Knowledge Graphs Embedding (KGE) Modellen ist zu einer beliebten Vorgehensweise für die Vervollständigung von Wissensgraphen geworden. Solche Modelle setzen eine Transformationsfunktion ein, die Knoten über Kanten in einem Vektorraum abbildet, um die Wahrscheinlichkeit der Verknüpfung zu messen. Während der Abbildung der individuellen Knoten wird auch die Struktur des Teilgraphens transformiert. Die meisten bereits vorhandenen KGEs wurden in euklidischer Geometrie entworfen und unterstützen üblicherweise einen einzelnen Transformationstypen – häufig Übersetzung oder Rotation.
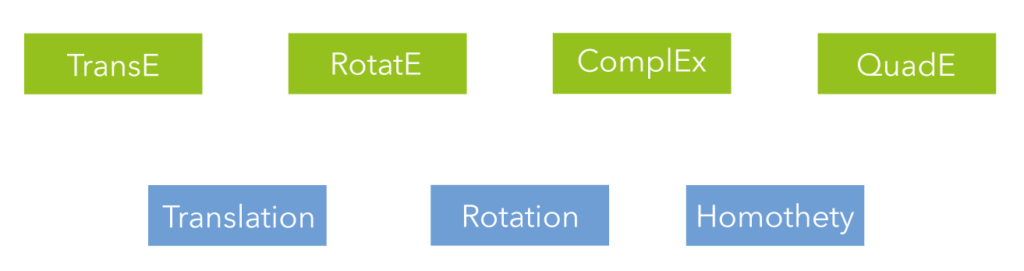
Abbildung 2: Transformationsfunktion von Einbettungsmodellen für Wissensgraphen
Dies schränkt die Fähigkeit von KGE-Modellen ein, Wissensgraphen mit komplexen Motiven in Teilgraphen einzubetten, insbesondere wenn mehrere Strukturen in der Nachbarschaft existieren. Ein Beispiel von solch einer Situation ist die Anwesenheit einer Pfadstruktur für eine Gruppe von Knoten in der Nähe einer Loop-Struktur, einer anderen Gruppe in einem Wissensgraphen (wie in der folgenden Abbildung dargestellt):

Abbildung 3: Beispiel einer Graph- und Vektordarstellung von Pfad/Loop
Projektive Transformationsfunktionen
Projektive Transformationen enthalten simultane Transformationen, die folgendes umfassen: Übersetzung, Rotation, Homothetie, Reflexion und Inversion und bilden die Grundlage unserer Vorgehensweise.
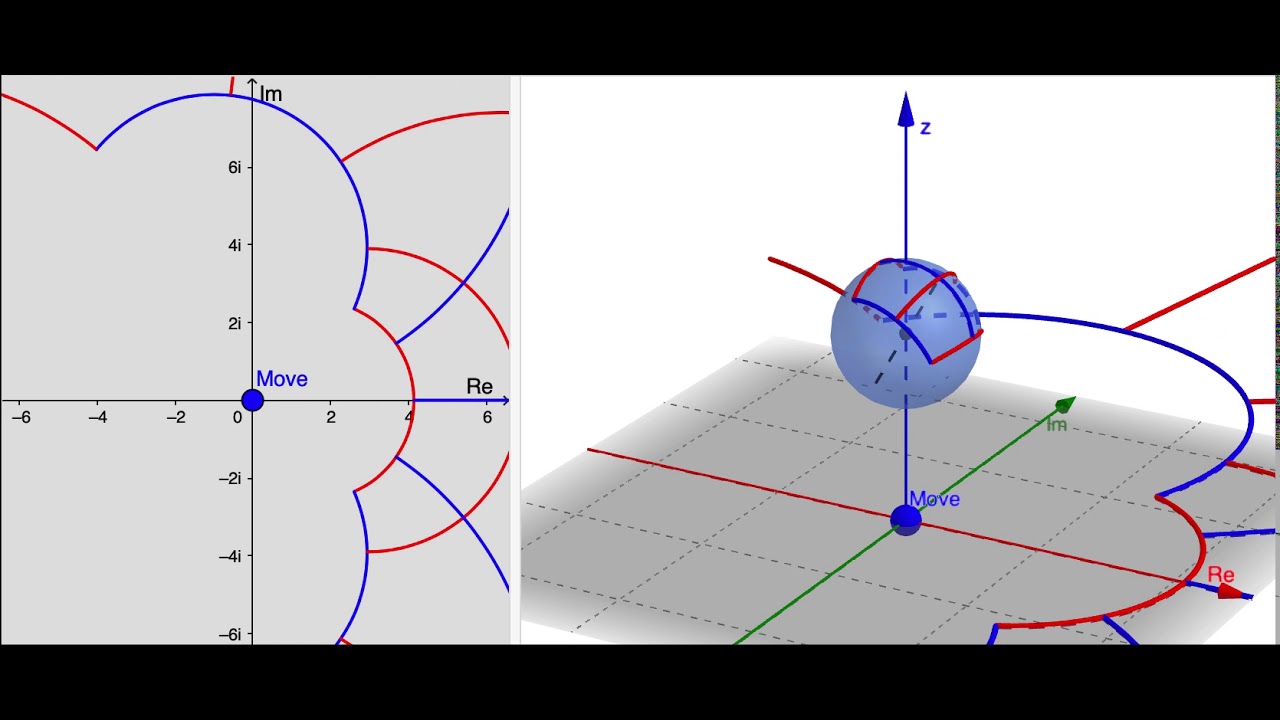
Wie man im Video sieht, liegt eine Kugel auf einer Ebene. Für jeden Punkt auf der Kugel (außer dem Nordpol) gibt es ein Gegenstück auf der komplexeren Ebene, das durch die Projektion von der Kugel auf die Ebene erhalten wird. Die Punkte, die näher am Nordpol liegen, werden auf eine größere Entfernung abgebildet und der Nordpol wird auf der Ebene bis ins Unendliche projiziert.
Hier bilden Sequenzen von Punkten (auf der Kugel oder der Ebene) Strömungen. Der Übergang von einem Punkt zu einem anderen Punkt erfolgt durch die projektive Transformation. Diese ist eine parametrische Funktion. Abhängig von den Werten der Parameter gibt die projektive Transformation dem Vektorraum (Form der Strömungen) verschiedene Formen, nämlich kreisförmig, elliptisch, hyperbolisch, parabolisch und loxodromisch.
Im Fall von kreisförmigen Vektorräumen hat die projektive Transformation einen Fixpunkt (hier ist der Fixpunkt im Ursprung). Die Strömungen sind kreisförmig um den Fixpunkt gestaltet. Im Fall der Ellipse hat die projektive Transformation zwei Fixpunkte und die Strömungen zirkulieren um jeden von ihnen. Bei hyperbolischen Formen gibt es auch zwei Fixpunkte, aber hier stammen die Strömungen aus einem Fixpunkt und sinken in einen anderen. Parabolische Vektorräume enthalten einen Fixpunkt (hier am Nordpol) und die Strömungen auf der Kugel beginnen an einem Punkt und kehren nach dem Passieren der Kugel wieder zum Fixpunkt zurück. Hier ist zu beachten, dass die Strömungen auf der Kugel zu geraden Linien auf der Ebene werden. Im Falle von loxodromischen Formen gibt es zwei Fixpunkte auf der Kugel (ein Fixpunkt ist nahe dem Nordpol auf der Kugel und der andere ist nahe dem Südpol). Die Strömungen stammen aus einem Fixpunkt und sinken spiralförmig in den anderen. Nach der Projektion der Strömungen von der Kugel auf die Ebene befindet sich ein Fixpunkt in der Nähe des Ursprungs auf der Ebene und der andere wird in größerer Entfernung projiziert. Daher durchlaufen die Strömungen auf der Ebene von einem Fixpunkt zum anderen eine große Distanz auf spiralförmige Weise. Wie man sieht, hat die projektive Transformation die Flexibilität, der Landschaft des Vektorraums eine andere Form zu geben und folglich viel mehr strukturelle Information im Vektorraum zu codieren.
Formulierung der projektiven Transformation
Projektgeometrie ist die Art der Geometrie, in der sich parallele Linie im Unendlichen schneiden, das auch der Art und Weise entspricht, wie wir Menschen die Welt sehen. In unserem neuen KGE-Modell (5*E) nutzen wir komplexe Zahlen mit realen und imaginären Teilen in projektiver Geometrie. Wir werden hier einmal zeigen, wie die Transformation durchgeführt wird. Eine komplexe Zahl wird durch einen Punkt in einer komplexen Ebene dargestellt, die man unten sehen kann. Die Transformation funktioniert indem zuerst ein Punkt in der komplexen Ebene auf einen Punkt in der Kugel projiziert wird. Das ist die sogenannte„Riemannsche Zahlenkugel“, welche eine Darstellung für komplexe Zahlen ist, die bis ins Unendliche erweitert sind. Wir verschieben die Kugel dann im zweiten Schritt in eine neue Position und im dritten Schritt projizieren wir das Ergebnis zurück in die komplexe Ebene.
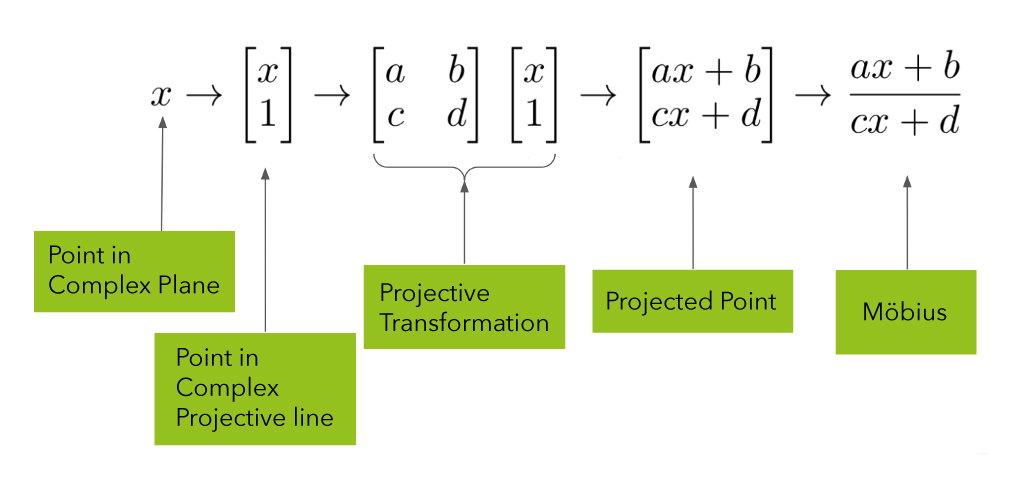
Abbildung 4: Von der projektiven Transformation zu Möbius
5* E Einbettung von Wissensgraphen
Im Folgenden zeigen wir die stereografische Projektion, um die Knoten abzubilden. Die von 5*E durchgeführte beziehungsspezifische Transformation kann als Zusammensetzung von drei Transformationen dargestellt werden (siehe Abbildung und nachstehendes Video):
- Die ursprüngliche Kopfeinbettung wird zunächst von der komplexen Ebene auf die Riemannsche Zahlenkugel abgebildet, die auf der rechten Seite der Abbildung dargestellt ist.
- Die Kugel wird dann an eine neue Position verschoben.
- Der Punkt auf der bewegten Kugel wird dann, durch die Verwendung von stereografischer Projektion, von der Kugel auf die komplexe Ebene abgebildet. Um „head-to-tail”-Entitäten abzubilden, wird daher eine komplexere Transformation durchgeführt, die die Erfassung komplexerer Strukturen ermöglicht.
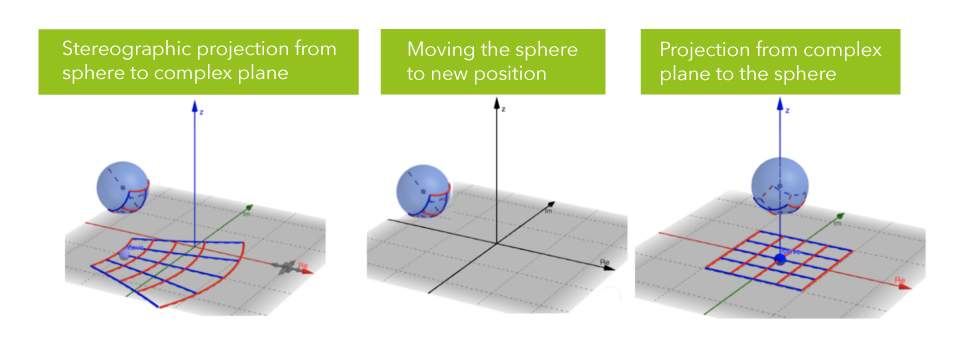
Abbildung 5: Beziehungsspezifische Abbildung von Möbius
Die beziehungsspezifische Transformation in 5*E kann als Zusammensetzung von Übersetzung, Rotation, Homothetie, Reflexion und Inversion dargestellt werden. Wie man sieht, ist die linke Seite eine komplexe Ebene und die rechte Seite eine Ebene mit einer Riemannschen Zahlenkugel in einem dreidimensionalen Raum. Die Übersetzung erfolgt durch das Bewegen der Kugel von einer Position zur anderen. Die Homothetik wird durchgeführt, indem die Kugel entlang der z-Achse bewegt wird, was zu einer Änderung der Größe der Form in der komplexen Ebene führt. Die Rotation der Form in der Ebene erfolgt durch das Drehen der Kugel um die z-Achse. Inversion und Reflexion werden durch die Drehung der Kugel um die reale oder imaginäre Achse gezeigt.
Evaluation und Ergebnisse
Wir haben das Verhalten von 5E sowohl auf Entitätsebene als auch auf Beziehungsebene analysiert. Dabei haben wir die Änderungen für inverse Beziehungen erfasst. Wir haben ein Gitter in die gelernte Transformation des 5E Modells für Teil- und Haspart-Beziehungen sowie Hypernym- und Hyponym-Beziehungen eingefügt, die in inverser Beziehung zueinanderstehen. Invers zueinander sind hier die Linien, die auf den Kreisen abgebildet sind, und die von den einzelnen Paaren erlernte Transformation.
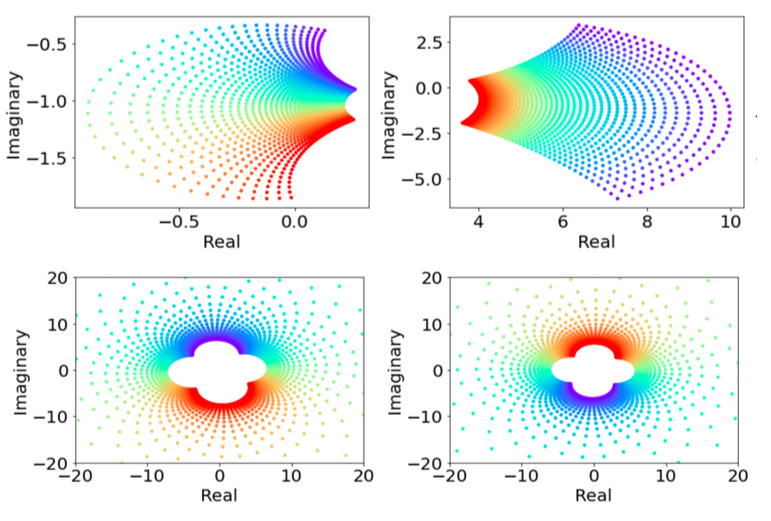
Abbildung 6: Illustration der Transformationen auf Entitätsebene durch 5*E
Hier sind Beispielvisualisierungen für Transformationen in einem Wissensgraphen. Auf der linken Seite sieht man die Einbettungen von Beziehungen, oben ein Raster von komplexen Zahlen. Jeder Punkt auf dem Raster kann eine Dimension einer eingebetteten Entität sein. Unten kann man erkennen, wie die Punkte über die beziehungsspezifische Transformation transformiert werden. Diese Abbildung stammt aus dem WordNet-Wissensgraphen und man kann hier die inversen Beziehungen Hypernym und Hyponym sehen. Invers bedeutet, dass immer dann, wenn A ein Hypernym von B ist, B ein Hyponym von A ist. Was hier sehr schön ist, ist, dass dieses Inversionsmuster als Reflexion im Einbettungsraum modelliert wird. Dies zeigt, dass das Modell diese inverse Beziehung im Einbettungsraum beibehalten kann.
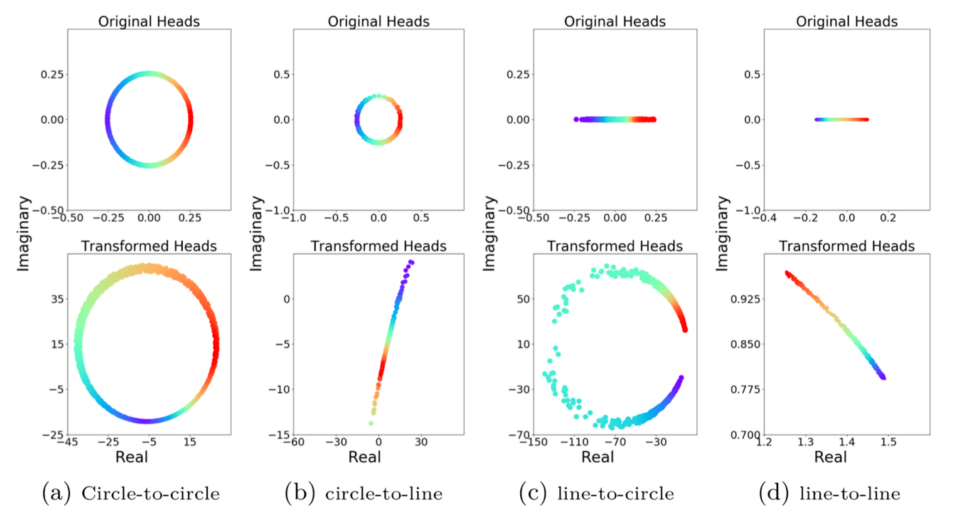
Abbildung 7: Darstellung der Transformationen auf Beziehungsebene durch 5*E
Auf der rechten Seite oben sieht man die Einbettung von Entitäten. Diese werden in die Einbettung unten umgewandelt. Der interessante Aspekt hier ist, dass Linien in Kreise und Kreise in Linien transformiert werden. Kein anderes Modell kann dies und es beeinflusst die Strukturerhaltung im Wissensgraphen.
Abgesehen von der Leistung in der Praxis, ist es eine schöne Sache, dass wir auch einige formale Eigenschaften nachweisen konnten. In unserem Paper konnten wir zeigen, dass das Modell völlig aussagekräftig ist. Ein Modell ist völlig aussagekräftig, wenn es vorhandene und nicht vorhandene Tripel für einen beliebigen Wissensgraphen genau trennen kann.
Wir konnten auch belegen, dass das Modell mehrere relationale Muster (insbesondere Regelzusammensetzung, inverse Regeln und symmetrische Regeln) ableiten kann. Inferenz heißt hier, dass wenn die Prämisse gemäß der Bewertungsfunktion des Modells wahr ist, auch die Schlussfolgerung wahr ist.
Zu guter Letzt konnten wir zeigen, dass das Modell verschiedene Modelle auf dem neuesten Stand der Technik subsumiert. Subsumiert bedeutet an dieser Stelle, dass jede Auswertung für einen beliebigen Wissensgraphen eines Modells durch das allgemeinere Modell erreicht werden kann. Im Wesentlichen ist damit gemeint, dass alle anderen Modelle Sonderfälle des vorgeschlagenen Modells sind.
Mehr Informationen zu der zugehörigen Publikation:
5* Knowledge Graph Embeddings with Projective Transformations.
Nayyeri, M., Vahdati, S., Aykul, C., & Lehmann, J., arXiv preprint, 2020, PDF
Dies war ein Gastbeitrag des SDA Blogs. Hier geht es zur englischen Version des Blogbeitrags: Link