Die Digitalisierung hat in den letzten Dekaden eine immer größere Bedeutung erlangt und verändert nahezu alle Bereiche unseres Lebens. Einer der Bereiche, in denen die Digitalisierung besonders große Fortschritte ermöglicht hat, ist das Maschinelle Lernen (ML). Durch die Bereitstellung von immer größeren Datenmengen und immer mehr Rechenleistung können heute komplexe Algorithmen angewendet werden. Jedoch gehen mit größeren Datenmengen auch Herausforderungen einher, zum Beispiel bei der Verarbeitung. Eine zentrale Herausforderung bei der Verarbeitung ist hier die Reduktion der Dimensionalität. Eine Möglichkeit der Dimensionsreduktion ist die Linear Discriminant Analysis, zu Deutsch: Lineare Diskriminanzanalyse (LDA). Im Folgenden erfahren Sie, wie LDA als Werkzeug zur Dimensionsreduktion von großen, hochdimensionalen Daten eingesetzt werden kann und warum die Dimensionsreduktion ein wichtiger Bestandteil des Maschinellen Lernens ist, um den Curse of Dimensionality zu überwinden.
Was ist Dimensionsreduktion?
Die Dimensionsreduktion ist ein Verfahren, bei dem die Anzahl der Merkmale, auch genannt die Dimensionen eines Datensatzes, reduziert wird. Dabei ist das Ziel, die Komplexität des Datensatzes zu verringern und somit eine bessere Analyse und Interpretation der Daten zu ermöglichen. Ein wichtiger Grund für die Anwendung von Dimensionsreduktion ist der Curse of Dimensionality (zu Deutsch: Fluch der Dimensionalität). Dieser besagt, dass je mehr Dimensionen ein Datensatz hat, desto mehr Datenpunkte braucht es, um verlässliche Aussagen über Muster und Zusammenhänge in den Daten treffen zu können.
Durch die Anwendung von Dimensionsreduktionstechniken wie der Principal Component Analysis (PCA) oder der Linear Discriminant Analysis (LDA) kann die Anzahl der Dimensionen in einem Datensatz reduziert werden. Hierbei werden neue Merkmale geschaffen, die aus einer Kombination der ursprünglichen Merkmale entstehen. Dabei werden jedoch nur die wichtigsten Informationen in den neuen Merkmalen berücksichtigt, um eine möglichst genaue Darstellung der Daten zu erhalten (erfahren Sie in diesem Beitrag mehr darüber, wie viele Daten Künstliche Intelligenz wirklich braucht).
Dimensionsreduktion ist somit ein wichtiger Bestandteil des Maschinellen Lernens, um den Curse of Dimensionality zu überwinden und komplexe Datensätze effektiver analysieren und interpretieren zu können. Welche Merkmale der Daten dabei wichtig sind, entscheidet sich durch den ausgewählten Algorithmus. Ein Algorithmus könnte zum Beispiel das Erkennen der Merkmale, in denen sich die Daten am meisten unterscheiden, als Ziel haben. Auch die Art der Daten, die uns vorliegen, bestimmt, neben dem Ziel unserer Dimensionsreduktion, ebenfalls, welche Algorithmen sich am besten eignen. Man unterscheidet dabei zwischen klassifizierbaren und nicht-klassifizierbaren Daten. Letztere sind Datensätze, deren Datenpunkte nicht in verschiedene Kategorien oder Klassen gruppiert sind. Oftmals ist das Ziel von Dimensionsreduktionsverfahren, die auf nicht-klassifizierbaren Daten arbeiten, eine Analyse der Struktur oder Zusammensetzung des Datensatzes.
Klassifizierbare Datensätze beinhalten stattdessen Datenpunkte, die verschiedenen Klassen zugeordnet sind. Zwei Datenpunkte aus diesen Datensätzen können also nicht nur durch ihre Merkmale verglichen werden, sondern auch durch ihre Label, welche die Informationen über die zugeordneten Klassen enthalten. Ein Ziel eines Algorithmus, der auf Basis von klassifizierbaren Daten arbeitet, könnte zum Beispiel sein, die Datenpunkte verschiedener Klassen zu separieren (mehr zum Thema Klassifikation lesen Sie im Grundlagenbeitrag Klassifikation im Maschinellen Lernen).
Merkmale auswählen oder kombinieren?
Die Vorgehensweisen der Dimensionsreduktionsverfahren unterscheidet man in zwei Arten. Dabei ist es wichtig, wie die resultierenden Merkmale der Dimensionsreduktion aussehen.
Bei der sogenannten Merkmalsauswahl wird die Reduktion durch Weglassen von unwichtigen Merkmalen durchgeführt. Dafür müssen die Merkmale im Vorhinein durch einen Algorithmus bewertet werden, sodass die unwichtigeren Merkmale nicht in den reduzierten Datensatz übernommen werden. Algorithmen zur Merkmalsprojektion reduzieren den Datensatz durch die Kombination mehrerer Merkmale. Das Ziel der LDA ist es, die Merkmale so zu reduzieren, dass die reduzierten Datenpunkte optimal durch eine Gerade trennbar sind.
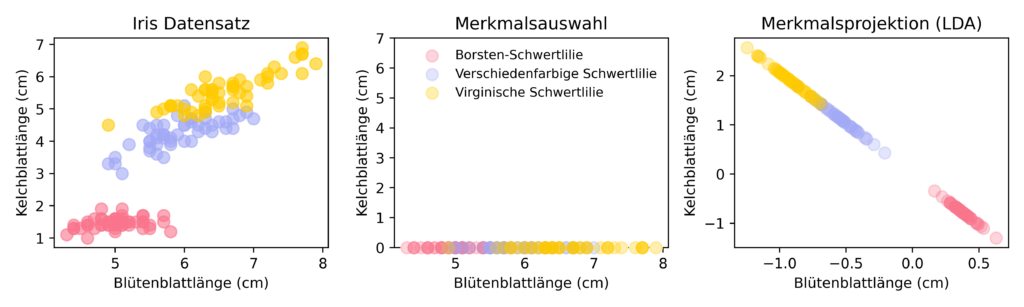
Abbildung 1: Am Beispiel eines Datensatzes über die Iris, eine Pflanzengattung innerhalb der Familie der Schwertliliengewächse, wird der Unterschied zwischen einem Algorithmus zur Merkmalsauswahl und Merkmalsprojektion (LDA) aufgezeigt.
Abbildung 1 zeigt einen Datensatz mit Datenpunkten von drei verschiedenen Schwertlilienarten und die Ergebnisse der Dimensionsreduktion durch die Merkmalsauswahl sowie durch die Merkmalsprojektion. Die Datenpunkte aus dem Iris-Datensatz werden durch zwei Merkmale beschrieben, die Blütenblattlänge und die Kelchblattlänge und liegen in einer zweidimensionalen Fläche vor.
Bei der Merkmalsauswahl entscheiden wir uns für das Merkmal Blütenblattlänge. Die Informationen über die Kelchblattlänge gehen dabei verloren und unsere Daten werden nur noch durch ein Merkmal beschrieben. Sie liegen in einer eindimensionalen Geraden vor. Man kann außerdem erkennen, dass die Auswahl des Merkmals „Kelchblattlänge“ die Daten der Klassen besser separieren würde.
Im Fall der Merkmalsprojektion (LDA) liegen die Daten auch in einer eindimensionalen Geraden vor. Hierbei sind, anders als bei der Merkmalsauswahl, die Informationen beider Merkmale in die Reduktion eingeflossen. Es fällt auf, dass die einzelnen Klassen durch die Merkmalsprojektion besser separiert wurden als durch das Verfahren der Merkmalsauswahl. Jedoch kann man auch erkennen, dass die Werte der reduzierten Merkmale, im Gegensatz zur Blütenblattlänge bei der Merkmalsauswahl, stark von den ursprünglichen Werten abweichen.
Die Lineare Diskriminanten Analyse (LDA)
LDA ist ein Merkmalsprojektions-Algorithmus zur Dimensionsreduktion, welcher auf Basis von klassifizierbaren Daten arbeitet. Das bedeutet, dass es sich bei LDA um eine Methode handelt, bei der die ursprünglichen Merkmale in einem Datensatz auf eine kleinere Anzahl von neuen Merkmalen projiziert werden. Ihr Ziel ist es, die neuen Merkmale so zu wählen, dass sie die bestmögliche Trennung zwischen verschiedenen Klassen innerhalb der Daten ermöglichen.
LDA erreicht dieses Ziel durch die Betrachtung von Streuungen im Datensatz. Zum einen soll die Streuung zwischen verschiedenen Klassen (Zwischenklassenvarianz) maximiert, zum anderen die Streuung innerhalb einer Klasse (Innerklassenvarianz) minimiert werden. Das heißt, wir suchen eine Sicht auf die Daten, in denen die Datenpunkte verschiedener Klassen möglichst weit auseinander liegen und die Daten derselben Klasse möglichst nah beieinander sind.

Abbildung 2: Darstellung der Funktionsweise eines LDA-Algorithmus.
Durch die Kombination von Maximierung der Zwischenklassenvarianz und Minimierung der Innerklassenvarianz werden die neuen Variablen so gewählt, dass sie die bestmögliche Trennung zwischen den Klassen im Datensatz ermöglichen (siehe Abbildung 2).
Grenzen und Einschränkungen
Obwohl die Dimensionsreduktion eine nützliche Methode ist, um komplexe Daten zu analysieren und zu visualisieren, gibt es folgende Grenzen und Einschränkungen zu beachten:
- Generell lässt sich feststellen, dass mit der Reduktion von Daten immer ein Informationsverlust einhergeht. Das kann zu einer unvollständigen oder ungenauen Analyse führen. Die Reduktion gelingt am besten, wenn sich der ursprünglichen Datensatz sowieso durch weniger Merkmale oder Dimensionen beschreiben lässt.
- Die Genauigkeit der Linear Discriminant Analysis hängt auch von Faktoren wie der Anzahl der Datenpunkte und der Menge der Ausreißer im Datensatz ab. Zu wenige Datenpunkte können zum Overfitting führen, das heißt dass durch die Reduktion die verbleibenden Merkmale zu stark auf die Stichprobe zugeschnitten werden. Das Modell kann dann auf weitere Daten nicht gut übertragen werden. Ausreißer hingegen führen zu einer grundsätzlichen Verzerrung der Ergebnisse.
- Es ist daher wichtig, Ausreißer im Datensatz zu identifizieren und zu entfernen, bevor die Dimensionsreduktion durchgeführt wird.
- Vor allem aber funktioniert die LDA nicht, wenn sich die Zentren der verschiedenen Klassen überlappen oder ihre Datenpunkte stark vermischt sind.
- In Abbildung 3 sind die Ursprungsdaten so stark vermischt, dass durch die Dimensionsreduktion mit LDA keine Separation der Klassen möglich ist. Es gibt also Fälle, in denen Dimensionsreduktion nicht empfehlenswert ist, da sonst die Eigenschaften der Daten verfälscht werden und ML-Algorithmen schlechtere Ergebnisse liefern.
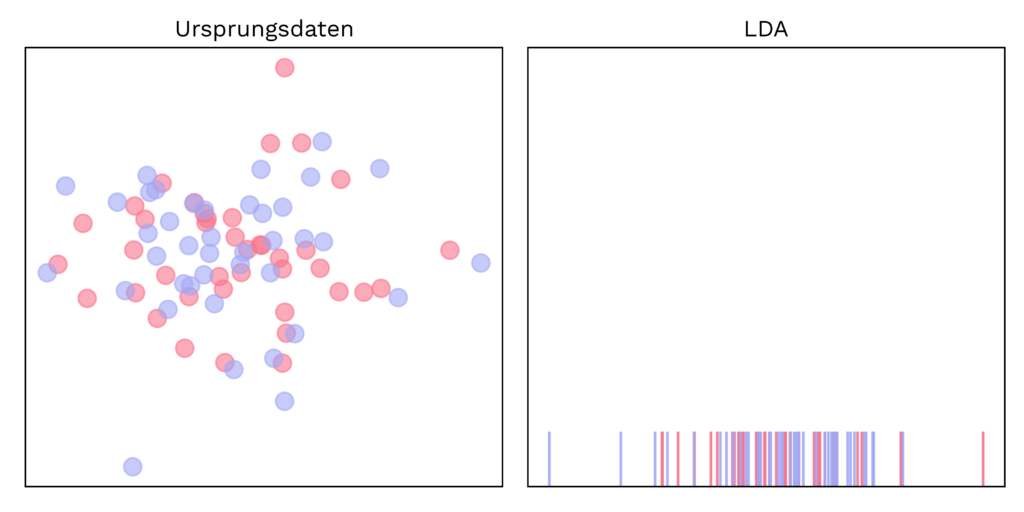
Abbildung 3: Die Ursprungsdaten sind hier so stark vermischt, dass durch die Dimensionsreduktion mit LDA keine Separation der Klassen stattfindet. Die Genauigkeit der Daten wird verfälscht und der ML-Algorithmus liefert schlechtere Ergebnisse.
Dimensionsreduktion als Vorverarbeitung für ML-Algorithmen
Abschließend lässt sich zusammenfassen, dass es verschiedene Dimensionsreduktionsverfahren für unterschiedliche Probleme und Ziele gibt. Die Algorithmen zur Merkmalsauswahl und -projektion können entweder auf nicht-klassifizierbaren oder klassifizierbaren Daten angewandt werden und durch die Reduktion der Merkmale die Datenlast für ML-Algorithmen reduzieren. Insbesondere LDA kann klassifizierbare Daten analysieren und eine lineare Separation ermöglichen. Jedoch sollten die Grenzen und Einschränkungen bei der Anwendung von LDA stets berücksichtigt werden, da nicht jedes Verfahren für jeden Datensatz sinnvoll ist.
