Mit dem Voranschreiten der Digitalisierung in unserer Gesellschaft ist die vorhandene Menge gesammelter Daten heutzutage enorm groß. Besondere Relevanz hat das unter anderem für das Maschinelle Lernen, denn hier führen große Datenmengen im Allgemeinen zu aussagekräftigeren Ergebnissen (mehr zur Größe der Trainingsdaten beim Maschinellen Lernen lesen Sie im Grundlagenbeitrag Wie viele Daten braucht Künstliche Intelligenz?). Dies wirkt sich jedoch entscheidend auf die Rechenzeit- und Speicherkomplexität aus, die für das Training eines Lernalgorithmus benötigt wird – und in vielen Fällen können diese Anforderungen (z. B. in Echtzeitanwendungen) gar nicht erfüllt werden. Hier kann die Hauptkomponentenanalyse zur Lösung des Problems beitragen. Erfahren Sie im Folgenden, wie dieses Werkzeug zur Dimensionsreduktion von großen, hochdimensionalen Datenmengen funktioniert.
Was ist Dimensionsreduktion?
Anstatt nun die Menge an Datenpunkten zu reduzieren, auf denen der Algorithmus lernt, was sich negativ auf die Qualität des trainierten Lerners auswirken könnte, nutzen wir ein anderes Verfahren. Denn es ist genauso möglich, die Anzahl an Merkmalen der gegebenen Daten zu verringern. Die Anzahl der Merkmale wird auch als die Dimensionalität der Daten bezeichnet.
Es existieren zwei grundlegende Verfahren, um die Dimensionalität einer Datenmenge zu reduzieren, die sowohl bei der Datenanalyse als auch zur Vorverarbeitung für ML-Algorithmen eingesetzt werden:
- Merkmalsauswahl: Darunter ist das Vorgehen zu verstehen, lediglich eine Teilmenge der vorhandenen Merkmale auszuwählen und anschließend die Daten nur durch die ausgewählten Merkmale zu beschreiben.
- Merkmalsprojektion: Hierbei wird jeder Datenpunkt auf einen Punkt mit weniger Merkmalen projiziert.
Wichtig ist hierbei, dass die Merkmale des reduzierten Punkts nicht den ursprünglichen Merkmalen entsprechen – lediglich der reduzierte Punkt als Ganzes muss seinem Pendant aus der Menge der Ausgangspunkte ähneln.
Dimensionsreduktion durch Projektion
Um die Hauptkomponentenanalyse und allgemein den Bereich der Merkmalsprojektion besser zu verstehen, ist ein genaueres Verständnis des (mathematischen) Begriffs der Projektion von Nutzen. Schauen wir uns also an, was darunter zu verstehen ist: Eine Projektion ist eine Funktion, die einen Eingabepunkt so verändert, dass er mit weniger Komponenten beschreibbar ist. Dies kann als eine Art Schattenwurf verstanden werden: Der Schatten eines ursprünglich dreidimensionalen Punktes kann sowohl als anderer dreidimensionaler Punkt im gleichen Raum dargestellt werden – abhängig von der Lichtquelle und der Oberfläche, auf die der Schatten geworfen wird. Oder er kann alternativ auch als zweidimensionaler Punkt in der Ebene, auf die der Schatten geworfen wird, abgebildet werden.
Um dies an einem Beispiel zu illustrieren, sehen wir uns einen herkömmlichen Würfel an, der von einer Lichtquelle angestrahlt wird und seinen Schatten auf den Boden wirft, auf dem er liegt.

Figur 1: Skizze eines Würfelschattens
Fassen wir den Würfel als eine Menge von Punkten im dreidimensionalen Raum auf, so ist sein Schatten die Menge von Punkten, die entsteht, wenn man die ursprünglichen Punkte auf die zweidimensionale Ebene projiziert, die durch den Boden vorgegeben ist. Diese Projektionsebene wird durch die Projektionsfunktion definiert und muss nicht zwangsläufig zweidimensional sein. Daher bezeichnet man die Fläche, auf die projiziert wird, auch allgemein als Unterraum. Dessen Dimensionalität bestimmt die reduzierte Dimension der Datenpunkte. Ferner kann der Schattenwurf (auf die gleiche zweidimensionale Ebene) durch Bewegung der Lichtquelle an eine andere Position verändert werden. Zentrieren wir die Lichtquelle über dem Würfel so, dass der Würfel genau zwischen Boden und Lichtquelle steht, befindet sich sein Schatten direkt unter dem Würfel. Da bei dieser Projektion die Verbindungslinie von einem ursprünglichen Würfelpunkt zu seinem korrespondierendem Schattenpunkt genau orthogonal (also im 90-Grad-Winkel) zum Boden, also der Projektionsfläche ist, sprechen wir in diesem Fall von einer sogenannten Orthogonalprojektion.
Da solche Orthogonalprojektionen den Abstand zwischen einem ursprünglichen Punkt und seinem korrespondierenden Schattenpunkt (per Satz des Pythagoras) minimieren, also damit die Information des ursprünglichen Punktes möglichst erhalten, beschränkt sich die im folgenden erläuterte Methode zur Reduktion ausschließlich auf die Suche nach der bestmöglichen Orthogonalprojektion.
Principal Component Analysis
Ein Beispiel für eine solche Dimensionsreduktion durch Projektion ist die Principal Component Analysis (dt. Hauptkomponentenanalyse) oder auch kurz PCA genannt. Sie projiziert eine Menge gegebener Datenpunkte in einen Unterraum, wobei der Unterraum so gewählt wird, dass die Varianz der orthogonal projizierten Datenpunkte maximal ist. Durch die maximale Streuung der reduzierten Datenpunkte lässt sich im Fall klassifizierter Daten damit eine gute Separierbarkeit der verschiedenen Klassen erhoffen (Klassifikation beim Maschinellen Lernen). Die Dimension $k$ des Unterraums wird vom Anwender der PCA vorgegeben und bestimmt, durch wie viele Koordinatenachsen der Unterraum beschrieben wird. Diese $k$ Koordinatenachsen werden auch als Hauptkomponenten bezeichnet.
Ist eine visuelle Inspektion der Daten möglich, haben die Ausgangsdaten also höchstens Dimension drei, lässt sich die erste Hauptkomponente als die Richtung der größten Streuung der Daten erkennen. Die jeweils nächste Hauptkomponente zeigt in die Richtung der nächstgrößeren Streuung der Daten, mit der Nebenbedingung, dass sie orthogonal zu allen bisherigen Hauptkomponenten ist. Um dieses Verfahren an einem Beispiel zu demonstrieren, verwenden wir Fisher’s Iris Datensatz – ein unter Datenwissenschaftler*innen bekannter Datensatz – der mit 150 Beispielen mit je vier Merkmalen drei verschiedene Arten von Schwertlilien beschreibt. Wir beschränken uns aus Visualisierungsgründen im folgenden Beispiel auf zwei der Merkmale. Hierbei sind die beiden Merkmale die Messungen der Blütenblattbreite und Blütenblattlänge der jeweiligen erfassten Pflanzen.
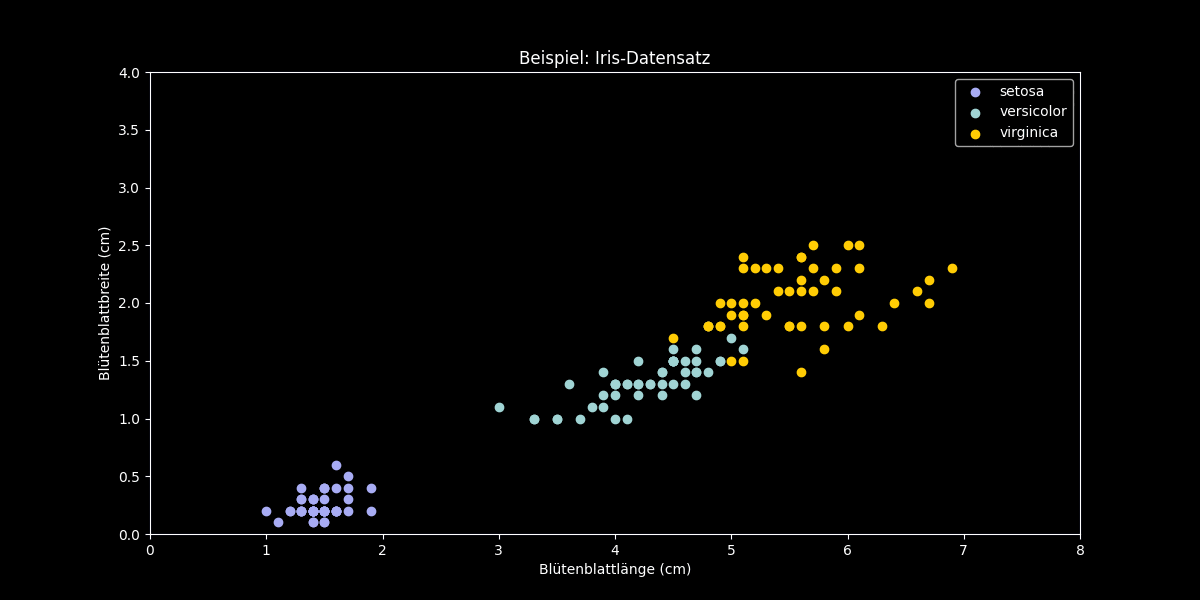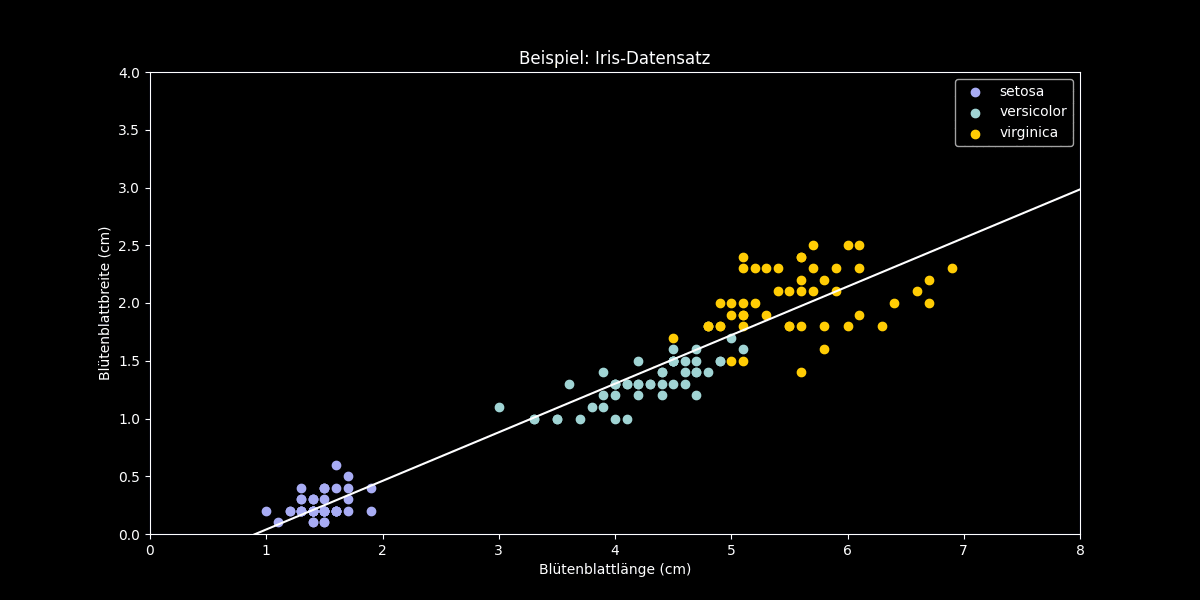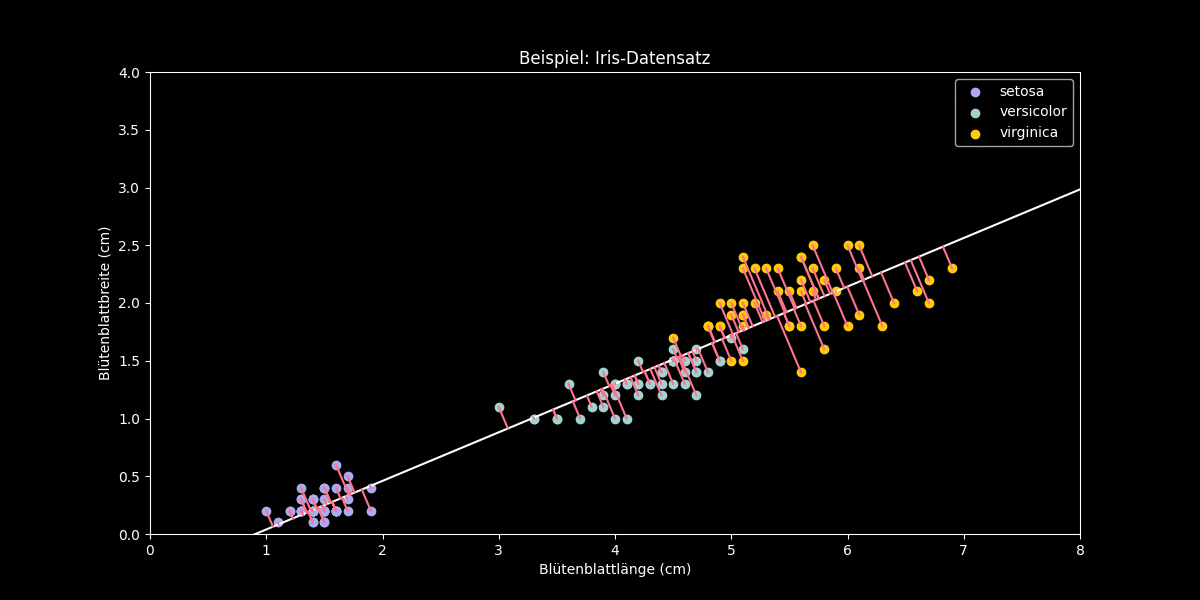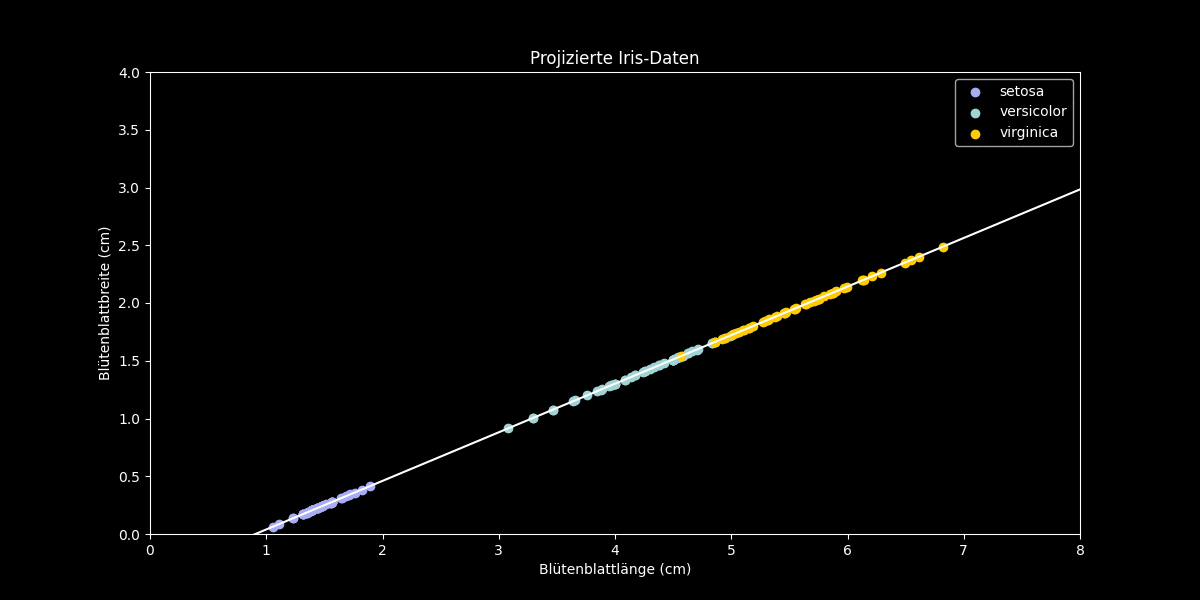
Figur 2: Hauptkomponentenanalyse am Beispiel des Iris-Datensatzes
Nun wenden wir die PCA auf dieses Beispiel an, um die Daten auf Dimension $k = 1$ zu reduzieren. Dazu suchen wir diejenige Gerade durch die Daten, welche die Varianz der (orthogonal) projizierten Datenpunkte maximiert. Diese Gerade repräsentiert also den eindimensionalen Unterraum, auf den die PCA die Datenpunkte projiziert. Obiges Beispiel zeigt, dass selbst nach der Dimensionsreduktion die Klassen noch recht gut voneinander unterscheidbar sind.
Dies ist jedoch nicht immer der Fall. Ferner kann die Anwendung der PCA auf klassifizierte Daten dazu führen, dass vorher unterscheidbare Klassen nach der Dimensionsreduktion völlig überlappen und somit keine klaren Unterschiede zwischen den Klassen zu erkennen sind. Dafür betrachten wir erneut eine Menge zweidimensionaler Datenpunkte von fiktiven Messwerten zu drei verschiedenen Pflanzentypen:
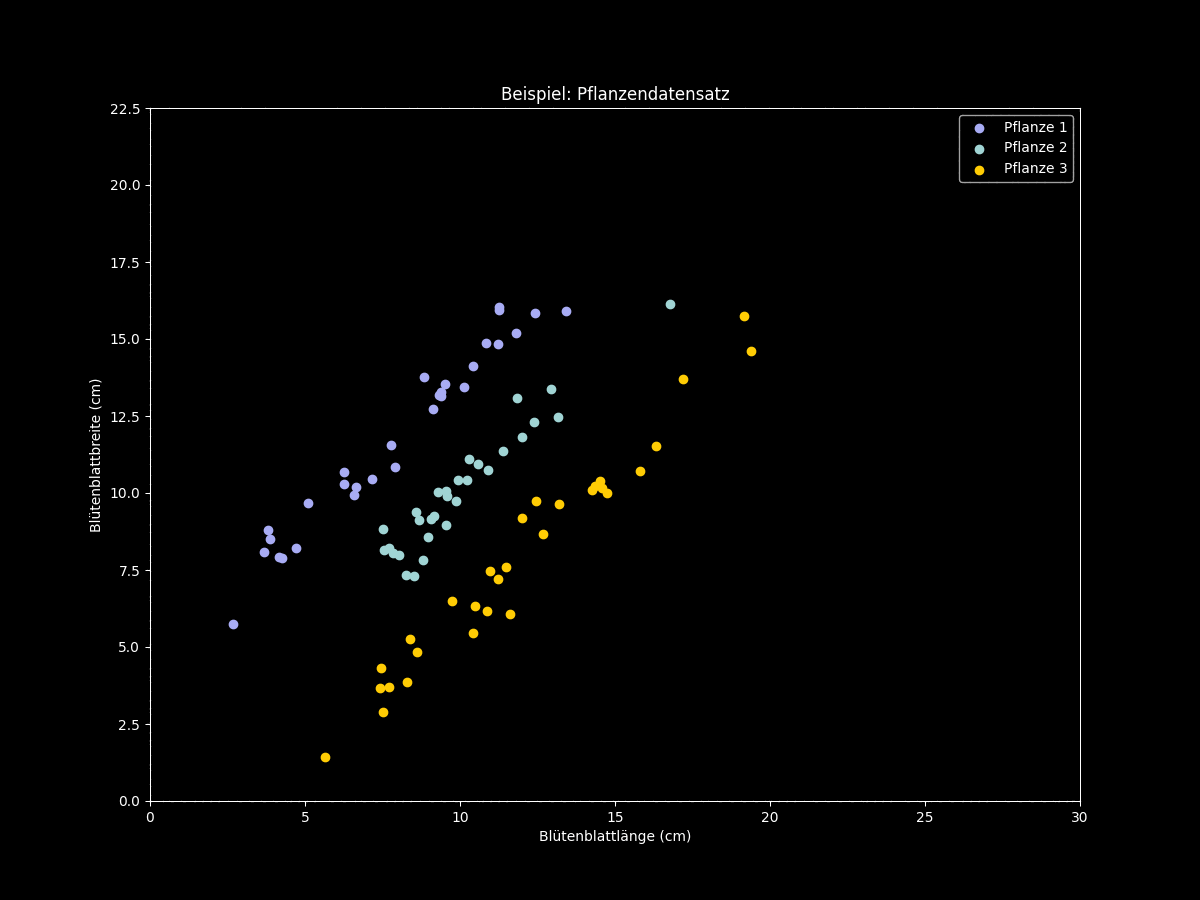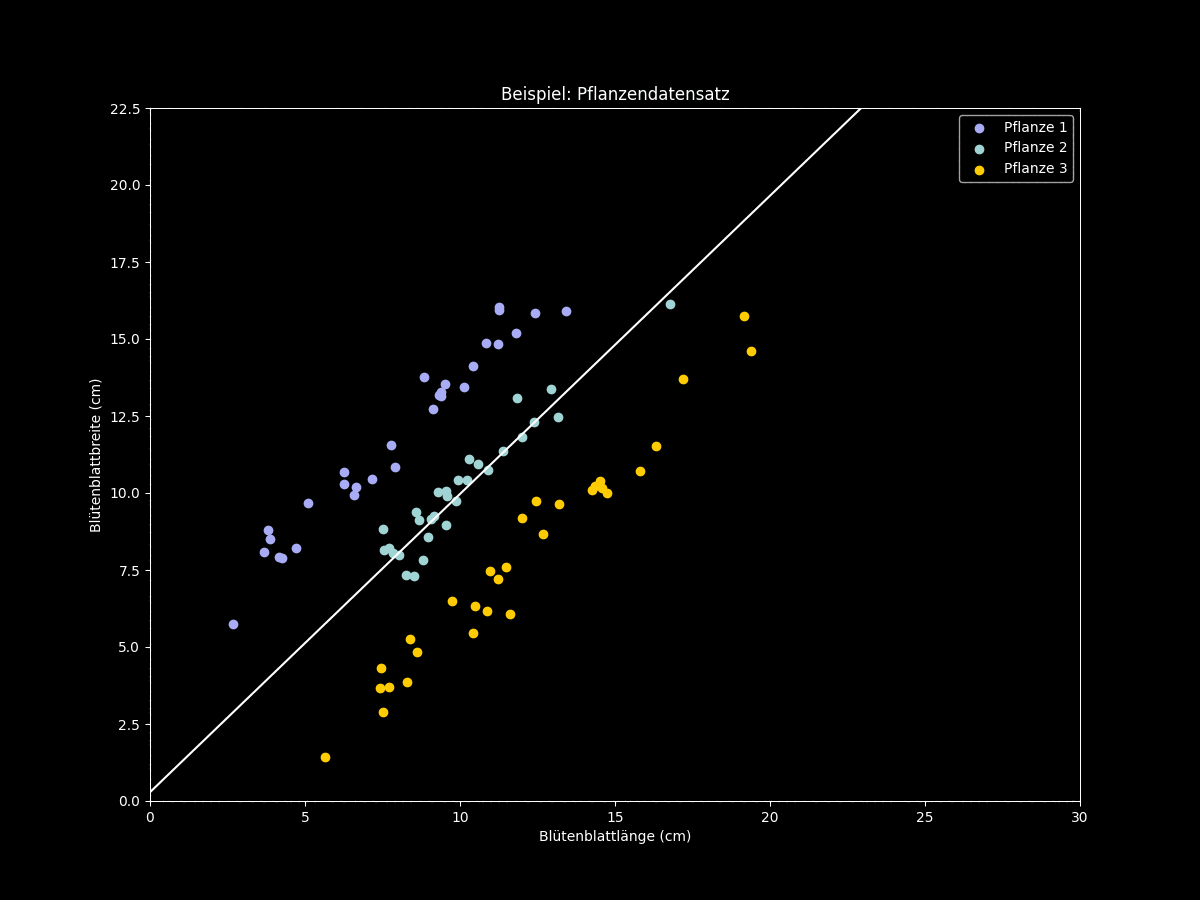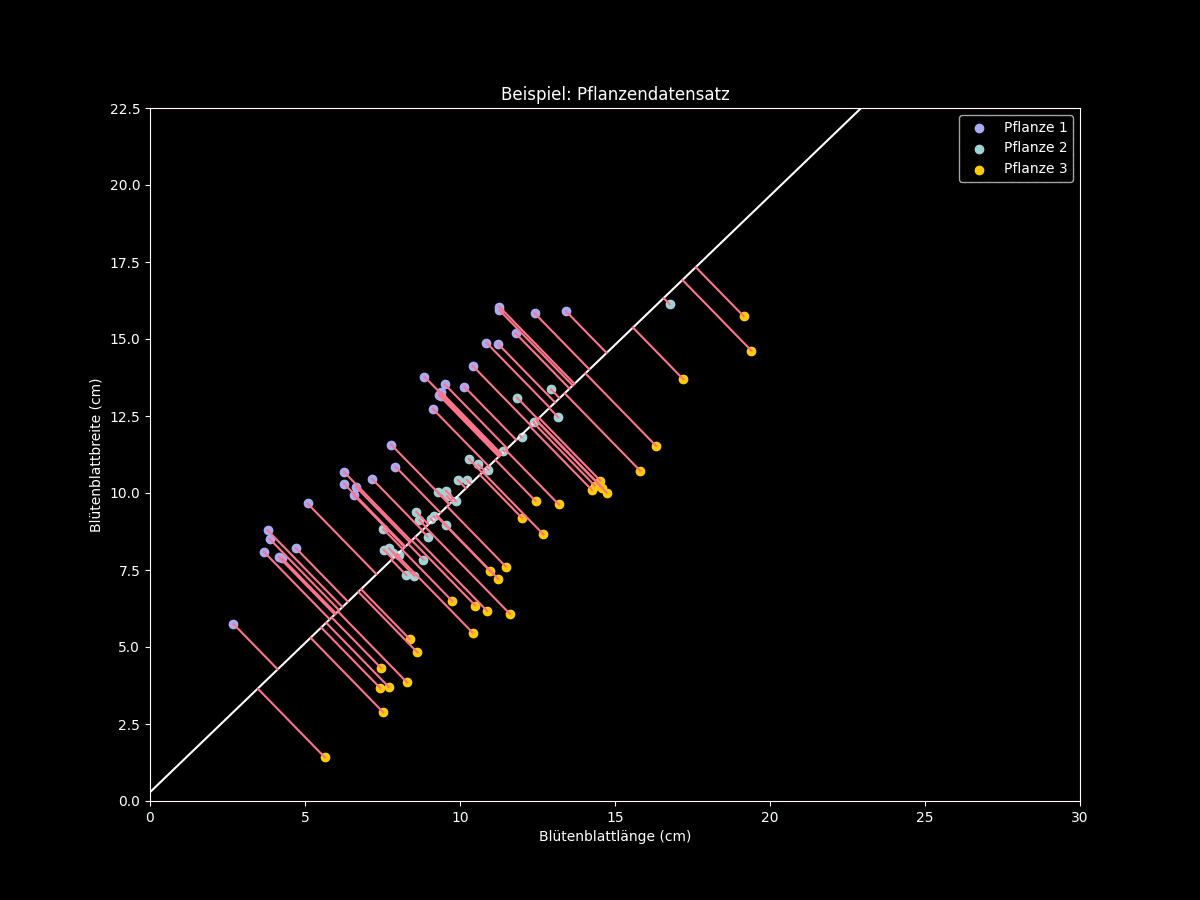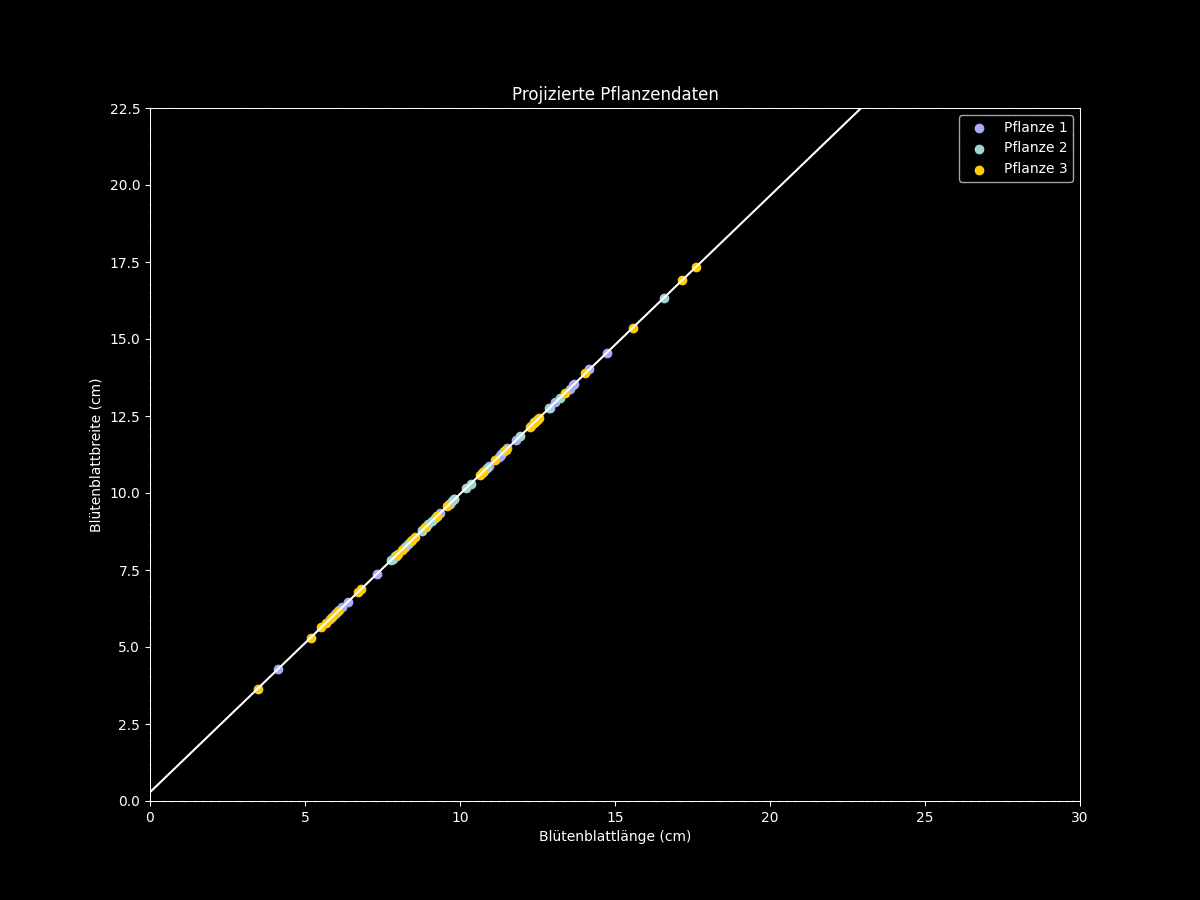
Figur 3: Hauptkomponentenanalyse bei ungünstigen Beispieldaten
Das letzte Beispiel zeigt, dass die Hauptkomponentenanalyse – vor allem als Zwischenschritt in einem Klassifikationsproblem – mit Vorsicht angewandt werden sollte.
Fazit
Dimensionsreduktion ist ein wichtiges Teilgebiet des Maschinellen Lernens. Neben einer Verringerung von Rechenzeit- und Speicherplatzbedarf kann auch unerwünschtem Rauschen entgegengewirkt werden. Im Wesentlichen ist Dimensionsreduktion nichts anderes als eine Reduktion der Anzahl der Merkmale einer gegebenen Datenmenge. Dabei wird grundsätzlich zwischen den Methoden der Merkmalsauswahl und der Merkmalsprojektion unterschieden. Die Principal Component Analysis ist ein Beispiel für letztere, welche die Daten auf den Unterraum projiziert, der die meiste Varianz der Daten enthält.
Nächste Woche wird es erneut um die Dimensionsreduktion von großen Datensätzen gehen. Dann stellen wir ein weiteres Verfahren sowie dessen Vor- und Nachteile vor.
