
Methoden aus den Bereichen Künstliche Intelligenz und Maschinelles Lernen stehen allgemein im Ruf, viele Daten zu benötigen. Aber was bedeutet das konkret? In Schulungen oder im Gespräch mit Anwender*innen begegnen uns häufig genau diese Fragen: Was sind „viele“ Daten? Wie viele Daten brauche ich mindestens für ein gutes Modell? Welche Faktoren haben Einfluss auf die Menge der Daten? In diesem Beitrag möchten wir dieses Thema diskutieren. Er soll Hilfestellung geben, die eigenen Herausforderungen einzuschätzen und Einblick geben, wie ein Data Scientist auf die verschiedenen Anwendungsprobleme schaut.
Warum benötigt ein Modell des Maschinellen Lernens so viele Daten?
Zuallererst wollen wir erklären, warum ein Modell des Maschinellen Lernens überhaupt viele Daten zum Training benötigt. Ein Grund liegt im sogenannten „Curse of Dimensionality“ (Fluch der Dimensionalität). Der „Curse of Dimensionality“ beschreibt das exponentielle Wachstum des Raums und damit der Daten, die man benötigt, um ihn zu füllen, in Abhängigkeit der Anzahl an Eingangsgrößen.
Ein Beispiel hierfür ist der Kauf einer neuen Kaffeemaschine mit einer Unmenge von binären Schaltern, bei der die Anleitung verloren gegangen ist. Wie kann man herausfinden, bei welchen Schalterpositionen der Kaffee schmeckt und welche Einstellungen vermieden werden sollten? Bei nur einem Schalter kann man es einfach ausprobieren – hierfür müsste man zwei Tassen Kaffee trinken und diese vergleichen. Bei zwei Schaltern werden es für alle An-/Aus-Kombinationen vier Tassen, bei drei Schaltern acht Tassen. Die Anzahl der Versuche wächst somit mit 2{Anzahl der Schalter}. Bei 20 Schaltern sind dies schon 1.048.576 Tassen Kaffee. Wenn nun alle Schalter nicht nur binär sind, sondern (N) Einstellungen haben, ergibt sich ein Zusammenhang von (N{Anzahl der Schalter}). Das bedeutet für fünf Einstellungen mit fünf Schaltern benötigt man 3.125 Versuche, um herauszufinden, welche Einstellung die richtige ist.
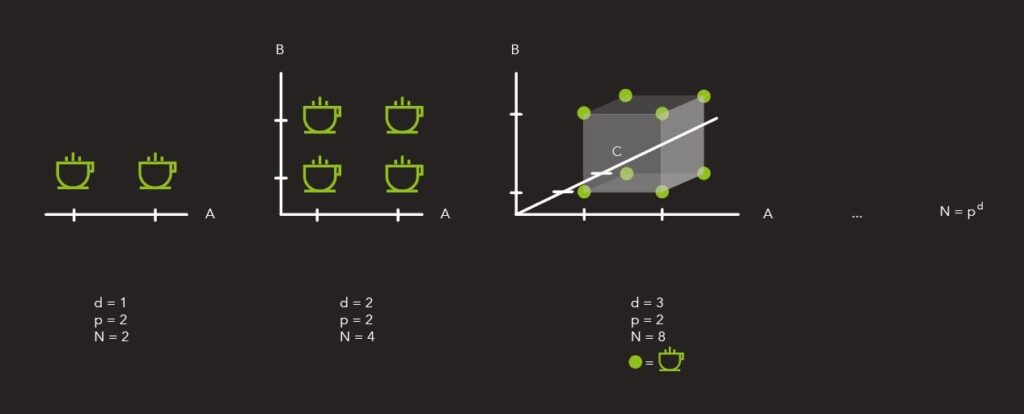
Eine Abbildung des Curse of Dimensionality. Für eine verschiedene Anzahl der Dimensionen d und der Diskretisierungen p wird die Anzahl der benötigten Datenpunkte N gezeigt.
Wenn wir jetzt ein ML-Modell für den Kaffeegeschmack in Abhängigkeit der Schalter entwickeln wollen, benötigen wir die Versuchsdaten Schaltereinstellung –> Kaffeegeschmack. Wenn das Modell sehr einfach, aber dennoch sehr exakt sein soll, würden wir eines bauen, das in den Versuchsdaten nachschaut, welcher Geschmack sich aus der aktuellen Schaltereinstellung ergibt. Die Stärke von Maschinellem Lernen ist jedoch die Generalisierung, das heißt das Modell kann auf der Basis von gelernten Beispielen Rückschlüsse auf neue Zustände, die nicht Teil des bisher Gelernten sind, ziehen.
Dies würde in unserem Fall bedeuten, dass wir nur einen Teil der Daten benötigen, und das Modell schließt aus ihnen, wie der Kaffee für eine andere Schalterkombination schmeckt. Hier bleibt dann die Frage: Wie viele Datenpunkte brauche ich dann? Um beim Beispiel der 5 Schalter (= 5 Dimensionen) mit 5 Einstellungen (= 5 Diskretisierungen) zu bleiben: Wie viele meiner 3.125 Punkte werden benötigt, um ein gutes Modell für den Kaffeegeschmack in Abhängigkeit der Schalterstellung zu erzeugen?
Wie viel Information benötigt ein ML-Modell?
Um ein Gefühl zu entwickeln, wie viele Daten ein Modell (zum Beispiel der Geschmack des Kaffees in Abhängigkeit der Schalterpositionen) benötigt, schauen wir zunächst auf ein Beispiel mit nur einer Dimension.
Wenn wir wüssten, wie der Prozess, den wir modellieren möchten (die „Ground Truth“), sich verhält, ist das Vorhaben einfacher:

Zwei Extremverhalten für das Verhalten der Ground Truth und die notwendige Abtastung. Links eine sehr einfache Ground Truth: Es reichen zwei Datenpunkte aus, um sie zu schätzen. Rechts eine sehr komplizierte Ground Truth: Es werden sehr viele Datenpunkte benötigt, um nur einen Teil ihres Verhaltens abzubilden.
Im Bild sind zwei Extrembeispiele dargestellt, wie sich ein Prozess abhängig von einem Faktor verhalten könnte. Für einen linearen Zusammenhang (linkes Bild) müssten wir zweimal, für einen sehr unebenen Zusammenhang (rechtes Bild) sehr oft messen. Daraus lässt sich schlussfolgern: Je weniger glatt das Prozessverhalten ist, desto mehr Daten werden benötigt. In der Signalverarbeitung wurde dies im Nyquist-Shannon-Abtasttheorem formuliert. Es besagt, dass ein kontinuierliches Signal (unser Prozess), das eine maximale Frequenz (f_{max}) hat, mit einer Frequenz von größer (2 f_{max}) abgetastet werden muss, um es exakt rekonstruieren zu können. Und diese Rekonstruktion des Signals beziehungsweise Prozesses ist das Ziel des ML-Modells. Es soll aus den Daten für die Schaltereinstellung den Geschmack des Kaffees vorhersagen können. Wenn wir jetzt nicht nur einen ein- sondern mehrdimensionalen Zusammenhang lernen wollten, benötigen wir entsprechend des Curse of Dimensionality exponentiell mehr Daten. Im einfachsten Fall wird die Anzahl der Datenpunkte exponentiell mit der Abtastfrequenz wachsen, also (N = Punktzahl nach Abtastfrequenz^{Dimensionen}).
Tatsächlich ist die Abtastfrequenz in der Realität unbekannt und es werden selten alle Annahmen, die die Grundlage für das Theorem bilden, erfüllt. Jedoch gibt das Theorem eine wissenschaftliche Grundlage für das Bauchgefühl: Wo im Prozess sehr viel passiert, werden auch viele Daten benötigt. Wenn also der Kaffeegeschmack für Schalter A sehr variiert und für die anderen vier Schalter linear ist (egal, wie A steht), werden für die Dimension A sehr viele Daten und für die anderen Dimensionen nur wenig Daten benötigt. In Punkten ausgedrückt, wären wir hier bei (2^4 cdot 5^1 = 320), statt den obigen 3.125 Punkten.
Welche Rolle spielt der Modelltyp?
Nun haben wir über die Daten und den Prozess gesprochen – aber was ist mit dem Unterschied zwischen Neuronalen Netzen, die eher mehr Daten brauchen, zu einfachen linearen Modellen, die weniger Daten benötigen?
Die Antwort liegt darin, welche Prozesse die Modelle abbilden können. Ein lineares Modell wird, egal, wie viele Daten zur Verfügung stehen, immer nur einen linearen Zusammenhang ausdrücken. Mit einer steigenden Anzahl an Daten werden sich seine Parameter (also seine Steigung und sein Offset – der Wert, den das Modell für einen Input von 0 annimmt) nur noch wenig ändern. Es wird also eine begrenzte Anzahl Daten benötigt. Ein Neuronales Netz ist im Gegensatz dazu ein universaler Approximator. Es kann sehr komplexe Zusammenhänge beschreiben und mit einer steigenden Anzahl an Daten werden sich seine Parameter immer wieder ändern. Aber wenn ein Neuronales Netz nur sehr wenige Datenpunkte sieht, wird es auch nur einen einfachen, unter Umständen linearen Zusammenhang finden.
In der Praxis bedeutet dies, dass man die Wahl des Modells von der Anzahl der verfügbaren Datenpunkte abhängig macht. Je mehr Daten zur Verfügung stehen, desto komplexer ist der Zusammenhang, den ich ausdrücken kann, und desto komplexer darf das Modell sein. Die Anzahl der notwendigen Datenpunkte bleibt davon jedoch unberührt. Sie hängt allein vom Prozess ab.
Ein gutes ML-Modell benötigt nicht unbedingt eine große Menge an Daten, sondern genau die Daten, die alle Informationen über den zu Grunde liegenden Prozess enthalten. Die Anzahl der Datenpunkte wird mit vom Curse of Dimensionality und dem zu modellierenden Prozess bestimmt – dabei ist ein Mindestmaß notwendig, um ein valides Modell zu bilden. Ein sehr einfacher Prozess wird nur wenige Punkte benötigen, ein sehr komplexer sehr viele. Um ein ausgewogenes Maß zu finden, sind Data Scientist und Domänenexpert*in aufeinander angewiesen. Aber eine einfache Antwort auf die Frage, wie viele Datenpunkte benötigt werden, gibt es, wie so häufig, nicht.
