
Generative neuronale Modelle haben in Anwendungsbereichen gute Erfolge erzielt, in denen handkuratierte Daten für überwachtes Lernen schwer oder nicht erhältlich sind. Ein häufig genanntes Beispiel ist hier die Erzeugung von „echt“ aussehenden künstlichen Bildern wie zum Beispiel Portraitaufnahmen anhand einer großen Zahl von unklassifizierten Fotos durch Generative Adversarial Networks (GANs). Wir möchten mit diesem Beitrag das allgemeine Prinzip hinter dem generativen Ansatz erklären. Als Beispiel-Architektur wählen wir nicht das GAN, das an sich schon eine komplizierte interne Architektur und einen komplexen Trainingsablauf hat, sondern das einfache Autoencoder Netz, das oft als Komponente für GANs verwendet wird
Was können generative neuronale Modelle besser (als diskriminative Modelle)?
In der statistischen Modellierung wird zwischen diskriminativen und generativen Modellen unterschieden. Bei den maschinellen Lernverfahren kann man diese Unterscheidung so charakterisieren: Diskriminative Modelle definieren ihre Lernleistung ausschließlich in Bezug auf die gewählten Trainingsdaten. Anders formuliert, erzeugt das fertig trainierte Modell eine Ausgabe aus einem nicht zur Trainingsmenge gehörenden Eingabedatum gegeben die Trainingsmenge. Dies beinhaltet einerseits die Aussage, dass zur Berechnung der Ausgabe ausschließlich die aus den Trainingsdaten abgeleiteten Regularitäten verwendet werden. Andererseits fällt damit den Trainingsdaten die Rolle eines absoluten Standards zu. Beispiele sind Klassifikatoren wie Entscheidungsbäume, die (einfache) Support Vector Maschine und neuronale Mehrschichtnetze, die mit Backpropagation und der Standard-Verlustfunktion (MSE = Mean Square Error) trainiert werden.
Demgegenüber beschreibt ein generatives Machine Learning Modell die nicht direkt zugängliche bedingte Wahrscheinlichkeitsverteilung (Bayes Verteilung), die die zum Training verwendeten Eingabe-Ausgabe Paare erzeugt hat. Dieser Ansatz unterscheidet sich in seiner Sichtweise daher grundsätzlich vom diskriminativen Ansatz: Generative Modelle versuchen eine verallgemeinerte Aussage zu treffen über die latenten Wahrscheinlichkeitsverteilungen, die einer beobachtbaren Datenmenge zugrunde liegen. Häufig wird dies auch so formuliert, dass das generative Modell die latente Wahrscheinlichkeitsverteilung (und die daraus resultierenden realen Beobachtungen) rekonstruiert.
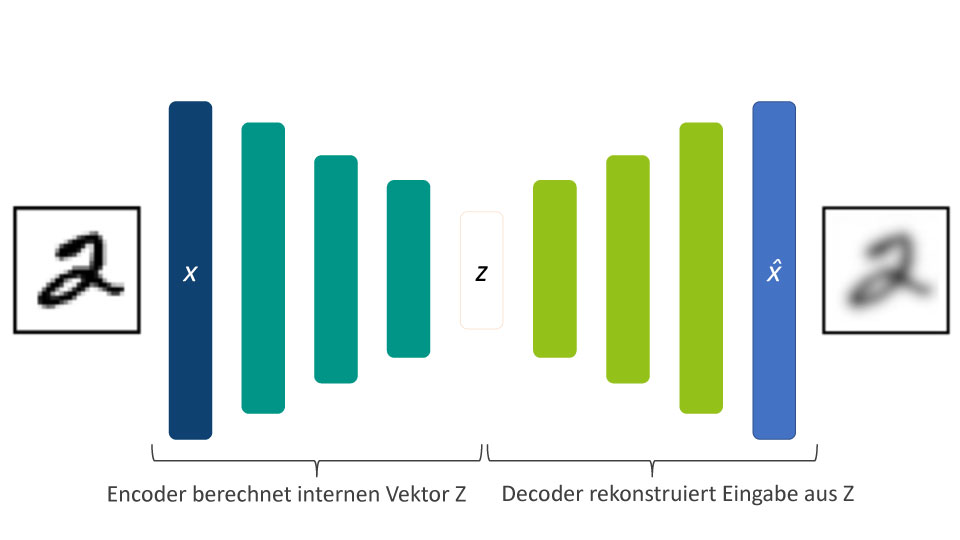
Abbildung 1: Autoencoder Schema
Der wesentliche Aspekt dieses Ansatzes ist die Möglichkeit, mithilfe eines trainierten Modells neue Ausgaben zu erzeugen sowie über das Modell Aussagen über die Ungleichgewichtung von Trainingsdaten zu erhalten. Diese recht abstrakte Charakterisierung können wir uns am Beispiel des Neuronalen Autoencoders in ihren praktischen Auswirkungen besser klarmachen.
Ein diskriminatives Modell: Neuronale Autoencoder
Neuronale Autoencoder sind neuronale Netze mit einer (oder mehreren) internen Schicht(en) von Neuronen, deren Dimension kleiner ist als die Dimension der Eingabevektoren. Die Lernaufgabe besteht darin, in der Ausgabeschicht den Eingabevektor möglichst ohne Abweichungen zu rekonstruieren. Autoencoder wurden ursprünglich dazu entwickelt, um komprimierte, niedrig dimensionale Codierungen von Daten zu erzeugen. (Siehe Abbildung 1) Neuronale Autoencoder sind also nach unserer obigen Beschreibung diskriminative Modelle, die darauf optimiert sind, eine deterministische Abbildung zwischen Eingabe- und Ausgabedaten zu lernen. Welche Änderungen benötigt man nun, um aus einem Autoencoder ein generatives Modell zu erhalten?
Angewendet auf Autoencoder besagt das generative Prinzip, dass der Encoder nicht nur die verfügbaren Daten optimal abbilden, sondern eine latente Wahrscheinlichkeitsverteilung lernen soll, die eigentlich die internen Codierungen des Encoders erzeugt. Hat man so ein Encoder Modell, kann man es nutzen, um unabhängig von den Trainingsdaten neue Codierungen für neue Eingabedaten auf Basis der gelernten Wahrscheinlichkeitsverteilung zu erzeugen. Aufgrund einer großen erzeugten Datenmenge kann man dann abschätzen, wie ungleich gewichtet die ursprünglichen Trainingsbeispiele verteilt sind. Durch eine gezielte andere Auswahl von Teilmengen aus den Trainingsdaten erhält man wiederum eine besser geeignete Trainingsmenge, die auch für andere Lernaufgaben genutzt werden kann.
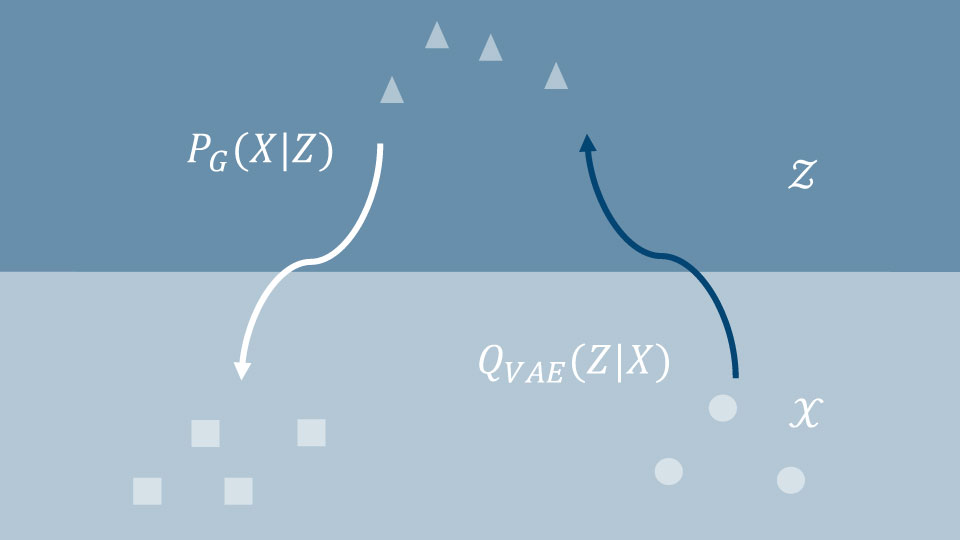
Abbildung 2: Abbildungen zwischen Datenraum und latenter Wahrscheinlichkeitsverteilung
Dies bedeutet, dass wir jetzt den Autoencoder zum Lernen zweier probabilistischer Inferenzfunktionen nutzen wollen: Dies ist in Abbildung 2 grafisch dargestellt (weitere Erläuterungen hierzu siehe den letzten Abschnitt über Wasserstein Autoencoder): Die erste Funktion [latex]Q_{mathrm{VAE}}(Z|X)[/latex] bildet den Eingaberaum [latex]cal(X)[/latex] auf den Raum der latenten Autoencoder Repräsentationen [latex]cal{Z}[/latex] ab. Die zweite Funktion [latex]P_{mathrm{G}}(X|Z)[/latex] bildet den latenten Raum [latex]cal(Z)[/latex] dann auf den Ausgaberaum (der identisch mit dem Eingaberaum ist) ab. Wie dies für Autoencoder auf Basis eines neuronalen Netzes aussieht, ist in Abbildung 3 schematisch dargestellt. Beide Inferenzfunktionen nutzen statt der deterministischen Rechenregel für die Vorwärts-Propagation in neuronalen Netzen eine modifizierte Funktion. Diese berechnet die internen Werte des Autoencoders aus den Eingabewerten unter zusätzlicher Anwendung einer vorher fest definierten Wahrscheinlichkeitsverteilung, die deshalb A-priori-Verteilung genannt wird. Meistens wird dafür eine Gauss-Verteilung genutzt. Dieses theoretische Konzept benötigt für die praktische Umsetzung noch grundlegende Modifikationen, die im Variational Autoencoder realisiert werden.
Ein generatives Modell: Variational Autoencoder
Die Standard-Backpropagation Lernregel des Autoencoders kann nicht auf Zufallsfunktionen angewendet werden. Dieses Problem wird durch eine sogenannte Reparametrisierung aus der Variationsrechnung gelöst. Daher auch der Name Variational Autoencoder. Im Wesentlichen bewirkt die Reparametrisierung der Lernregel, dass die beim Backpropagation Schritt in der internen Schicht des Autoencoders „ankommenden“ deterministischen Gradienten durch Parameter der Zufallsverteilung variiert werden. (siehe Abbildung 4)
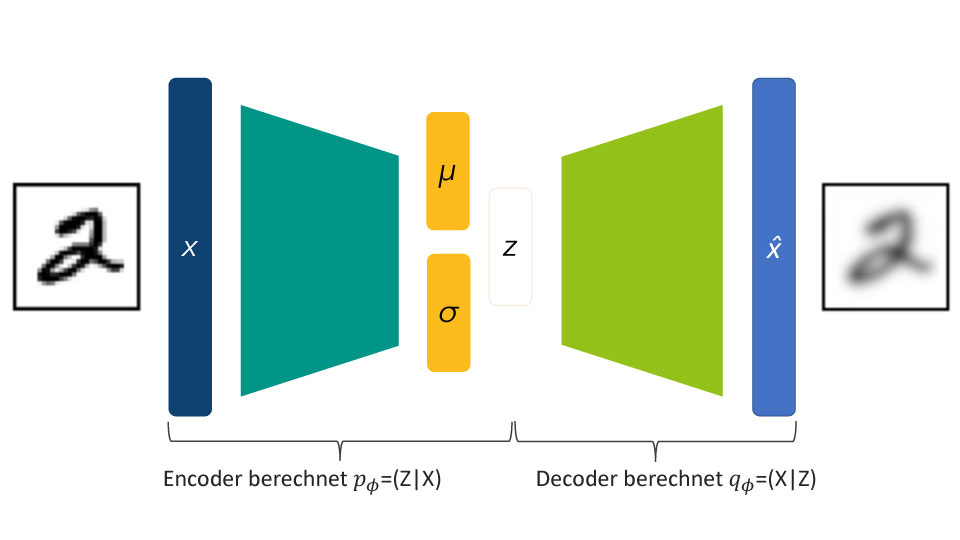
Abbildung 3: Variational Autoencoder Schema
Die Berechnung der Gradienten selbst aus dem Vergleich von errechneter Ausgabe und der Lernvorgabe (die in diesem Fall ja identisch mit der Eingabe ist), muss ebenfalls modifiziert werden. Das bedeutet, dass eine andere Verlustfunktion als die übliche MSE Funktion (= mean squared error) definiert werden muss. Dies ist damit begründet, dass der Autoencoder nicht einfach die deterministische Relation zwischen Eingabe und Ausgabe lernen, sondern die Unterschiede zwischen der Verteilung der errechneten Ausgabe und der Trainingsvorgabe-Verteilung minimiert werden soll. Daher benötigen wir eine Verlustfunktion, deren Gradient auch in den Bereichen des Datenraums definiert ist, für den keine Daten vorliegen und für den die Wahrscheinlichkeiten der Datenverteilung teilweise sehr gering sind.
Für den Vergleich zweier Wahrscheinlichkeitsverteilungen eignen sich aus diesen Gründen sogenannte Divergenz-Maße. Diese sind im Unterschied zu Verlustfunktionen wie MSE nicht direkt über die Fehler definiert, die aus den Ausgaben eines neuronalen Netzes im Vergleich zu den Trainingsvorgaben berechnet werden. Divergenzmaße vergleichen vielmehr die latente Wahrscheinlichkeitsverteilung (die die Trainigsdaten „erzeugt“ hat) mit der durch das gerade lernende Modell erzeugten Wahrscheinlichkeitsverteilung. Daher enthalten die theoretischen Formeln der Divergenzmaße Integrale. In der Praxis können diese Integrale jedoch nicht analytisch berechnet werden, sondern sie werden durch Auswertung der Trainingsdaten und Modellausgaben approximiert. Wir beschreiben im nächsten Abschnitt das Beispiel eines Variational Autoencoders mit der Wasserstein Divergenz als Verlustfunktion.
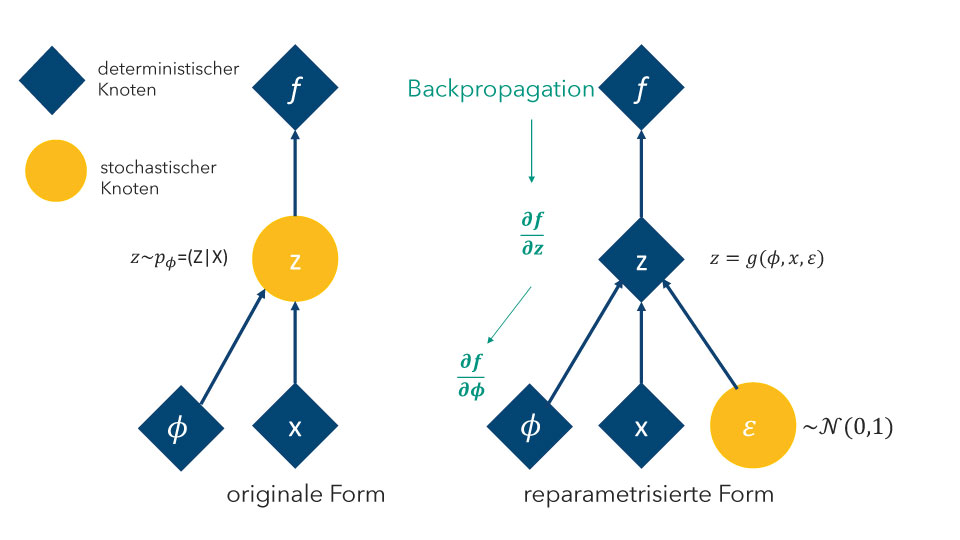
Abbildung 4: Reparametrisierung
Wasserstein Autoencoder
Der konzeptuelle Unterschied zwischen Variational Autoencoders mit Standard-Verlustfunktion und solchen mit Wasserstein Divergenz wird in Abbildung 5 dargestellt. Abbildung 5a visualisiert die Verhältnisse für einen Variational Autoencoder und Abbildung 5b die für einen Wasserstein Autoencoder. Beide Abbildungen sind in eine obere und eine untere Hälfte unterteilt. Die dunkelblaue Hälfte stellt den latenten, nicht beobachtbaren Datenraum dar, in dem die latenten Entsprechungen realer Daten (die „Codes“) als weiße Dreiecke dargestellt sind. Die untere, hellblaue Hälfte stellt den realen Datenraum mit den beobachteten (Trainings-) Daten als Kreise und den Rekonstruktionen des Autoencoders als Quadrat dar.
Zunächst einige Erläuterungen zu den Symbolen in den Abbildungen: [latex]cal{X}[/latex] bezeichnet den realen Datenraum, in dem die beobachteten Daten [latex]X[/latex](die kleinen Kreise) liegen. [latex]cal{Z}[/latex] ist der latente Datenraum, in dem die latenten Codes [latex]Z[/latex] liegen. Die Inferenzfunktion [latex]P_{mathrm{G}}(X|Z)[/latex] „rekonstruiert“ aus den latenten Codes (Dreiecke) reale Daten (Quadrate) aufgrund der erlernten Wahrscheinlichkeitsverteilung [latex]P_Z[/latex]. Die Inferenzfunktionen [latex]Q_{mathrm{VAE}}(Z|X)[/latex] (Abbildung 5a) und [latex]Q_{mathrm{WAE}}(Z|X)[/latex] (Abbildung 5b) bilden die real beobachteten Daten (Kreise) auf die latenten Codes (Dreiecke) ab.
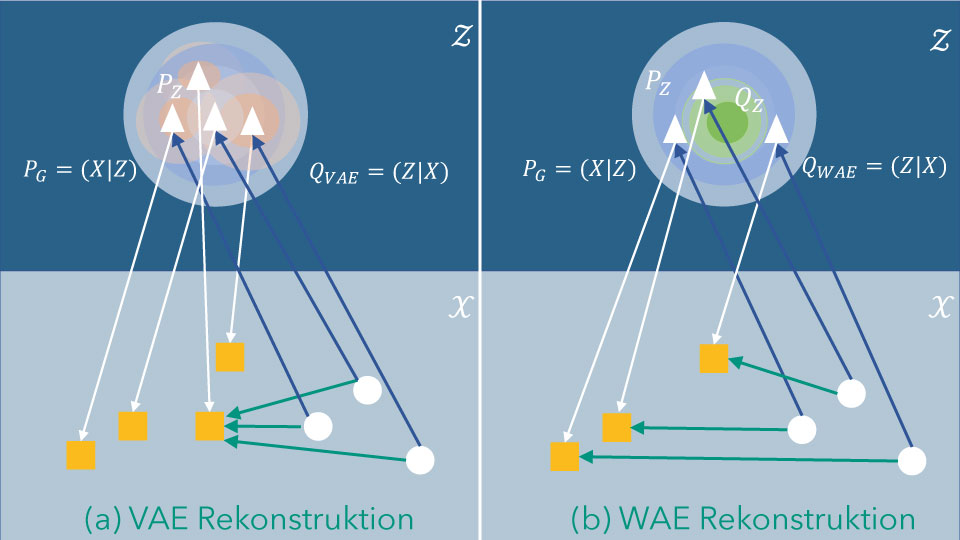
Abbildung 5: Variational (VAE) und Wasserstein (WAE) Autoencoder
Im Falle des VAE in Abbildung 5a führt die Standard-Verlustfunktion beim Lernen dazu, dass unterschiedliche reale Daten [latex]x[/latex] unterschiedliche Inferenzfunktionen [latex]Q_{mathrm{VAE}}(Z|X=x)[/latex] und somit lokale Wahrscheinlichkeitsverteilungen [latex]P_Z[/latex] in [latex]cal{Z}[/latex] induziert werden. In Abbildung 5a ist dies durch mehrere orange Kreise um die latenten Codes angedeutet. Dadurch wird die latente Wahrscheinlichkeitsverteilung [latex]Z[/latex] (weißer Kreis) nur unzureichend approximiert. Dies führt zu ungenauen Rekonstruktionen der realen Daten durch das Autoencoder Modell (grüne Pfeile). Im Gegensatz dazu ermöglicht die Wasserstein Verlustfunktion beim WAE (Abbildung 5b) eine konsistente Approximation [latex]P_Z[/latex] der latenten Verteilung [latex]Q_Z[/latex] und damit können unterschiedliche reale Daten auch in ihren Rekonstruktionen besser unterschieden werden. Mehr Informationen über Wasserstein-Autoencoder kann in dem zugehörigen Paper von Ilya Tolstikhin et al. gefunden werden.
Wir haben in diesem Blog-Beitrag das Prinzip der generativen Modelle am Beispiel des neuronalen Autoencoders skizziert. In praktischen Anwendungen finden sich generative Modelle oft verborgen in komplexen neuronalen oder hybriden Architekturen, wie etwa GANs. Die Erfolge dieses relativ neuen Typs neuronaler Netze im Bereich Bildverarbeitung, autonomer Systeme und neuerdings auch maschineller Übersetzung demonstrieren die Adäquatheit dieses Ansatzes für die Auswertung sehr großer realer Datenmengen mir dem Ziel, allgemeingültige Modelle anzunähern.
