Interpretierbare Wort-Repräsentationen und Themenanalyse mittels Matrix-Faktorisierung

Word-Embeddings spielen eine zentrale Rolle in der maschinellen Analyse von Texten. Ein zentrales Problem der computergesteuerten Analyse von Textdaten ist die Frage, wie man Wörter, die aus reinen Zeichenfolgen bestehen, für Systeme lesbar macht, die meist auf Basis von Zahlenvektoren arbeiten. Zusätzlich beschäftigen sich weitere Forschungsgebiete, so auch im Kompetenzzentrum ML2R, mit der wichtigen Fragestellung zur Interpretierbarkeit der Wort-Repräsentationen. Doch bevor wir unseren entwickelten Ansatz vorstellen, erklären wir einleitend, wie Textdaten im System überhaupt lesbar gemacht werden.

Ein erster Ansatz zur Lösung dieser Herausforderung bilden dabei sogenannte Word-Embeddings, also Vektor-Repräsentationen für Wörter. Word-Embeddings ordnen jedem Wort in einem gegebenen Vokabular einen Vektor einer festgelegten Größe zu, nachdem diese Vektoren auf Trainingsdaten berechnet wurden. Wie nützlich diese Repräsentationen sind, hängt dabei von dem genutzten Algorithmus, den Trainingsdaten, dem Vokabular und der Größe der Vektoren ab. Sobald Word-Embeddings gut trainiert wurden, zeigen sie die interessante Eigenschaft, dass semantische Zusammenhänge zwischen Wörtern auf geometrische Zusammenhänge zwischen den jeweiligen Vektoren übertragen werden. Ein berühmtes Beispiel dafür lässt sich mit word2vec Wort-Embeddings zeigen:

Subtrahiert man den Vektor für ‚Mann‘ vom Ausgangsvektor ‚König‘ und addiert dafür den Vektor für ‚Frau‘, erhält man einen Vektor, der dem Vektor ‚Königin‘ sehr ähnlich ist. Diese Beziehungen zwischen Vektoren ermöglichen es nun, Texte mit Hilfe von selbstlernenden Systemen zu analysieren und Wörter und ganze Paragrafen zu klassifizieren.

Vor- und Nachteile der Word-Embedding Modelle

Die bekanntesten Word-Embedding Modelle (wie GloVe und word2vec) beruhen dabei auf der Matrix-Faktorisierung. Für ein gegebenes Vokabular der Größe [latex]n[/latex] wird dabei aus Trainingsdaten eine Eingabematrix der Größe [latex]ntimes n[/latex] erstellt, die Zusammenhänge zwischen Wörtern im gesamten Textkorpus festhält. In der Eingabematrix wird gezählt, wie oft ein Wort im Zusammenhang mit anderen Wörtern vorkommt (zum Beispiel im gleichen Satz oder in einer festgelegten Umgebung), dies wird auch Kookkurrenz genannt. Anschließend wird diese Matrix in Matrizen von kleinerer Dimensionalität faktorisiert, sodass die Informationen aus der Eingabematrix in kleinere Dimensionen komprimiert werden. Dadurch müssen Beziehungen zwischen Wörtern in die kleineren Repräsentationen miteinfließen. Somit definiert sich die Bedeutung eines Wortes aus den Wörtern, die oft in seiner Umgebung vorkommen – Passend zu dem bekannten Zitat des bekannte Linguisten John Rupert Firth:  „You shall know a word by the company it keeps.“ (1957)

Obwohl Word-Embeddings für viele Aufgaben sehr nützlich sind, weisen sie auch deutliche Nachteile auf: Um die gesamte Information der Trainingsdaten zu repräsentieren, müssen die Vektoren eine bestimmte Größe haben. Gängige Modelle erzeugen Vektoren von einer Länge zwischen 50 und 300 Zahlen. Das bedeutet, dass ein Wort durch bis zu 300 Zahlen repräsentiert wird. Es ist dabei nicht nachvollziehbar, ob einzelne Zahlen verschiedene Eigenschaften des Wortes darstellen oder ob nur die geometrischen Beziehungen der kompletten Vektoren die Repräsentation bestimmen.

Durch die fehlende Nachvollziehbarkeit ist es kaum möglich, ein Modell, das auf Basis dieser Vektoren Text klassifiziert, genauer zu untersuchen.  Wird ein Wort falsch klassifiziert, lässt sich der Fehler eventuell auf einzelne Dimensionen der Eingangsdaten (Wortvektoren) zurückführen. Jedoch sind die einzelnen Dimensionen nicht ohne weiteres interpretierbar, wodurch sich die Analyse nur schwer fortführen lässt.

Interpretierbare DEDICOM Faktorisierung

Deshalb wurde in einer aktuellen Studie von ML2R Wissenschaftler*innen ein Ansatz zur verbesserten Interpretierbarkeit entwickelt: Wortvektoren durch DEDICOM Matrix Faktorisierung. DEDICOM steht für Decomposition into Directed Components und wurde in der Forschung bereits zur Untersuchung von sozialen Netzwerken, E-Mail-Verkehr und Nutzungsverhalten in Computerspielen genutzt. Die Anwendung auf Wortvektoren beschreibt jedoch einen neuen Ansatz.

Doch was ist das Besondere an diesem Ansatz? DEDICOM stellt eine spezielle Art der Faktorisierung einer quadratischen Matrix dar: Eine Eingabematrix $S$ der Größe $n times n$ wird in eine Gewichtsmatrix $A$ der Größe $n times k$ und eine Zusammenhangsmatrix $R$ der Größe $k times k$ geteilt, sodass $S=ARA^T$. Die Eingabematrix $S$, wie in anderen Word-Embedding Algorithmen, bildet eine angepasste Kookkurrenz-Matrix des Trainingskorpus mit der Vokabulargröße $n$.

Die Faktormatrix $A$ gibt dann $k$-dimensionale Wortvektoren aus, wobei im Gegensatz zu anderen Algorithmen $k$ deutlich kleiner gewählt wird. Sortiert man die berechneten Wortvektoren nun absteigend nach ihren einzelnen Komponenten, erhält man Gruppen von Wörtern, die thematisch zusammengehören. Man hat so die wichtigsten Themen des Ausgangstexts extrahiert und kann sie durch die dazugehörigen Wörter identifizieren. Zusätzliche Restriktionen auf dem Faktorisierungsalgorithmus lassen jeden Wortvektor eine Wahrscheinlichkeitsverteilung über die Themen repräsentieren. Das heißt, der dritte Eintrag eines Wortvektors gibt an, mit welcher Wahrscheinlichkeit das Wort dem dritten Thema zuzuordnen ist.

Matrix $R$ zeigt an, welche Themen besonders oft zusammen auftreten. Wählen wir beispielsweise 10 für $k$, gibt die Matrix $R$ dann den Zusammenhang zwischen den 10 Dimensionen (Themen) an: Ein großer Wert in Zeile 3 und Spalte 6 bedeutet, dass Wörter mit viel Gewicht in dem 3-ten und 6-ten Eintrag ihres Vektors oft zusammen im Text auftreten. Dadurch lassen sich die einzelnen Dimensionen als thematische Komponenten des Textkorpus auffassen.

$ARA^T$ repräsentiert die rekonstruierte $S$ Matrix. Je ähnlicher $ARA^T$ zu $S$, desto genauer wurden die Informationen der Eingangsmatrix extrahiert.

DEDICOM Hands-On Beispiel

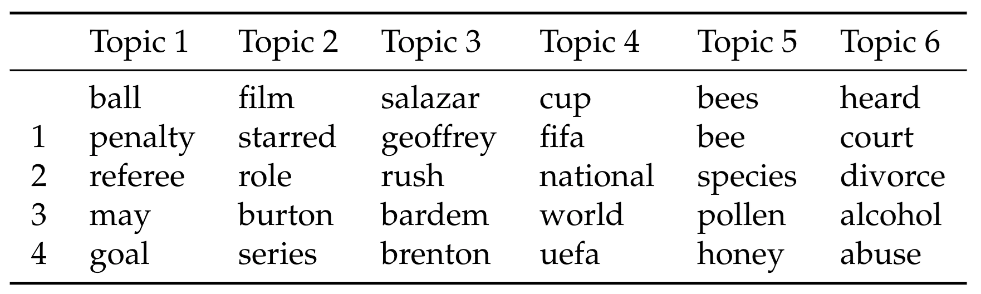
Um die Vorteile der DEDICOM Faktorisierung in der Praxis genauer darzustellen, gehen wir im Folgenden näher auf ein ausgewähltes Beispiel unserer Studie ein. Die Tabelle zeigt die mit DEDICOM extrahierten Themen eines künstlichen Textkorpus, der aus den englischen Wikipedia Artikeln “Johnny Depp”, “Bee” und “Soccer” besteht.

Hierbei lässt sich schnell erkennen, dass sich Themen 1 und 4 eindeutig dem “Soccer” Artikel zuordnen lassen. Während Thema 1 den Fokus auf die Spielmechanik legt, bildet Thema 4 den professionellen beziehungsweise strukturellen Aspekt des Fußballs ab. Schauen wir genau auf das Thema 6, zeigt sich, dass sehr spezifisch das schwierige Verhältnis zwischen Schauspieler Johnny Depp und seiner Ex-Ehefrau Amber Heard aufgegriffen wird.

Nun führen wir die Analyse weitergehend fort: In Tabelle 2 analysieren wir den gelernten Vektorraum, indem wir für das wichtigste Wort eines jeden Themas die vier ähnlichsten Wörter ermitteln. Ähnlichkeit wird hier definiert als die Kosinus-Ähnlichkeit zwischen zwei Wortvektoren. Es lässt sich erkennen, dass unser DEDICOM Algorithmus, ähnlich wie word2vec und GloVe, die semantische Ähnlichkeit zwischen Wörtern wie “film” und “starred” im Thema 2 auch im gelernten Vektorraum enkodiert.

Darüber hinaus ermöglicht DEDICOM die gleichzeitige Extraktion von relevanten Themen und die Generierung von interpretierbaren Wortvektoren aus dem gegebenen Textkorpus: Jeder Eintrag im Vektor zeigt an, mit welcher Wahrscheinlichkeit sich das zugehörige Wort dem entsprechenden Thema des Eintrags zuordnen lässt. Die auf unseren interpretierbaren Wortvektoren aufbauenden Machine-Learning Modelle lassen sich somit einfacher analysieren. Können Fehler in der Klassifizierung auf einzelne Dimensionen der Eingangsdaten zurückgeführt werden, ist eine thematische Interpretation der Klassifizierung möglich.

Wir fassen zusammen: Der DEDICOM Algorithmus eignet sich für die gleichzeitige Extraktion von Themen und die Repräsentation von Wörtern durch interpretierbare Wortvektoren. Letztere können ebenfalls für weitere Machine-Learning-Modelle verwendet werden, um deren Erklärbarkeit zu fördern.

Mehr Informationen zum Algorithmus, ausführliche Experimente und Vergleiche mit anderen Methoden in der zugehörigen Publikation:

Interpretable Topic Extraction and Word Embedding Learning using row-stochastic DEDICOM
L. Hillebrand, D. Biesner, C. Bauckhage, R. Sifa. CD-MAKE, 2020, Link.