
Unvollständige Daten stellen ein immer wieder auftretendes Problem für Maschinelles Lernen dar. Mit Hilfe eines wahrscheinlichkeitsbasierten Verfahrens lassen sich jedoch die Lücken solcher Datensätze schließen, damit sie für weitere Verarbeitung nutzbar sind.
Daten sind im Kontext des Maschinellen Lernens unabdingbar. In vielen Domänen können Datensätze jedoch aufgrund von Fehlern bei der Messung oder Verarbeitung unvollständig sein. Das zeigt sich zum Beispiel auch im UCI Machine Learning Repository, wo zwei der fünf beliebtesten Datensätze fehlende Einträge beinhalten („Adult“ und „Heart Disease“). Bei Daten mit Lücken ist das Lernen von Modellen oft schwierig, und in manchen Fällen sogar unmöglich. Allerdings können generative Verfahren helfen, indem sie unvollständige Daten mit möglichst sinnvollen Annäherungen auffüllen.
Wahrscheinlichkeitsbasierte Modellierung
Die Einträge eines jeden Datensatzes lassen sich als konkrete Realisierungen eines Zufallsvektors interpretieren. Aufgrund der Unvollständigkeit sind dann einzelne Komponenten des Vektors unbeobachtet. Je nach Datensatz können auch bei jedem Eintrag andere Komponenten fehlen. Bei der Modellierung des Zufallsvektors muss man im Allgemeinen auch berücksichtigen, dass einzelne Komponenten statistisch abhängig voneinander sein können. Solche Abhängigkeiten lassen sich gut durch probabilistische graphische Modelle abbilden, zum Beispiel mit Markov Random Fields (MRFs).
Bei MRFs werden die Abhängigkeiten durch einen ungerichteten Graphen beschrieben. Dabei wird vorausgesetzt, dass Realisierungen des Zufallsvektors aus einem diskreten Zustandsraum stammen, sodass manche Datensätze zunächst diskretisiert werden müssen. MRFs ermöglichen, die multivariate Wahrscheinlichkeitsverteilung des Zufallsvektors zu berechnen. Marginalisierung erlaubt zudem, auch die Wahrscheinlichkeit für beliebige bedingte partielle Belegungen zu berechnen. Im Kontext eines unvollständigen Datensatzes kann so die Sinnhaftigkeit verschiedener Vorhersagen für fehlende Einträge untersucht werden. Vorher müssen jedoch im Training die Parameter des MRFs basierend auf verfügbaren Daten bestimmt werden. Klassisch wird dafür eine Maximum-Likelihood-Schätzung durchgeführt, die jedoch vollständig beobachtete Daten benötigt.
Parameterschätzung mit unvollständigen Daten
Das Training eines MRFs ist glücklicherweise auch mit unvollständigen Daten möglich. Dafür führt man die Maximum-Likelihood-Schätzung nach einem Erwartungs-Maximierungs-Schema durch. Im Kern werden also abwechselnd die fehlenden Teile des Datensatzes mithilfe von Sampling aufgefüllt, und anschließend die Parameter neu geschätzt.
Im Falle von extrem großen Lücken im Datensatz kann jedoch die Zufälligkeit des ersten Erwartungs-Schrittes (also zufälliges Samplen aus dem Zustandsraum) die Schätzung der initialen Parameter überschatten. Um dem entgegenzuwirken, kann man statistisches Wissen aus den Daten abzuleiten, und dieses in Form von Regularisierung in die Parameterschätzung einfließen lassen.
Rekonstruktion der Daten
Es stellt sich nun noch die Frage, wie man mithilfe des trainierten MRFs die Lücken im Datensatz mit sinnvollen Werten füllen kann. Das MRF erlaubt uns die Berechnung der Wahrscheinlichkeitsfunktion für bestimmte Belegungen, und somit den Gütevergleich verschiedener Vorhersagen.
Es lässt sich auch eine in der Regel eindeutig wahrscheinlichste Belegung berechnen, der sogenannte Maximum-a-posteriori (MAP) Zustand. Im Falle von unvollständigen Daten wird der MAP Zustand durch die zum Teil vorhandenen Beobachtungen bedingt. Lücken im Datensatz lassen sich also schließen, indem man alle fehlenden Einträge durch die MAP Vorhersage ersetzt. Alternativ kann man mit dem MRF auch die Wahrscheinlichkeit für verschiedene Vorhersagen berechnen, und diese gegebenenfalls kombinieren.
Anwendung im Kontext von Satellitendaten
Satellitenbilder dienen als gutes Beispiel für unvollständige Datensätze. Sie sind seit Jahren fester Bestandteil der Forschung, zum Beispiel in den Bereichen Klimawandel und Untersuchung der Flächennutzung. Jedoch sind große Teile der vom Weltraum erfassten Erdoberfläche von Wolken verdeckt. Dementsprechend spielt bei der Verarbeitung von Satellitendaten das “Gap Filling“ eine wichtige Rolle. In der nachfolgenden Abbildung sieht man, wie mit unserem Ansatz Wolken auf den Bildern entfernt werden können.
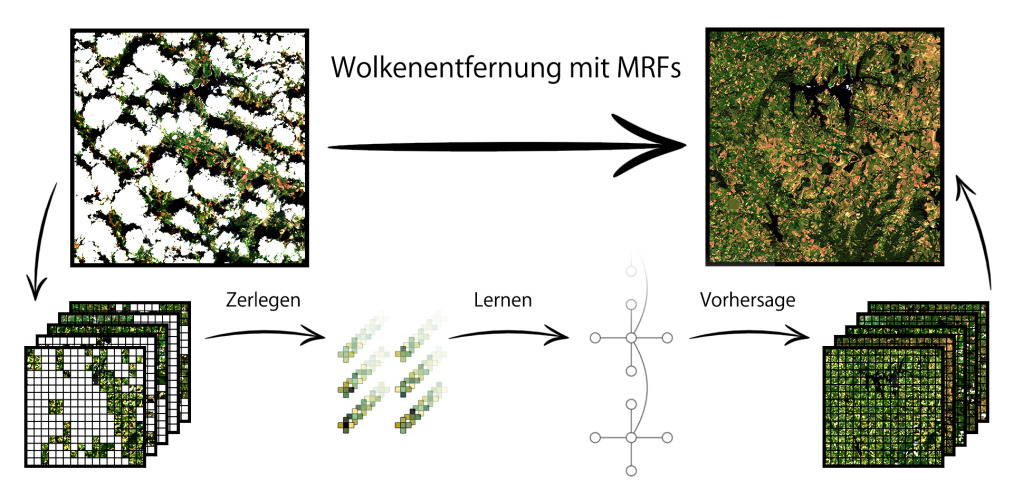
Die Satellitenbilder der zum Teil durch Wolken verdeckten Erdoberfläche können mithilfe wahrscheinlichkeitsbasierter Modellierung rekonstruiert werden.
Wie man sieht, erlauben uns die vorgestellten MRFs, selbst stark bewölkte Aufnahmen zu rekonstruieren. Für die räumlich-zeitlichen Satellitendaten macht es Sinn, lediglich die lokale räumliche Nachbarschaft der einzelnen Pixel zu modellieren, und das fertige Modell für die Aufbereitung über den ganzen Datensatz zu “sliden”. Im Gegensatz zu anderen Methoden ist unser Ansatz nicht auf Zusatzinformationen angewiesen und es werden auch keine Annahmen über die vorliegenden Daten gemacht. Um die Vorhersage bei stark bewölkten Bildern zu verbessern, kann empirisches Vorwissen direkt aus den Daten abgeleitet und beim Training in Form von Regularisierung berücksichtigt werden. In Experimenten sind die MRF-basierten Vorhersagen für bewölkte Teile messbar besser als Rekonstruktionen anderer Ansätze. Dies zeigt sich auch im optischen Vergleich.
Mehr Informationen im zugehörigen Paper:
No Cloud on the Horizon: Probabilistic Gap Filling in Satellite Image Series
Raphael Fischer, Nico Piatkowski, Charlotte Pelletier, Geoffrey Webb, François Petitjean, Katharina Morik. IEEE International Conference on Data Science and Advanced Analytics (DSAA), 2020, PDF.

